Chapter 12.5, Problem 84E

Chebyshev’s Theorem How can you determine whether a distribution is approximately normal? A statistical theorem called Chebyshev’s theorem states that the minimum percent of data between plus and minus K standard deviations from the mean (K > 1) in any distribution can be found by the formula

Minimum percent = $1-\frac{1}{K^2}$

Thus, for example, between ±2 standard deviations from the mean there will always be a minimum of 75% of data. This minimum percent applies to any distribution For K = 2,

Minimum percent $\begin{array}{l}=1-\frac{1}{{-}^2}\\ =1-\frac{1}{4}=\frac{3}{4},\text{or 75\%}\end{array}$

Likewise, between ±3 standard deviations from the mean there will always be a minimum of 89% of the data. For K = 3,

Minimum percent $\begin{array}{l}=1-\frac{1}{3^2}\\ =1-\frac{1}{9}=\frac{8}{9},\text{or 89\%}\end{array}$

The following table lists the minimum percent of data in any distribution and the actual percent of data in the normal distribution between ±1.1, ± 1.5, ± 2.0, and ±2.5 standard deviations from the mean. The minimum percents of data m any distribution were calculated by using Chebyshev’s theorem. The actual percents of data for the normal distribution were calculated by using the area given in the standard normal, or z, table.

	K = 1.1	K = 1.5	K = 2	K = 2.5
Minimum (for any distribution)	17.4%	55.6%	75%	84%
Normal distribution	72.9%	86.6%	95.4%	98.8%
Given distribution

The third row of the chart has been left blank for you to fill in the percents when you reach part (e).

Consider the following 30 pieces of data obtained from a quiz.

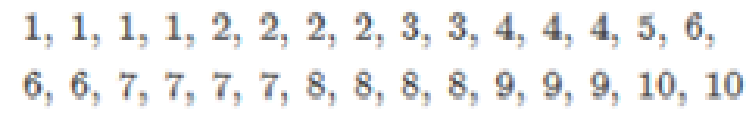
1. a. Determine the mean of the set of scores.
2. b. Determine the standard deviation of the set of scores.
3. c. Determine the values that correspond to 1.1, 1.5, 2, and 2.5 standard deviations above the mean. Then determine the values that correspond to 1.1, 1.5, 2, and 2. 5 standard deviations below the mean.
4. d. By observing the 30 pieces of data, determine the actual percent of quiz scores between

±1.1 standard deviations from the mean.

±1.5 standard deviations from the mean.

±2 tandard deviations from the mean.

±2.5 standard deviations from the mean.

1. e. Place the percents found in part (d) in the third row of the chart.
2. f. Compare the percents in the third row of the chart with the minimum percents in the first row and the normal percents in the second row, and then make a judgment as to whether this set of 30 scores is approximately normally distributed.