Bundle: College Algebra, 7th + WebAssign Printed Access Card for Stewart/Redlin/Watson's College Algebra, 7th Edition, Single-Term
Bundle: College Algebra, 7th + WebAssign Printed Access Card for Stewart/Redlin/Watson's College Algebra, 7th Edition, Single-Term
7th Edition
ISBN: 9781305618152
Author: Lothar Redlin, Saleem Watson, James Stewart
Publisher: CENGAGE C
bartleby

Concept explainers

Unitary Method
The word “unitary” comes from the word “unit”, which means a single and complete entity. In this method, we find the value of a unit product from the given number of products, and then we solve for the other number of products.
Speed, Time, and Distance
Imagine you and 3 of your friends are planning to go to the playground at 6 in the evening. Your house is one mile away from the playground and one of your friends named Jim must start at 5 pm to reach the playground by walk. The other two friends are 3 …
Profit and Loss
The amount earned or lost on the sale of one or more items is referred to as the profit or loss on that item.
Units and Measurements
Measurements and comparisons are the foundation of science and engineering. We, therefore, need rules that tell us how things are measured and compared. For these measurements and comparisons, we perform certain experiments, and we will need the experime…
bartleby

Videos

Textbook Question
Book Icon
Chapter 12.4, Problem 31E

DISCOVER: Amortizing a Mortgage When they bought their house, John and Mary took out a $90,000 mortgage at 9% interest, repayable monthly over 30 years. Their payment is $724.17 per month (check this, using the formula in the text). The bank gave them an amortization schedule, which is a table showing how much of each payment is interest, how much goes toward the principal, and the remaining principal after each payment. The table below shows the first few entries in the amortization schedule.

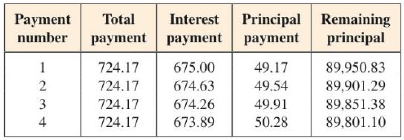
Chapter 12.4, Problem 31E, DISCOVER: Amortizing a Mortgage When they bought their house, John and Mary took out a 90,000

After 10 years they have made 120 payments and are wondering how much they still owe, but they have lost the amortization schedule.

  1. (a) How much do John and Mary still owe on their mortgage? [Hint: The remaining balance is the present value of the 240 remaining payments.]
  2. (b) How much of their next payment is interest, and how much goes toward the principal? [Hint: Since 9% ÷ 12 = 0.75%, they must pay 0.75% of the remaining principal in interest each month.]
Expert Solution & Answer
Check Mark
bartleby

Trending nowThis is a popular solution!

See solution
Check out sample textbook solution
Blurred answer
Previous
Chapter 12.4, Problem 30E
Next
Chapter 12.5, Problem 1E
Students have asked these similar questions
Find the equation of the line / in the figure below. Give exact values using the form y = mx + b. m = b = y WebAssign Plot f(x) = 10* log 9 X
A particle travels along a straight line path given by s=9.5t3-2.2t2-4.5t+9.9 (in meters). What time does it change direction? Report the higher of the answers to the nearest 2 decimal places in seconds.
Use the method of disks to find the volume of the solid that is obtained when the region under the curve y = over the interval [4,17] is rotated about the x-axis.

Chapter 12 Solutions

Bundle: College Algebra, 7th + WebAssign Printed Access Card for Stewart/Redlin/Watson's College Algebra, 7th Edition, Single-Term

Ch. 12.1 - A sequence is a function whose domain is...Ch. 12.1 - Prob. 2ECh. 12.1 - Terms of a Sequence Find the first four terms and...Ch. 12.1 - Prob. 4ECh. 12.1 - Prob. 5ECh. 12.1 - Terms of a Sequence Find the first four terms and...Ch. 12.1 - Prob. 7ECh. 12.1 - Prob. 8ECh. 12.1 - Terms of a Sequence Find the first four terms and...Ch. 12.1 - Prob. 10E
Ch. 12.1 - Prob. 11ECh. 12.1 - Prob. 12ECh. 12.1 - Prob. 13ECh. 12.1 - Prob. 14ECh. 12.1 - Recursive Sequences A sequence is defined...Ch. 12.1 - Recursive Sequences A sequence is defined...Ch. 12.1 - Prob. 17ECh. 12.1 - Prob. 18ECh. 12.1 - Prob. 19ECh. 12.1 - Prob. 20ECh. 12.1 - Prob. 21ECh. 12.1 - Prob. 22ECh. 12.1 - Terms of a Sequence Use a graphing calculator to...Ch. 12.1 - Prob. 24ECh. 12.1 - Prob. 25ECh. 12.1 - Prob. 26ECh. 12.1 - Prob. 27ECh. 12.1 - Prob. 28ECh. 12.1 - nth term of a Sequence Find the nth term of a...Ch. 12.1 - Prob. 30ECh. 12.1 - Prob. 31ECh. 12.1 - Prob. 32ECh. 12.1 - Prob. 33ECh. 12.1 - Prob. 34ECh. 12.1 - Prob. 35ECh. 12.1 - Prob. 36ECh. 12.1 - Prob. 37ECh. 12.1 - Prob. 38ECh. 12.1 - Prob. 39ECh. 12.1 - Prob. 40ECh. 12.1 - Partial Sums Find the first six partial sums S1,...Ch. 12.1 - Prob. 42ECh. 12.1 - nth Partial Sum Find the first four partial sums...Ch. 12.1 - Prob. 44ECh. 12.1 - nth Partial Sum Find the first four partial sums...Ch. 12.1 - nth Partial Sum Find the first four partial sums...Ch. 12.1 - Prob. 47ECh. 12.1 - Prob. 48ECh. 12.1 - Prob. 49ECh. 12.1 - Prob. 50ECh. 12.1 - Prob. 51ECh. 12.1 - Prob. 52ECh. 12.1 - Prob. 53ECh. 12.1 - Prob. 54ECh. 12.1 - Prob. 55ECh. 12.1 - Evaluating a Sum Use a graphing calculator to...Ch. 12.1 - Prob. 57ECh. 12.1 - Prob. 58ECh. 12.1 - Prob. 59ECh. 12.1 - Prob. 60ECh. 12.1 - Prob. 61ECh. 12.1 - Prob. 62ECh. 12.1 - Prob. 63ECh. 12.1 - Prob. 64ECh. 12.1 - Prob. 65ECh. 12.1 - Sigma Notation Write the sum without using sigma...Ch. 12.1 - Sigma Notation Write the sum using sigma notation....Ch. 12.1 - Prob. 68ECh. 12.1 - Prob. 69ECh. 12.1 - Sigma Notation Write the sum using sigma notation....Ch. 12.1 - Sigma Notation Write the sum using sigma notation....Ch. 12.1 - Prob. 72ECh. 12.1 - Prob. 73ECh. 12.1 - Prob. 74ECh. 12.1 - nth Term of a Sequence Find a formula for the nth...Ch. 12.1 - Compound Interest Julio deposits 2000 in a savings...Ch. 12.1 - Prob. 78ECh. 12.1 - Population of a City A city was incorporated in...Ch. 12.1 - Paying off a Debt Margarita borrows 10,000 from...Ch. 12.1 - Fish Farming A fish farmer has 5000 catfish in his...Ch. 12.1 - Prob. 82ECh. 12.1 - Prob. 83ECh. 12.1 - Concentration of a Solution A biologist is trying...Ch. 12.1 - Prob. 85ECh. 12.1 - DISCOVER PROVE: Different Sequences That Start the...Ch. 12.1 - Prob. 87ECh. 12.1 - Prob. 88ECh. 12.2 - An arithmetic sequence is a sequence in which the...Ch. 12.2 - Prob. 2ECh. 12.2 - Prob. 3ECh. 12.2 - Prob. 4ECh. 12.2 - Prob. 5ECh. 12.2 - Prob. 6ECh. 12.2 - Prob. 7ECh. 12.2 - Prob. 8ECh. 12.2 - Prob. 9ECh. 12.2 - Prob. 10ECh. 12.2 - Prob. 11ECh. 12.2 - Prob. 12ECh. 12.2 - Prob. 13ECh. 12.2 - Prob. 14ECh. 12.2 - Prob. 15ECh. 12.2 - Prob. 16ECh. 12.2 - Prob. 17ECh. 12.2 - Prob. 18ECh. 12.2 - Prob. 19ECh. 12.2 - Prob. 20ECh. 12.2 - Prob. 21ECh. 12.2 - Prob. 22ECh. 12.2 - Prob. 23ECh. 12.2 - Prob. 24ECh. 12.2 - Prob. 25ECh. 12.2 - Prob. 26ECh. 12.2 - Prob. 27ECh. 12.2 - Arithmetic Sequence? Find the first five terms of...Ch. 12.2 - Arithmetic Sequence? Find the first five terms of...Ch. 12.2 - Prob. 30ECh. 12.2 - Prob. 31ECh. 12.2 - Prob. 32ECh. 12.2 - Prob. 33ECh. 12.2 - Terms of an Arithmetic Sequence Determine the...Ch. 12.2 - Prob. 35ECh. 12.2 - Prob. 36ECh. 12.2 - Prob. 37ECh. 12.2 - Prob. 38ECh. 12.2 - Terms of an Arithmetic Sequence Determine the...Ch. 12.2 - Terms of an Arithmetic Sequence Determine the...Ch. 12.2 - Terms of an Arithmetic Sequence Determine the...Ch. 12.2 - Terms of an Arithmetic Sequence Determine the...Ch. 12.2 - Terms of an Arithmetic Sequence Determine the...Ch. 12.2 - Prob. 44ECh. 12.2 - Finding Terms of an Arithmetic Sequence Find the...Ch. 12.2 - Prob. 46ECh. 12.2 - Prob. 47ECh. 12.2 - Finding Terms of an Arithmetic Sequence Find the...Ch. 12.2 - Prob. 49ECh. 12.2 - Prob. 50ECh. 12.2 - Prob. 51ECh. 12.2 - Prob. 52ECh. 12.2 - Prob. 53ECh. 12.2 - Prob. 54ECh. 12.2 - Prob. 55ECh. 12.2 - Partial Sums of an Arithmetic Sequence Find the...Ch. 12.2 - Prob. 57ECh. 12.2 - Prob. 58ECh. 12.2 - Prob. 59ECh. 12.2 - Prob. 60ECh. 12.2 - Prob. 61ECh. 12.2 - Prob. 62ECh. 12.2 - Prob. 63ECh. 12.2 - Prob. 64ECh. 12.2 - Prob. 65ECh. 12.2 - Prob. 66ECh. 12.2 - Prob. 67ECh. 12.2 - Prob. 68ECh. 12.2 - Prob. 69ECh. 12.2 - Prob. 70ECh. 12.2 - Depreciation The purchase value of an office...Ch. 12.2 - Poles in a Pile Telephone poles are being stored...Ch. 12.2 - Salary Increases A man gets a job with a salary of...Ch. 12.2 - Drive-In Theater A drive-in theater has spaces for...Ch. 12.2 - Theater Seating An architect designs a theater...Ch. 12.2 - Prob. 76ECh. 12.2 - The Twelve Days of Christmas In the well-known...Ch. 12.2 - DISCUSS: Arithmetic Means The arithmetic mean (or...Ch. 12.3 - A geometric sequence is a sequence in which the...Ch. 12.3 - Prob. 2ECh. 12.3 - True or False? If we know the first and second...Ch. 12.3 - Prob. 4ECh. 12.3 - Prob. 5ECh. 12.3 - Prob. 6ECh. 12.3 - Prob. 7ECh. 12.3 - Prob. 8ECh. 12.3 - Prob. 9ECh. 12.3 - Prob. 10ECh. 12.3 - nth Term of a Geometric Sequence Find the nth term...Ch. 12.3 - Prob. 12ECh. 12.3 - Prob. 13ECh. 12.3 - Prob. 14ECh. 12.3 - Prob. 15ECh. 12.3 - Prob. 16ECh. 12.3 - Prob. 17ECh. 12.3 - Prob. 18ECh. 12.3 - Prob. 19ECh. 12.3 - Prob. 20ECh. 12.3 - Geometric Sequence? The first four terms of a...Ch. 12.3 - Prob. 22ECh. 12.3 - Prob. 23ECh. 12.3 - Prob. 24ECh. 12.3 - Prob. 25ECh. 12.3 - Prob. 26ECh. 12.3 - Prob. 27ECh. 12.3 - Prob. 28ECh. 12.3 - Prob. 29ECh. 12.3 - Prob. 30ECh. 12.3 - Prob. 31ECh. 12.3 - Prob. 32ECh. 12.3 - Prob. 33ECh. 12.3 - Prob. 34ECh. 12.3 - Terms of a Geometric Sequence Determine the common...Ch. 12.3 - Prob. 36ECh. 12.3 - Prob. 37ECh. 12.3 - Terms of a Geometric Sequence Determine the common...Ch. 12.3 - Finding Terms of a Geometric Sequence Find the...Ch. 12.3 - Prob. 40ECh. 12.3 - Prob. 41ECh. 12.3 - Finding Terms of a Geometric Sequence Find the...Ch. 12.3 - Prob. 43ECh. 12.3 - Prob. 44ECh. 12.3 - Finding Terms of a Geometric Sequence Find the...Ch. 12.3 - Prob. 46ECh. 12.3 - Which Term? The first term of a geometric sequence...Ch. 12.3 - Prob. 48ECh. 12.3 - Prob. 49ECh. 12.3 - Prob. 50ECh. 12.3 - Prob. 51ECh. 12.3 - Prob. 52ECh. 12.3 - Prob. 53ECh. 12.3 - Prob. 54ECh. 12.3 - Prob. 55ECh. 12.3 - Prob. 56ECh. 12.3 - Prob. 57ECh. 12.3 - Prob. 58ECh. 12.3 - Prob. 59ECh. 12.3 - Prob. 60ECh. 12.3 - Prob. 61ECh. 12.3 - Prob. 62ECh. 12.3 - Prob. 63ECh. 12.3 - Prob. 64ECh. 12.3 - Infinite Geometric Series Determine whether the...Ch. 12.3 - Prob. 66ECh. 12.3 - Prob. 67ECh. 12.3 - Infinite Geometric Series Determine whether the...Ch. 12.3 - Prob. 69ECh. 12.3 - Prob. 70ECh. 12.3 - Prob. 71ECh. 12.3 - Prob. 72ECh. 12.3 - Prob. 73ECh. 12.3 - Prob. 74ECh. 12.3 - Prob. 75ECh. 12.3 - Prob. 76ECh. 12.3 - Prob. 77ECh. 12.3 - Prob. 78ECh. 12.3 - Prob. 79ECh. 12.3 - Prob. 80ECh. 12.3 - Prob. 81ECh. 12.3 - Prob. 82ECh. 12.3 - Prob. 83ECh. 12.3 - Prob. 84ECh. 12.3 - Prob. 85ECh. 12.3 - Prob. 86ECh. 12.3 - Depreciation A construction company purchases a...Ch. 12.3 - Prob. 88ECh. 12.3 - Bouncing Ball A ball is dropped from a height of...Ch. 12.3 - Bacteria Culture A culture initially has 5000...Ch. 12.3 - Mixing Coolant A truck radiator holds 5 gal and is...Ch. 12.3 - Musical Frequencies The frequencies of musical...Ch. 12.3 - Bouncing Ball A ball is dropped from a height of 9...Ch. 12.3 - Prob. 94ECh. 12.3 - St. Ives The following is a well-known childrens...Ch. 12.3 - Prob. 96ECh. 12.3 - Bouncing Ball A certain ball rebounds to half the...Ch. 12.3 - Prob. 98ECh. 12.3 - Geometry A circular disk of radius R is cut out of...Ch. 12.3 - Prob. 102ECh. 12.3 - PROVE: Logarithms of a Geometric Sequence If a1,...Ch. 12.3 - Prob. 104ECh. 12.3 - Geometry A yellow square of side 1 is divided into...Ch. 12.4 - An annuity is a sum of money that is paid in...Ch. 12.4 - Prob. 2ECh. 12.4 - Prob. 3ECh. 12.4 - Annuity Find the amount of an annuity that...Ch. 12.4 - Annuity Find the amount of an annuity that...Ch. 12.4 - Prob. 6ECh. 12.4 - Prob. 7ECh. 12.4 - Prob. 8ECh. 12.4 - Prob. 9ECh. 12.4 - Saving How much money should be invested monthly...Ch. 12.4 - Prob. 11ECh. 12.4 - Prob. 12ECh. 12.4 - Prob. 13ECh. 12.4 - Funding an Annuity A 55-year-old man deposits...Ch. 12.4 - Prob. 15ECh. 12.4 - Prob. 16ECh. 12.4 - Prob. 17ECh. 12.4 - Prob. 18ECh. 12.4 - Mortgage Dr. Gupta is considering a 30-year...Ch. 12.4 - Prob. 20ECh. 12.4 - Prob. 21ECh. 12.4 - Prob. 22ECh. 12.4 - Prob. 23ECh. 12.4 - Prob. 24ECh. 12.4 - Interest Rate John buys a stereo system for 640....Ch. 12.4 - Prob. 26ECh. 12.4 - Prob. 27ECh. 12.4 - Interest Rate A man purchases a 2000 diamond ring...Ch. 12.4 - Prob. 29ECh. 12.4 - Prob. 30ECh. 12.4 - DISCOVER: Amortizing a Mortgage When they bought...Ch. 12.5 - Mathematical induction is a method of proving that...Ch. 12.5 - Prob. 2ECh. 12.5 - Prob. 3ECh. 12.5 - Prob. 4ECh. 12.5 - Prob. 5ECh. 12.5 - Prob. 6ECh. 12.5 - Prob. 7ECh. 12.5 - Prob. 8ECh. 12.5 - Prob. 9ECh. 12.5 - Proving a Formula Use mathematical induction to...Ch. 12.5 - Prob. 11ECh. 12.5 - Proving a Formula Use mathematical induction to...Ch. 12.5 - Prob. 13ECh. 12.5 - Prob. 14ECh. 12.5 - Prob. 15ECh. 12.5 - Prob. 16ECh. 12.5 - Proving a Statement Use mathematical induction to...Ch. 12.5 - Proving a Statement Use mathematical induction to...Ch. 12.5 - Prob. 19ECh. 12.5 - Prob. 20ECh. 12.5 - Prob. 21ECh. 12.5 - Prob. 22ECh. 12.5 - Prob. 23ECh. 12.5 - Prob. 24ECh. 12.5 - Prob. 25ECh. 12.5 - Formula for a Recursive Sequence A sequence is...Ch. 12.5 - Prob. 27ECh. 12.5 - Prob. 28ECh. 12.5 - Prob. 29ECh. 12.5 - Prob. 30ECh. 12.5 - Fibonacci Sequence Fn denotes the nth term of the...Ch. 12.5 - Prob. 32ECh. 12.5 - Prob. 33ECh. 12.5 - Prob. 34ECh. 12.5 - Prob. 35ECh. 12.5 - Prob. 36ECh. 12.5 - Prob. 37ECh. 12.5 - DISCUSS: All Cats Are Black? What is wrong with...Ch. 12.6 - An algebraic expression of the form a + b, which...Ch. 12.6 - Prob. 2ECh. 12.6 - The binomial coefficients can be calculated...Ch. 12.6 - Prob. 4ECh. 12.6 - Prob. 5ECh. 12.6 - Prob. 6ECh. 12.6 - Prob. 7ECh. 12.6 - Prob. 8ECh. 12.6 - Prob. 9ECh. 12.6 - Prob. 10ECh. 12.6 - Prob. 11ECh. 12.6 - Prob. 12ECh. 12.6 - Prob. 13ECh. 12.6 - Prob. 14ECh. 12.6 - Prob. 15ECh. 12.6 - Prob. 16ECh. 12.6 - Prob. 17ECh. 12.6 - Prob. 18ECh. 12.6 - Calculating Binomial Coefficients Evaluate the...Ch. 12.6 - Prob. 20ECh. 12.6 - Prob. 21ECh. 12.6 - Prob. 22ECh. 12.6 - Prob. 23ECh. 12.6 - Prob. 24ECh. 12.6 - Prob. 25ECh. 12.6 - Prob. 26ECh. 12.6 - Prob. 27ECh. 12.6 - Binomial Theorem Use the Binomial Theorem to...Ch. 12.6 - Prob. 29ECh. 12.6 - Prob. 30ECh. 12.6 - Prob. 31ECh. 12.6 - Prob. 32ECh. 12.6 - Prob. 33ECh. 12.6 - Prob. 34ECh. 12.6 - Terms of a Binomial Expansion Find the indicated...Ch. 12.6 - Terms of a Binomial Expansion Find the indicated...Ch. 12.6 - Prob. 37ECh. 12.6 - Prob. 38ECh. 12.6 - Prob. 39ECh. 12.6 - Prob. 40ECh. 12.6 - Prob. 41ECh. 12.6 - Prob. 42ECh. 12.6 - Prob. 43ECh. 12.6 - Prob. 44ECh. 12.6 - Prob. 45ECh. 12.6 - Prob. 46ECh. 12.6 - Prob. 47ECh. 12.6 - Simplifying a Difference Quotient Simplify using...Ch. 12.6 - Prob. 49ECh. 12.6 - Prob. 50ECh. 12.6 - Prob. 51ECh. 12.6 - Prob. 52ECh. 12.6 - Prob. 53ECh. 12.6 - Prob. 54ECh. 12.6 - Difference in Volumes of Cubes The volume of a...Ch. 12.6 - Probability of Hitting a Target The probability...Ch. 12.6 - Prob. 57ECh. 12.6 - Prob. 58ECh. 12.6 - Prob. 59ECh. 12 - (a) What is a sequence? What notation do we use to...Ch. 12 - Prob. 2RCCCh. 12 - Prob. 3RCCCh. 12 - Prob. 4RCCCh. 12 - Prob. 5RCCCh. 12 - Prob. 6RCCCh. 12 - (a) Write 13 + 23 + 33 + 43 + 53 using sigma...Ch. 12 - Prob. 8RCCCh. 12 - Prob. 9RCCCh. 12 - Prob. 10RCCCh. 12 - Prob. 11RCCCh. 12 - Prob. 12RCCCh. 12 - Prob. 1RECh. 12 - Prob. 2RECh. 12 - Prob. 3RECh. 12 - Prob. 4RECh. 12 - Prob. 5RECh. 12 - Prob. 6RECh. 12 - Prob. 7RECh. 12 - Prob. 8RECh. 12 - Prob. 9RECh. 12 - Prob. 10RECh. 12 - Prob. 11RECh. 12 - Prob. 12RECh. 12 - Prob. 13RECh. 12 - Prob. 14RECh. 12 - Prob. 15RECh. 12 - Arithmetic or Geometric? The first four terms of a...Ch. 12 - Prob. 17RECh. 12 - Prob. 18RECh. 12 - Prob. 19RECh. 12 - Prob. 20RECh. 12 - Prob. 21RECh. 12 - Prob. 22RECh. 12 - Prob. 23RECh. 12 - nth Term of a Geometric Sequence Find the nth term...Ch. 12 - Prob. 25RECh. 12 - Prob. 26RECh. 12 - Prob. 27RECh. 12 - Prob. 28RECh. 12 - Salary A teacher makes 32,000 in his first year at...Ch. 12 - Prob. 30RECh. 12 - Prob. 31RECh. 12 - Prob. 32RECh. 12 - Prob. 33RECh. 12 - Prob. 34RECh. 12 - Prob. 35RECh. 12 - Prob. 36RECh. 12 - Prob. 37RECh. 12 - Prob. 38RECh. 12 - Prob. 39RECh. 12 - Prob. 40RECh. 12 - Prob. 41RECh. 12 - Sigma Notation Write the sum without using sigma...Ch. 12 - Prob. 43RECh. 12 - Prob. 44RECh. 12 - Prob. 45RECh. 12 - Prob. 46RECh. 12 - Prob. 47RECh. 12 - Prob. 48RECh. 12 - Prob. 49RECh. 12 - Sums of Arithmetic and Geometric Sequences...Ch. 12 - Prob. 51RECh. 12 - Prob. 52RECh. 12 - Prob. 53RECh. 12 - Prob. 54RECh. 12 - Prob. 55RECh. 12 - Prob. 56RECh. 12 - Prob. 57RECh. 12 - Prob. 58RECh. 12 - Infinite Geometric Series Determine whether the...Ch. 12 - Prob. 60RECh. 12 - Terms of an Arithmetic Sequence The first term of...Ch. 12 - Prob. 62RECh. 12 - Ancestors A person has two parents, four...Ch. 12 - Prob. 64RECh. 12 - Prob. 65RECh. 12 - Prob. 66RECh. 12 - Prob. 67RECh. 12 - Prob. 68RECh. 12 - Prob. 69RECh. 12 - Prob. 70RECh. 12 - Prob. 71RECh. 12 - Prob. 72RECh. 12 - Prob. 73RECh. 12 - Prob. 74RECh. 12 - Prob. 75RECh. 12 - Prob. 76RECh. 12 - Prob. 77RECh. 12 - Prob. 78RECh. 12 - Prob. 79RECh. 12 - Prob. 80RECh. 12 - Prob. 81RECh. 12 - Prob. 82RECh. 12 - Prob. 83RECh. 12 - Prob. 1TCh. 12 - Prob. 2TCh. 12 - Prob. 3TCh. 12 - A geometric sequence begins 12,3,34,316,364,. (a)...Ch. 12 - The first term of a geometric sequence is 25, and...Ch. 12 - The first term of an arithmetic sequence is 10,...Ch. 12 - Prob. 7TCh. 12 - Write the expression without using sigma notation,...Ch. 12 - Prob. 9TCh. 12 - Prob. 11TCh. 12 - Prob. 12TCh. 12 - A puppy weighs 0.85 lb at birth, and each week he...Ch. 12 - Prob. 1PCh. 12 - Fitness Program Sheila decides to embark on a...Ch. 12 - Monthly Savings Program Alice opens a savings...Ch. 12 - Prob. 4PCh. 12 - Prob. 5P
Knowledge Booster
Background pattern image
Calculus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
  • Text book image
    College Algebra
    Algebra
    ISBN:9781305115545
    Author:James Stewart, Lothar Redlin, Saleem Watson
    Publisher:Cengage Learning
    Text book image
    College Algebra
    Algebra
    ISBN:9781938168383
    Author:Jay Abramson
    Publisher:OpenStax
Text book image
College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Text book image
College Algebra
Algebra
ISBN:9781938168383
Author:Jay Abramson
Publisher:OpenStax
SEE MORE TEXTBOOKS
Use of ALGEBRA in REAL LIFE; Author: Fast and Easy Maths !;https://www.youtube.com/watch?v=9_PbWFpvkDc;License: Standard YouTube License, CC-BY
Compound Interest Formula Explained, Investment, Monthly & Continuously, Word Problems, Algebra; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=P182Abv3fOk;License: Standard YouTube License, CC-BY
Applications of Algebra (Digit, Age, Work, Clock, Mixture and Rate Problems); Author: EngineerProf PH;https://www.youtube.com/watch?v=Y8aJ_wYCS2g;License: Standard YouTube License, CC-BY