
Concept explainers
a.
To state: The hypothesis.
a.
Answer to Problem 15E
The hypothesis for interaction is,
The hypothesis for age of salespersonis,
The hypothesis for product is,
Explanation of Solution
Given info:
The table shows age of the sales representative and type of item affect monthly sales.
Calculation:
The hypothesis for interaction is,
Null hypothesis:
Alternative hypothesis:
The hypothesis for age of salesperson is,
Null hypothesis:
Alternative hypothesis:
The hypothesis for productis,
Null hypothesis:
Alternative hypothesis:
b.
To find: The critical value for each F test.
b.
Answer to Problem 15E
The critical F-value of A is 4.26.
The critical F-value of B and
Explanation of Solution
Given info:
The level of significance is 0.05.
Calculation:
Consider factors A represent the type of paintand B represents the geographic location.
Here,
The formula to find the degrees of freedom for factor A is,
Thus, the degrees of freedom for factor A is1.
Here,
The formula to find the degrees of freedom for factor B is,
Thus, the degrees of freedom for factor B is3.
The formula to find the degrees of freedom for factor
Thus, the degrees of freedom for factor
The degrees of freedom for the within (error) factor
The degrees of freedom for the within (error) factor is 24.
Critical value:
Here A having 1 degrees of freedom and B and
For A:
The critical F-value of A is obtained using the Table H: The F-Distribution with the level of significance
Procedure:
- Locate 24 in the degrees of freedom, denominator row of the Table H.
- Obtain the value in the corresponding degrees of freedom, numerator column below 1.
That is,
Thus, the critical F-value of A is 4.26.
For B and
The critical F-value of B and
Procedure:
- Locate 24 in the degrees of freedom, denominator row of the Table H.
- Obtain the value in the corresponding degrees of freedom, numerator column below 2.
That is,
Thus, the critical F-value of B and
Decision criteria:
If
If
If
c.
To compute: The summary table.
To find: The test value.
c.
Answer to Problem 15E
The summary table is,
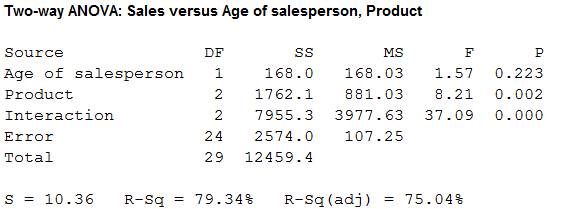
The test valuesare 1.57, 8.21 and 37.09.
Explanation of Solution
Calculation:
Software procedure:
Step-by-step procedure to obtain the test statistics and P-value using the MINITAB software:
- Choose Stat > ANOVA > Two-Way.
- In Response, enter the column of Sales.
- In Row Factor, enter the column of Ages of sales person.
- In Column Factor, enter the column of product.
- Click OK.
Output using the MINITAB software is given below:

From Minitab output, the test valuesare 1.57, 8.21 and 37.09.
d.
To make: The decision.
d.
Answer to Problem 15E
The null hypothesis is rejected for
Explanation of Solution
Conclusion:
From the result of part (c), the
Decision for
Here, the test value of
That is,
Thus, it can be concluding that, the null hypothesis for
Decision for
Here, the test value of
That is,
Thus, it can be concluding that, the null hypothesis for
Decision for
Here, the test value of
That is,
Thus, it can be concluding that, the null hypothesis for
e.
To explain: The results.
e.
Answer to Problem 15E
The result concludes that, there is an interception effect between the ages of salespeople and the type of products sold.
Explanation of Solution
Calculation:
From the results, it can be observed there is a significant between the ages of the sales people and the products they sell on the monthly sales.
Here, the integration effect is between the ages of the sales person and the type of product sold. So, the procedure for drawing the graph for the interaction plot is given below.
Minitab Procedure:
- Choose Stat > ANOVA >Interaction Plot.
- In Response, enter the column of Sales.
- In Factors, enter the column of Ages of sales person and product.
- Click OK.
Output using the MINITAB software is given below:
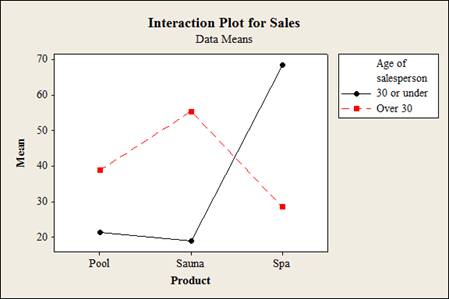
Interpretation:
From the graph, it can be observed that the lines cross. So, the interaction is disordinal interaction. Hence there is an interception effect between the ages of salespeople and the type of products sold.
Want to see more full solutions like this?
Chapter 12 Solutions
ALEKS 360 ELEM STATISTICS
- Q.2.4 There are twelve (12) teams participating in a pub quiz. What is the probability of correctly predicting the top three teams at the end of the competition, in the correct order? Give your final answer as a fraction in its simplest form.arrow_forwardThe table below indicates the number of years of experience of a sample of employees who work on a particular production line and the corresponding number of units of a good that each employee produced last month. Years of Experience (x) Number of Goods (y) 11 63 5 57 1 48 4 54 5 45 3 51 Q.1.1 By completing the table below and then applying the relevant formulae, determine the line of best fit for this bivariate data set. Do NOT change the units for the variables. X y X2 xy Ex= Ey= EX2 EXY= Q.1.2 Estimate the number of units of the good that would have been produced last month by an employee with 8 years of experience. Q.1.3 Using your calculator, determine the coefficient of correlation for the data set. Interpret your answer. Q.1.4 Compute the coefficient of determination for the data set. Interpret your answer.arrow_forwardCan you answer this question for mearrow_forward
- Techniques QUAT6221 2025 PT B... TM Tabudi Maphoru Activities Assessments Class Progress lIE Library • Help v The table below shows the prices (R) and quantities (kg) of rice, meat and potatoes items bought during 2013 and 2014: 2013 2014 P1Qo PoQo Q1Po P1Q1 Price Ро Quantity Qo Price P1 Quantity Q1 Rice 7 80 6 70 480 560 490 420 Meat 30 50 35 60 1 750 1 500 1 800 2 100 Potatoes 3 100 3 100 300 300 300 300 TOTAL 40 230 44 230 2 530 2 360 2 590 2 820 Instructions: 1 Corall dawn to tha bottom of thir ceraan urina se se tha haca nariad in archerca antarand cubmit Q Search ENG US 口X 2025/05arrow_forwardThe table below indicates the number of years of experience of a sample of employees who work on a particular production line and the corresponding number of units of a good that each employee produced last month. Years of Experience (x) Number of Goods (y) 11 63 5 57 1 48 4 54 45 3 51 Q.1.1 By completing the table below and then applying the relevant formulae, determine the line of best fit for this bivariate data set. Do NOT change the units for the variables. X y X2 xy Ex= Ey= EX2 EXY= Q.1.2 Estimate the number of units of the good that would have been produced last month by an employee with 8 years of experience. Q.1.3 Using your calculator, determine the coefficient of correlation for the data set. Interpret your answer. Q.1.4 Compute the coefficient of determination for the data set. Interpret your answer.arrow_forwardQ.3.2 A sample of consumers was asked to name their favourite fruit. The results regarding the popularity of the different fruits are given in the following table. Type of Fruit Number of Consumers Banana 25 Apple 20 Orange 5 TOTAL 50 Draw a bar chart to graphically illustrate the results given in the table.arrow_forward
- Q.2.3 The probability that a randomly selected employee of Company Z is female is 0.75. The probability that an employee of the same company works in the Production department, given that the employee is female, is 0.25. What is the probability that a randomly selected employee of the company will be female and will work in the Production department? Q.2.4 There are twelve (12) teams participating in a pub quiz. What is the probability of correctly predicting the top three teams at the end of the competition, in the correct order? Give your final answer as a fraction in its simplest form.arrow_forwardQ.2.1 A bag contains 13 red and 9 green marbles. You are asked to select two (2) marbles from the bag. The first marble selected will not be placed back into the bag. Q.2.1.1 Construct a probability tree to indicate the various possible outcomes and their probabilities (as fractions). Q.2.1.2 What is the probability that the two selected marbles will be the same colour? Q.2.2 The following contingency table gives the results of a sample survey of South African male and female respondents with regard to their preferred brand of sports watch: PREFERRED BRAND OF SPORTS WATCH Samsung Apple Garmin TOTAL No. of Females 30 100 40 170 No. of Males 75 125 80 280 TOTAL 105 225 120 450 Q.2.2.1 What is the probability of randomly selecting a respondent from the sample who prefers Garmin? Q.2.2.2 What is the probability of randomly selecting a respondent from the sample who is not female? Q.2.2.3 What is the probability of randomly…arrow_forwardTest the claim that a student's pulse rate is different when taking a quiz than attending a regular class. The mean pulse rate difference is 2.7 with 10 students. Use a significance level of 0.005. Pulse rate difference(Quiz - Lecture) 2 -1 5 -8 1 20 15 -4 9 -12arrow_forward
- The following ordered data list shows the data speeds for cell phones used by a telephone company at an airport: A. Calculate the Measures of Central Tendency from the ungrouped data list. B. Group the data in an appropriate frequency table. C. Calculate the Measures of Central Tendency using the table in point B. D. Are there differences in the measurements obtained in A and C? Why (give at least one justified reason)? I leave the answers to A and B to resolve the remaining two. 0.8 1.4 1.8 1.9 3.2 3.6 4.5 4.5 4.6 6.2 6.5 7.7 7.9 9.9 10.2 10.3 10.9 11.1 11.1 11.6 11.8 12.0 13.1 13.5 13.7 14.1 14.2 14.7 15.0 15.1 15.5 15.8 16.0 17.5 18.2 20.2 21.1 21.5 22.2 22.4 23.1 24.5 25.7 28.5 34.6 38.5 43.0 55.6 71.3 77.8 A. Measures of Central Tendency We are to calculate: Mean, Median, Mode The data (already ordered) is: 0.8, 1.4, 1.8, 1.9, 3.2, 3.6, 4.5, 4.5, 4.6, 6.2, 6.5, 7.7, 7.9, 9.9, 10.2, 10.3, 10.9, 11.1, 11.1, 11.6, 11.8, 12.0, 13.1, 13.5, 13.7, 14.1, 14.2, 14.7, 15.0, 15.1, 15.5,…arrow_forwardPEER REPLY 1: Choose a classmate's Main Post. 1. Indicate a range of values for the independent variable (x) that is reasonable based on the data provided. 2. Explain what the predicted range of dependent values should be based on the range of independent values.arrow_forwardIn a company with 80 employees, 60 earn $10.00 per hour and 20 earn $13.00 per hour. Is this average hourly wage considered representative?arrow_forward
 Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt

