Discrete Mathematics With Applications
5th Edition
ISBN: 9781337694193
Author: EPP, Susanna S.
Publisher: Cengage Learning,
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 12.2, Problem 9ES
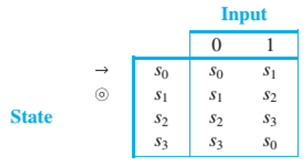
In 8 and 9, a finite-state automaton is given by an annotated next-state table. For each automaton:
a. Find its states.
b. Find its input symbols.
c. Find its initial state.
d. Find its accepting states.
e. Draw its transition diagram.
9. Next-State Table
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Human genetic material (DNA) is made up of sequences of the molecules adenosine (A), guanine (G), cytosine (C), and thymine (T), which are called bases. A codon is a sequence of three bases. Replicates are allowed, so AAA, CGC, and so forth are codons. Codons are important because each codon causes a different amino acid to be included in a protein.
a. How many different codons are there?
b. How many different codons are there in which all three bases are different?
c. The bases A and G are called purines, while C and T are called pyrimidines. How many different codons are there in which the third base is a purine and the others are pyrimidines?
d. What is the probability that all three bases are different?
e. What is the probability that the third base is a purine and the others are pyrimidines?
A DNA molecule is shown below. A nucleotide is represented by one of the letters {a, t, c, g}. A codon is defined to be a triplet of nucleotides. The order of the nucleotides in a codon is significant, and the nucleotides can be
repeated. These codons are important in determining how DNA is transformed into protein. How many different codons are possible?
codons
S = sugar
p = phosphate
g = guanine
C = cytosine
a = adenine
t = thymine
bases
Describe the possible inputs of S(n) using words.
Chapter 12 Solutions
Discrete Mathematics With Applications
Ch. 12.1 - If x and y are strings, the concatenation of x and...Ch. 12.1 - Prob. 2TYCh. 12.1 - Prob. 3TYCh. 12.1 - Prob. 4TYCh. 12.1 - Prob. 5TYCh. 12.1 - Prob. 6TYCh. 12.1 - Prob. 7TYCh. 12.1 - Use of a single dot in a regular expression stands...Ch. 12.1 - Prob. 9TYCh. 12.1 - If r is a regular expression, the notation r +...
Ch. 12.1 - Prob. 11TYCh. 12.1 - Prob. 12TYCh. 12.1 - Prob. 1ESCh. 12.1 - Prob. 2ESCh. 12.1 - Prob. 3ESCh. 12.1 - In 4—6, describe L1L2,L1L2, and (L1L2)*for the...Ch. 12.1 - Prob. 5ESCh. 12.1 - Prob. 6ESCh. 12.1 - Prob. 7ESCh. 12.1 - Prob. 8ESCh. 12.1 - In 7—9, add parentheses to emphasize the order of...Ch. 12.1 - Prob. 10ESCh. 12.1 - In 10—12, use the rules about order of precedence...Ch. 12.1 - Prob. 12ESCh. 12.1 - In 13—15, use set notation to derive the language...Ch. 12.1 - Prob. 14ESCh. 12.1 - Prob. 15ESCh. 12.1 - Prob. 16ESCh. 12.1 - In 16—18, write five strings that belong to the...Ch. 12.1 - Prob. 18ESCh. 12.1 - Prob. 19ESCh. 12.1 - Prob. 20ESCh. 12.1 - In 19—21, use words to describe the language...Ch. 12.1 - Prob. 22ESCh. 12.1 - In 22—24, indicate whether the given strings...Ch. 12.1 - Prob. 24ESCh. 12.1 - Prob. 25ESCh. 12.1 - Prob. 26ESCh. 12.1 - In 25—27, find a regular expression that defines...Ch. 12.1 - Let r, s, and t be regular expressions over...Ch. 12.1 - Prob. 29ESCh. 12.1 - Prob. 30ESCh. 12.1 - Prob. 31ESCh. 12.1 - In 31—39, write a regular expression to define the...Ch. 12.1 - Prob. 33ESCh. 12.1 - Prob. 34ESCh. 12.1 - Prob. 35ESCh. 12.1 - Prob. 36ESCh. 12.1 - Prob. 37ESCh. 12.1 - Prob. 38ESCh. 12.1 - Prob. 39ESCh. 12.1 - Prob. 40ESCh. 12.1 - Write a regular expression to define the set of...Ch. 12.2 - The five objects that make up a finite-state...Ch. 12.2 - The next-state table for an automaton shows the...Ch. 12.2 - In the annotated next-state table, the initial...Ch. 12.2 - A string w consisting of input symbols is accepted...Ch. 12.2 - The language accepted by a finite-state automaton...Ch. 12.2 - If N is the next-stale function for a finite-state...Ch. 12.2 - One part of Kleene’s theorem says that given any...Ch. 12.2 - The second part of Kleene’s theorem says that...Ch. 12.2 - A regular language is .__________Ch. 12.2 - Given the language consisting of all strings of...Ch. 12.2 - Find the state of the vending machine in Example...Ch. 12.2 - Prob. 2ESCh. 12.2 - Prob. 3ESCh. 12.2 - Prob. 4ESCh. 12.2 - Prob. 5ESCh. 12.2 - In 2—7, a finite-state automaton is given by a...Ch. 12.2 - In 2—7, a finite-state automaton is given by a...Ch. 12.2 - In 8 and 9, a finite-state automaton is given by...Ch. 12.2 - In 8 and 9, a finite-state automaton is given by...Ch. 12.2 - A finite-state automaton A given by the transition...Ch. 12.2 - A finite-state automaton A given by the transition...Ch. 12.2 - Prob. 12ESCh. 12.2 - Consider again the finite-state automaton of...Ch. 12.2 - In each of 14—19, (a) find the language accepted...Ch. 12.2 - Prob. 15ESCh. 12.2 - Prob. 16ESCh. 12.2 - Prob. 17ESCh. 12.2 - Prob. 18ESCh. 12.2 - Prob. 19ESCh. 12.2 - In each of 20—28, (a) design an automaton with the...Ch. 12.2 - Prob. 21ESCh. 12.2 - Prob. 22ESCh. 12.2 - Prob. 23ESCh. 12.2 - Prob. 24ESCh. 12.2 - Prob. 25ESCh. 12.2 - Prob. 26ESCh. 12.2 - In each of 20—28, (a) design an automaton with the...Ch. 12.2 - Prob. 28ESCh. 12.2 - Prob. 29ESCh. 12.2 - Prob. 30ESCh. 12.2 - In 29—47, design a finite-state automaton to...Ch. 12.2 - Prob. 32ESCh. 12.2 - Prob. 33ESCh. 12.2 - Prob. 34ESCh. 12.2 - In 29—47, design a finite-state automaton to...Ch. 12.2 - Prob. 36ESCh. 12.2 - Prob. 37ESCh. 12.2 - Prob. 38ESCh. 12.2 - Prob. 39ESCh. 12.2 - Prob. 40ESCh. 12.2 - Prob. 41ESCh. 12.2 - Prob. 42ESCh. 12.2 - Prob. 43ESCh. 12.2 - Prob. 44ESCh. 12.2 - Prob. 45ESCh. 12.2 - In 29—47, design a finite-state automaton to...Ch. 12.2 - Prob. 47ESCh. 12.2 - Prob. 48ESCh. 12.2 - Write a computer algorithm that simulates the...Ch. 12.2 - Prob. 50ESCh. 12.2 - Prob. 51ESCh. 12.2 - Prob. 52ESCh. 12.2 - Prob. 53ESCh. 12.2 - a. Let A be a finite-state automaton with input...Ch. 12.3 - Given a finite-state automaton A with...Ch. 12.3 - Prob. 2TYCh. 12.3 - Given states s and t in a finite-state automaton...Ch. 12.3 - Prob. 4TYCh. 12.3 - Prob. 5TYCh. 12.3 - Consider the finite-state automaton A given by the...Ch. 12.3 - Consider the finite-state automaton A given by the...Ch. 12.3 - Consider the finite-state automaon A discussed in...Ch. 12.3 - Consider the finite-state automaton given by the...Ch. 12.3 - Consider the finite-state automaton given by the...Ch. 12.3 - Consider the finite-state automaton given by the...Ch. 12.3 - Prob. 7ESCh. 12.3 - Prob. 8ESCh. 12.3 - Prob. 9ESCh. 12.3 - Prob. 10ESCh. 12.3 - Prob. 11ESCh. 12.3 - Prob. 12ESCh. 12.3 - Prob. 13ESCh. 12.3 - Prob. 14ESCh. 12.3 - Prob. 15ESCh. 12.3 - Prob. 16ESCh. 12.3 - Prob. 17ESCh. 12.3 - Prob. 18ES
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Six students are taking a taking a programming class. There are a total of eleven programming projects, and students are required to work on these projects in groups of three. By the end of each project, each group is unhappy, and the students never want to work in that particular group of three again (but they are willing to work with individual students they've worked with before). Is it possible for everyone to finish the class without working in the same group twice? If it is possible, provide a schedule; if it is impossible, give a proof.arrow_forwardTwelve luxury cars (4 VW, 4 BMW and 4 Mercedes Benz) are booked by their owners for service at a workshop in Randburg. Suppose the mechanic services one car at any given time. In how many different ways may the cars be serviced in such a way that every BMW car is immediately preceded by a VW car?arrow_forwardThe history of 100 workers who lost their employment due to technological advances is reviewed. Each worker was given an alternative job in the same company, found a job with another company in the same field, found a job in a new field, or has been unemployed for 1 year. In addition the union status of each worker is recorded. Complete (a) and (b). Union Nonunion Same Company New Company 38 18 15 7 New Field 6. 8 Unemployed 3 (a) If the selected worker found a job with a new company in the same field, what is the probability that the worker is a union member? (Round to three decimal places as needed.) Enter your answer in the answer box and then click Check Answer.arrow_forward
- Suppose that we have a shipment of 50 microprocessors of which four are defective. In how many ways can we select a set of four microprocessors containing at least two defective microprocessors?arrow_forwardA starting lineup in basketball consists of two guards, two forwards, and a center. (a) A certain college team has on its roster four centers, five guards, five forwards, and one individual (X) who can play either guard or forward. How many different starting lineups can be created? [Hint: Consider lineups without X, then lineups with X as guard, then lineups with X as forward.] 700 X lineups (b) Now suppose the roster has 5 guards, 5 forwards, 3 centers, and 2 "swing players" (X and Y) who can play either guard or forward. If 5 of the 15 players are randomly selected, what is the probability that they constitute a legitimate starting lineup? (Round your answer to three decimal places.) Need Help? Read Itarrow_forwardThe Human Resources office in a company observes the pattern of absences of employees by days of the week. The company is closed on weekends.The company has 100 employees and over 10 weeks (5000 employee appearances) they notice that there were 100 absences, of which 40 were on the days closest to a weekend (Mondays and Fridays.)Let A = an employee is absent on a day which is a Monday or FridayLet B = an employee is absent on a day which is a Tuesday, Wednesday or Thursday.Let C = a day is a Monday or FridayWhat is the event A U B? What is P(A U B) ? Why is A ∩ B = ∅ ? What is P(A) ? What is P(C) ? What is P(A | C)? Are A and C independent?.arrow_forward
- Suppose we have information about the supermarket purchases of 100 million people. Each person goes to the supermarket 100 times in a year and buys 10 of the 1000 items that the supermarket sells. We believe that a pair of terrorists will buy exactly the same set of 10 items (perhaps the ingredients for a bomb?) at some time during the year. If we search for pairs of people who have bought the same set of items, would we expect that any such people found were truly terrorists? plz provide max possible explanatoon.arrow_forwardAn L-M flip-flop works as follows:If LM = 00, the next state of the flip-flop is 1.If LM = 01, the next state of the flip-flop is the same as the present state.If LM = 10, the next state of the flip-flop is the complement of the present state.If LM = 11, the next state of the flip-flop is 0.(a) Complete the following table (use don’t-cares when possible): (b) Using this table and Karnaugh maps, derive and minimize the input equationsfor a counter composed of three L-M flip-flops which counts in the followingsequence: ABC = 000, 100, 101, 111, 011, 001, 000, . . .arrow_forwardIn how many ways can a television director sched-ule a sponsor’s six different commercials during the six time slots allocated to commercials during a two-hourprogram?arrow_forward
- Find all centralisers and conjugacy classes in .S3arrow_forward15) The figure below shows a binary symmetric channel where each symbol ("0" or "1") sent is inverted with probability "p", independently of all other symbols. In simple terms, when "0" is transmitted, probability of receiving "1" is "p" and probability of receiving "0" is "1-p". When "1" is transmitted, probability of receiving "0" is "p" and probability of receiving "1" is "1-p". The input X to the binary symmetric channel shown in the figure is '1' with probability 0.8 (P(X = 1) = 0.8). The cross-over probability is p = 1/7. If the received symbol is Y 0, what is the conditional probability that X = 1 was transmitted? X = 0 X = 1 O a. 1/5 O b. 2/5 O c. 3/5 O d. 4/5 = Р 1-P P 1-p Y = 0 Y = 1arrow_forwardA starting lineup in basketball consists of two guards, two forwards, and a center. (a) A certain college team has on its roster four centers, five guards, four forwards, and one individual (X) who can play either guard or forward. How many different starting lineups can be created? [Hint: Consider lineups without X, then lineups with X as guard, then lineups with X as forward.] lineups (b) Now suppose the roster has 5 guards, 5 forwards, 4 centers, and 2 "swing players" (X and Y) who can play either guard or forward. If 5 of the 16 players are randomly selected, what is the probability that they constitute a legitimate starting lineup? (Round your answer to three decimal places.)arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Finite State Machine (Finite Automata); Author: Neso Academy;https://www.youtube.com/watch?v=Qa6csfkK7_I;License: Standard YouTube License, CC-BY
Finite State Machine (Prerequisites); Author: Neso Academy;https://www.youtube.com/watch?v=TpIBUeyOuv8;License: Standard YouTube License, CC-BY