
Concept explainers
The race for the 2013 Academy Award for Actress in a Leading Role was extremely tight, featuring several worthy performances (ABC News online, February 22, 2013). The nominees were Jessica Chastain for Zero Dark thirty, Jennifer Lawrence for Silver Linings Playbook, Emmanuelle Riva for Amour, Quvenzhané Wallis for Beasts of the Southern Wild, and Naomi Watts for the Impossible. In a survey, movie fans who had seen each of the movies for which these five actresses had been nominated were asked to select the actress who was most deserving of the 2013 Academy Award for Actress in a Leading Role. The responses follow.
| 18–30 | 31–4 | 45–58 | Over 58 | |
| Jessica Chastain | 51 | 50 | 41 | 42 |
| Jennifer Lawrence | 63 | 55 | 37 | 50 |
| Emmanuelle Riva | 15 | 44 | 56 | 74 |
| Quvenzhané Wallis | 48 | 25 | 22 | 31 |
| Naomi Watts | 36 | 65 | 62 | 33 |
- a. How large was the sample in this survey?
- b. Jennifer Lawrence received the 2013 Academy Award for Actress in a Leading Role for her performance in Silver Linings Playbook. Did the respondents favor Ms. Lawrence? c. at α = .05, conduct a hypothesis test to determine whether people’s attitude toward the actress who was most deserving of the 2013 Academy Award for Actress in a Leading Role is independent of respondent age. What is your Conclusion?
a.
Find the sample size for the given survey.
Answer to Problem 16E
The sample size is 900.
Explanation of Solution
Calculation:
The given observed frequency
| Actress | Age 18-30 | Age 31-44 | Age 45-58 | Age over 58 | Total |
| Jessica Chastain | 51 | 50 | 41 | 42 | 184 |
| Jennifer Lawrence | 63 | 55 | 37 | 50 | 205 |
| Emmanuelle Riva | 15 | 44 | 56 | 74 | 189 |
| Quvenzhane Wallis | 48 | 25 | 22 | 31 | 126 |
| Naomi Watts | 36 | 65 | 62 | 33 | 196 |
| Total | 213 | 239 | 218 | 230 | 900 |
Thus, the sample size is 900.
b.
Explain whether the respondents favor Ms. Lawrence.
Explanation of Solution
Calculation:
Jennifer Lawrence received the 2013 Academy Award for actress in a leading role for “Silver Lining Playbook”.
The sample proportion of movie fan for Jessica Chastain is,
The sample proportion of movie fan for Jennifer Lawrence is,
The sample proportion of movie fan for Emmanuelle Riva is,
The sample proportion of movie fan for Quvenzhane Wallis is,
The sample proportion of movie fan for Naomi Watts is,
It is clear that, the sample proportion for Jennifer Lawrence is highest. Thus, the respondents favor Ms. Lawrence. However, Jessica Chastain, Emmanuelle Riva and Naomi Watts were also favored by almost as many of fans.
c.
Perform a hypothesis test to determine whether people’s attitude toward the actress who was most deserving of the 2013 Academy Award for Actress in a Leading Role is independent of respondent age at 5% level of significance and draw conclusion of the study.
Answer to Problem 16E
The data provide sufficient evidence to conclude that people’s attitude toward the actress who was most deserving of the 2013 Academy Award for Actress in a Leading Role is not independent of respondent age.
Explanation of Solution
Calculation:
State the test hypotheses.
Null hypothesis:
That is, people’s attitude toward the actress who was most deserving of the 2013 Academy Award for Actress in a Leading Role is independent of respondent age.
Alternative hypothesis:
That is, people’s attitude toward the actress who was most deserving of the 2013 Academy Award for Actress in a Leading Role is not independent of respondent age.
The row and column total is tabulated below:
| Actress | Age 18-30 | Age 31-44 | Age 45-58 | Age over 58 | Total |
| Jessica Chastain | 51 | 50 | 41 | 42 | 184 |
| Jennifer Lawrence | 63 | 55 | 37 | 50 | 205 |
| Emmanuelle Riva | 15 | 44 | 56 | 74 | 189 |
| Quvenzhane Wallis | 48 | 25 | 22 | 31 | 126 |
| Naomi Watts | 36 | 65 | 62 | 33 | 196 |
| Totals | 213 | 239 | 218 | 230 | 900 |
The formula for expected frequency is given below:
The expected frequency for each category is calculated as follows:
| Actress | Age 18-30 | Age 31-44 | Age 45-58 | Age over 58 |
| Jessica Chastain | ||||
| Jennifer Lawrence | ||||
| Emmanuelle Riva | ||||
| Quvenzhane Wallis | ||||
| Naomi Watts |
The formula for chi-square test statistic is given as,
The value of chi-square test statistic is,
Thus, the chi-square test statistic is 77.74.
Degrees of freedom:
The degrees of freedom are
In the given problem
Therefore,
Level of significance:
The given level of significance is
p-value:
Software procedure:
Step -by-step software procedure to obtain p-value using MINITAB software is as follows:
- Select Graph > Probability distribution plot > view probability
- Select chi-square under distribution and enter 12 in degrees of freedom.
- Choose X-Value and Right Tail for the region of the curve to shade.
- Enter the X-value as 77.74 under shaded area.
- Select OK.
- Output using MINITAB software is given below:
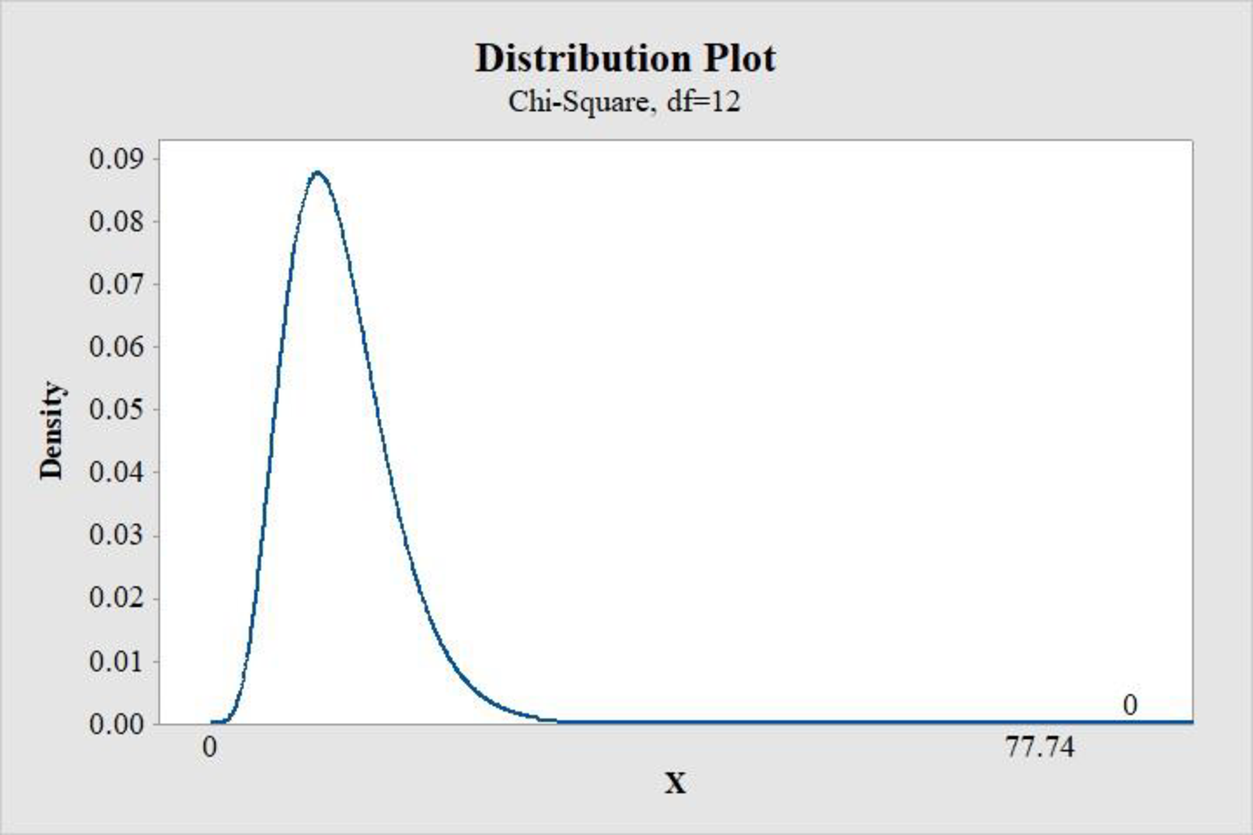
From the MINITAB output, the p-value is 0.
Rejection rule:
If the
Conclusion:
Here, the p-value is less than the level of significance.
That is,
Thus, the decision is “reject the null hypothesis”.
Therefore, the data provide sufficient evidence to conclude that column variable is not independent of row variable. That is, there is an association between column and row variable.
Thus, the data provide sufficient evidence to conclude that people’s attitude toward the actress who was most deserving of the 2013 Academy Award for Actress in a Leading Role is not independent of respondent age.
Want to see more full solutions like this?
Chapter 12 Solutions
Bundle: Statistics for Business & Economics, Loose-Leaf Version, 13th + MindTap Business Statistics with XLSTAT, 1 term (6 months) Printed Access Card
- Businessarrow_forwardWhat is the solution and answer to question?arrow_forwardTo: [Boss's Name] From: Nathaniel D Sain Date: 4/5/2025 Subject: Decision Analysis for Business Scenario Introduction to the Business Scenario Our delivery services business has been experiencing steady growth, leading to an increased demand for faster and more efficient deliveries. To meet this demand, we must decide on the best strategy to expand our fleet. The three possible alternatives under consideration are purchasing new delivery vehicles, leasing vehicles, or partnering with third-party drivers. The decision must account for various external factors, including fuel price fluctuations, demand stability, and competition growth, which we categorize as the states of nature. Each alternative presents unique advantages and challenges, and our goal is to select the most viable option using a structured decision-making approach. Alternatives and States of Nature The three alternatives for fleet expansion were chosen based on their cost implications, operational efficiency, and…arrow_forward
- The following ordered data list shows the data speeds for cell phones used by a telephone company at an airport: A. Calculate the Measures of Central Tendency from the ungrouped data list. B. Group the data in an appropriate frequency table. C. Calculate the Measures of Central Tendency using the table in point B. 0.8 1.4 1.8 1.9 3.2 3.6 4.5 4.5 4.6 6.2 6.5 7.7 7.9 9.9 10.2 10.3 10.9 11.1 11.1 11.6 11.8 12.0 13.1 13.5 13.7 14.1 14.2 14.7 15.0 15.1 15.5 15.8 16.0 17.5 18.2 20.2 21.1 21.5 22.2 22.4 23.1 24.5 25.7 28.5 34.6 38.5 43.0 55.6 71.3 77.8arrow_forwardII Consider the following data matrix X: X1 X2 0.5 0.4 0.2 0.5 0.5 0.5 10.3 10 10.1 10.4 10.1 10.5 What will the resulting clusters be when using the k-Means method with k = 2. In your own words, explain why this result is indeed expected, i.e. why this clustering minimises the ESS map.arrow_forwardwhy the answer is 3 and 10?arrow_forward
- PS 9 Two films are shown on screen A and screen B at a cinema each evening. The numbers of people viewing the films on 12 consecutive evenings are shown in the back-to-back stem-and-leaf diagram. Screen A (12) Screen B (12) 8 037 34 7 6 4 0 534 74 1645678 92 71689 Key: 116|4 represents 61 viewers for A and 64 viewers for B A second stem-and-leaf diagram (with rows of the same width as the previous diagram) is drawn showing the total number of people viewing films at the cinema on each of these 12 evenings. Find the least and greatest possible number of rows that this second diagram could have. TIP On the evening when 30 people viewed films on screen A, there could have been as few as 37 or as many as 79 people viewing films on screen B.arrow_forwardQ.2.4 There are twelve (12) teams participating in a pub quiz. What is the probability of correctly predicting the top three teams at the end of the competition, in the correct order? Give your final answer as a fraction in its simplest form.arrow_forwardThe table below indicates the number of years of experience of a sample of employees who work on a particular production line and the corresponding number of units of a good that each employee produced last month. Years of Experience (x) Number of Goods (y) 11 63 5 57 1 48 4 54 5 45 3 51 Q.1.1 By completing the table below and then applying the relevant formulae, determine the line of best fit for this bivariate data set. Do NOT change the units for the variables. X y X2 xy Ex= Ey= EX2 EXY= Q.1.2 Estimate the number of units of the good that would have been produced last month by an employee with 8 years of experience. Q.1.3 Using your calculator, determine the coefficient of correlation for the data set. Interpret your answer. Q.1.4 Compute the coefficient of determination for the data set. Interpret your answer.arrow_forward
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman





