Chapter 12.1, Problem 63ES

Use a calculator with an e^x key to solve Exercises 57—63. The bar graph shows the percentage of U.S. high school seniors who applied to more than three colleges for selected years from 1980 through 2013.

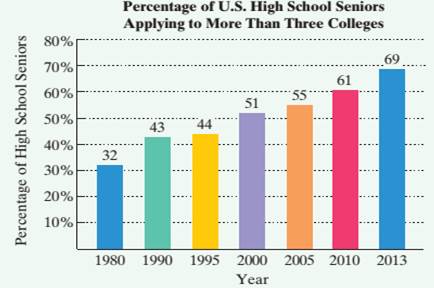
Source: The Higher Education Research Institute

The data in the bar graph at the bottom of the previous page can he modeled by

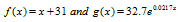
in which f(x) and g(x) represent the percentage of high school seniors who applied to more than three colleges x years after 1980. Use these functions to solve Exercises 57—58. Where necessary, round answers to the nearest percent.

57. a. According to the linear model, what percentage of high school seniors applied to more than three colleges in 2013?

b. According to the exponential model, what percentage of high school seniors applied to more than three colleges in 2013?

c. Which function is a better model for the data shown by the bar graph in 2013?

58. a. According to the linear model, what percentage of high school seniors applied to more than three colleges in 2010?

b. According to the exponential model, what percentage of high school seniors applied to more than three colleges in 2010?

c. Which function is a better model for the data shown by the bar graph in 2010?

59. In college, we study large volumes of information- information that, unfortunately, we do not often retain for very long. The function

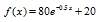
describes the percentage of information, f(x), that a particular person remembers x weeks after learning the information.

a. Substitute 0 for x and, without using a calculator, find the percentage of information remembered at the moment it is first learned.

b. Substitute 1 for x and find the percentage of information that is remembered after 1 week.

c. Find the percentage of information that is remembered after 4 weeks.

d. Find the percentage of information that is remembered after one year (52 weeks).

60. In 1626. Peter Minuit persuaded the Wappinger Indians to sell him Manhattan Island for $24. If the Native Americans had put the $24 into a bank account paying 5% interest, how much would the investment have been worth in the year 2005 if interest were compounded

a. monthly?

b. continuously?

The function

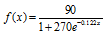
models the percentage, f(x), of people x years old with some

coronary heart disease. Use this function to solve Exercises 61-62. Round answers to the nearest tenth of a percent.

61. Evaluate f(30) and describe what this means in practical terms

62. Evaluate f(70) and describe what this means in practical terms.

63. The function

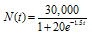
describes the number of people, N(t), who become ill with influenza t weeks after its initial outbreak in a town with 30,000 inhabitants. The horizontal asymptote in the graph indicates that there is a limit to the epidemic's growth.

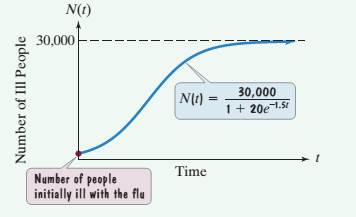
a. How many people became ill with the flu when the epidemic began? (When the epidemic began, t = 0.)

b. How many people were ill by the end of the third week?

c. Why can't the spread of an epidemic simply grow indefinitely? What does the horizontal asymptote shown in the graph indicate about the limiting size of the population that becomes ill?