
Concept explainers
Use a calculator with an ex key to solve Exercises 57—63. The bar graph shows the percentage of U.S. high school seniors who applied to more than three colleges for selected years from 1980 through 2013.
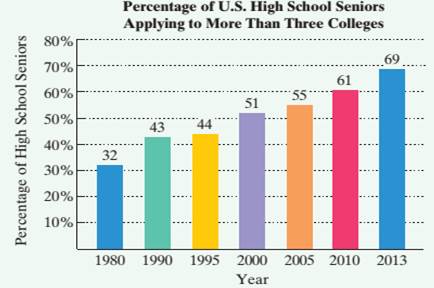
Source: The Higher Education Research Institute
The data in the bar graph at the bottom of the previous page can he modeled by
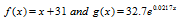
in which f(x) and g(x) represent the percentage of high school seniors who applied to more than three colleges x years after 1980. Use these functions to solve Exercises 57—58. Where necessary, round answers to the nearest percent.
57. a. According to the linear model, what percentage of high school seniors applied to more than three colleges in 2013?
b. According to the exponential model, what percentage of high school seniors applied to more than three colleges in 2013?
c. Which function is a better model for the data shown by the bar graph in 2013?
58. a. According to the linear model, what percentage of high school seniors applied to more than three colleges in 2010?
b. According to the exponential model, what percentage of high school seniors applied to more than three colleges in 2010?
c. Which function is a better model for the data shown by the bar graph in 2010?
59. In college, we study large volumes of information- information that, unfortunately, we do not often retain for very long. The function

describes the percentage of information, f(x), that a particular person remembers x weeks after learning the information.
a. Substitute 0 for x and, without using a calculator, find the percentage of information remembered at the moment it is first learned.
b. Substitute 1 for x and find the percentage of information that is remembered after 1 week.
c. Find the percentage of information that is remembered after 4 weeks.
d. Find the percentage of information that is remembered after one year (52 weeks).
60. In 1626. Peter Minuit persuaded the Wappinger Indians to sell him Manhattan Island for $24. If the Native Americans had put the $24 into a bank account paying 5% interest, how much would the investment have been worth in the year 2005 if interest were compounded
a. monthly?
b. continuously?
The function
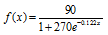
models the percentage, f(x), of people x years old with some
coronary heart disease. Use this function to solve Exercises 61-62. Round answers to the nearest tenth of a percent.
61. Evaluate f(30) and describe what this means in practical terms
62. Evaluate f(70) and describe what this means in practical terms.
63. The function
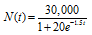
describes the number of people, N(t), who become ill with influenza t weeks after its initial outbreak in a town with 30,000 inhabitants. The horizontal asymptote in the graph indicates that there is a limit to the epidemic's growth.
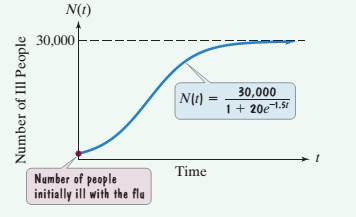
a. How many people became ill with the flu when the epidemic began? (When the epidemic began, t = 0.)
b. How many people were ill by the end of the third week?
c. Why can't the spread of an epidemic simply grow indefinitely? What does the horizontal asymptote shown in the graph indicate about the limiting size of the population that becomes ill?
Want to see the full answer?
Check out a sample textbook solution
Chapter 12 Solutions
Introductory and Intermediate Algebra for College Students, Books a la Carte Edition PLUS MyLab Math (5th Edition)
- Make up two polynomial functions, f(x) and g(x). • f(x) should be of degree 3 or higher. g(x) should be of degree 4 or higher. • Find f(3) in each of the three ways: substitution, remainder theorem (synthetic division), and long division. You should get the same answer three times for f(3). Find g(-2) once using your choice of the three methods.arrow_forwardere are many real-world situations that exhibit exponential and logarithmic nctions. • Describe two real world scenarios, one exponential and one logarithmic. Do not identify yet whether your scenarios are logarithmic or exponential.arrow_forwardstacie is a resident at a medical facility you work at. You are asked to chart the amount of solid food that she consumes.For the noon meal today, she ate 1/2 of a 3 ounce serving of meatloaf, 3/4 of her 3 ounce serving of mashed potatoes, and 1/3 of her 2 ounce serving of green beans. Show in decimal form how many ounces of solid food that Stacie consumedarrow_forward
- I've been struggling with this because of how close the numbers are together!! I would really appreciate if someone could help me❤️arrow_forwardMatrix MЄ R4×4, as specified below, is an orthogonal matrix - thus, it fulfills MTM = I. M (ELES),- m2,1. We know also that all the six unknowns mr,c are non-negative with the exception of Your first task is to find the values of all the six unknowns. Think first, which of the mr,c you should find first. Next, consider a vector v = (-6, 0, 0, 8) T. What's the length of v, i.e., |v|? Using M as transformation matrix, map v onto w by w = Mv provide w with its numeric values. What's the length of w, especially when comparing it to the length of v? Finally, consider another vector p = ( 0, 0, 8, 6) T. What's the angle between v (from above) and p? Using M as transformation matrix, map p onto q by q = Mp - provide q with its numeric values. What's the angle between w and q, especially when comparing it to the angle between v and p?arrow_forward7. (a) (i) Express y=-x²-7x-15 in the form y = −(x+p)²+q. (ii) Hence, sketch the graph of y=-x²-7x-15. (b) (i) Express y = x² - 3x + 4 in the form y = (x − p)²+q. (ii) Hence, sketch the graph of y = x² - 3x + 4. 28 CHAPTER 1arrow_forward
- Part 1 and 2arrow_forwardWhat is the distance between 0,0 and 2,0 aarrow_forwardCompare the interest earned from #1 (where simple interest was used) to #5 (where compound interest was used). The principal, annual interest rate, and time were all the same; the only difference was that for #5, interest was compounded quarterly. Does the difference in interest earned make sense? Select one of the following statements. a. No, because more money should have been earned through simple interest than compound interest. b. Yes, because more money was earned through simple interest. For simple interest you earn interest on interest, not just on the amount of principal. c. No, because more money was earned through simple interest. For simple interest you earn interest on interest, not just on the amount of principal. d. Yes, because more money was earned when compounded quarterly. For compound interest you earn interest on interest, not just on the amount of principal.arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
