
(a)
To find: The P-value to conclude about the ANOVA model.
(a)
Answer to Problem 80E
Solution: The P-value is obtained as 0.000, which indicates that the
Explanation of Solution
Given: The data on the
Store |
Sample size |
Mean |
Sample Standard Deviation |
A |
|||
B |
|||
C |
|||
D |
|||
E |
Calculation: The null and alternative hypothesis of the provided is set as below:
The formulation of ANOVA table will be by the formula provided below:
Sources |
Degree of freedom |
Sum of square |
Mean sum of square |
F |
Groups |
||||
Error |
||||
Total |
Here, N is the total number of samples, I is the number of cases,
By the data provided, the number of groups, total number of groups is:
And,
The degrees of freedom for groups are calculated as:
The degrees of freedom of error are calculated as:
Total degrees of freedom are:
The pooled mean is calculated as:
The sum of squares for groups is calculated as:
The sum of squares of error is calculated:
The Mean Sum of Square of Groups is calculated as:
The Mean Sum of Square of Error is calculated as:
The F-ratio is calculated as:
Now the ANOVA table is:
Sources |
Degree of freedom |
Sum of square |
Mean sum of square |
F- ratio |
Groups |
4 |
11240 |
2810 |
27.93 |
Error |
245 |
24647 |
100.6 |
|
Total |
249 |
The
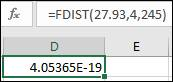
The obtained P-value is approximately 0.000, which is less than the significance level 0.05. So, the null hypothesis is rejected in the provided scenario.
Interpretation: The mean age of the customers at different coffee houses are different.
(b)
To test: The pairwise comparison using LSD method.
(b)
Answer to Problem 80E
Solution: The significant difference between the mean ages of the different coffee houses except the mean age of the store A and store E.
Explanation of Solution
Given: The data on the sample size, mean, and standard deviation of customers of five different stores are provided in the Exercise 12.6, which is shown in the below table.
Store |
Sample size |
Mean |
Sample Standard Deviation |
A |
|||
B |
|||
C |
|||
D |
|||
E |
Calculation: The value of the test statistic for LSD method is obtained through the below mentioned formula:
Where
The required calculation is shown in the below table.
ith Condition |
jth Condition |
Test statistic |
Store A |
Store B |
|
Store C |
||
Store D |
4.985 |
|
Store E |
1.496 |
|
Store B |
Store A |
4.985 |
Store C |
2.991 |
|
Store D |
9.970 |
|
Store E |
6.481 |
|
Store C |
Store A |
1.994 |
Store B |
||
Store C |
6.979 |
|
Store D |
3.490 |
|
Store D |
Store A |
|
Store B |
||
Store C |
||
Store E |
||
Store E |
Store A |
|
Store B |
||
Store C |
||
Store D |
3.490 |
The critical value for the test is obtained from the Table D in the textbook. In the table, there is no value available for 245 degrees of freedom. So, the value corresponding to the 1000 degrees of freedom is considered corresponding to
From the obtained result, it can be determined that a significant difference is present between some of the pairs of means. The only pair of means where the difference is not significant is the means of store A and store E. There is significant difference present between the other pairs of means.
Conclusion: The significant difference between the mean ages of the different coffee houses except the mean age of the store A and store E.
Want to see more full solutions like this?
Chapter 12 Solutions
Introduction to the Practice of Statistics
- A school counselor is conducting a research study to examine whether there is a relationship between the number of times teenagers report vaping per week and their academic performance, measured by GPA. The counselor collects data from a sample of high school students. Write the null and alternative hypotheses for this study. Clearly state your hypotheses in terms of the correlation between vaping frequency and academic performance. EditViewInsertFormatToolsTable 12pt Paragrapharrow_forwardA smallish urn contains 25 small plastic bunnies – 7 of which are pink and 18 of which are white. 10 bunnies are drawn from the urn at random with replacement, and X is the number of pink bunnies that are drawn. (a) P(X = 5) ≈ (b) P(X<6) ≈ The Whoville small urn contains 100 marbles – 60 blue and 40 orange. The Grinch sneaks in one night and grabs a simple random sample (without replacement) of 15 marbles. (a) The probability that the Grinch gets exactly 6 blue marbles is [ Select ] ["≈ 0.054", "≈ 0.043", "≈ 0.061"] . (b) The probability that the Grinch gets at least 7 blue marbles is [ Select ] ["≈ 0.922", "≈ 0.905", "≈ 0.893"] . (c) The probability that the Grinch gets between 8 and 12 blue marbles (inclusive) is [ Select ] ["≈ 0.801", "≈ 0.760", "≈ 0.786"] . The Whoville small urn contains 100 marbles – 60 blue and 40 orange. The Grinch sneaks in one night and grabs a simple random sample (without replacement) of 15 marbles. (a)…arrow_forwardSuppose an experiment was conducted to compare the mileage(km) per litre obtained by competing brands of petrol I,II,III. Three new Mazda, three new Toyota and three new Nissan cars were available for experimentation. During the experiment the cars would operate under same conditions in order to eliminate the effect of external variables on the distance travelled per litre on the assigned brand of petrol. The data is given as below: Brands of Petrol Mazda Toyota Nissan I 10.6 12.0 11.0 II 9.0 15.0 12.0 III 12.0 17.4 13.0 (a) Test at the 5% level of significance whether there are signi cant differences among the brands of fuels and also among the cars. [10] (b) Compute the standard error for comparing any two fuel brands means. Hence compare, at the 5% level of significance, each of fuel brands II, and III with the standard fuel brand I. [10] �arrow_forward
- Analyze the residuals of a linear regression model and select the best response. yes, the residual plot does not show a curve no, the residual plot shows a curve yes, the residual plot shows a curve no, the residual plot does not show a curve I answered, "No, the residual plot shows a curve." (and this was incorrect). I am not sure why I keep getting these wrong when the answer seems obvious. Please help me understand what the yes and no references in the answer.arrow_forwarda. Find the value of A.b. Find pX(x) and py(y).c. Find pX|y(x|y) and py|X(y|x)d. Are x and y independent? Why or why not?arrow_forwardAnalyze the residuals of a linear regression model and select the best response.Criteria is simple evaluation of possible indications of an exponential model vs. linear model) no, the residual plot does not show a curve yes, the residual plot does not show a curve yes, the residual plot shows a curve no, the residual plot shows a curve I selected: yes, the residual plot shows a curve and it is INCORRECT. Can u help me understand why?arrow_forward
- You have been hired as an intern to run analyses on the data and report the results back to Sarah; the five questions that Sarah needs you to address are given below. please do it step by step on excel Does there appear to be a positive or negative relationship between price and screen size? Use a scatter plot to examine the relationship. Determine and interpret the correlation coefficient between the two variables. In your interpretation, discuss the direction of the relationship (positive, negative, or zero relationship). Also discuss the strength of the relationship. Estimate the relationship between screen size and price using a simple linear regression model and interpret the estimated coefficients. (In your interpretation, tell the dollar amount by which price will change for each unit of increase in screen size). Include the manufacturer dummy variable (Samsung=1, 0 otherwise) and estimate the relationship between screen size, price and manufacturer dummy as a multiple…arrow_forwardHere is data with as the response variable. x y54.4 19.124.9 99.334.5 9.476.6 0.359.4 4.554.4 0.139.2 56.354 15.773.8 9-156.1 319.2Make a scatter plot of this data. Which point is an outlier? Enter as an ordered pair, e.g., (x,y). (x,y)= Find the regression equation for the data set without the outlier. Enter the equation of the form mx+b rounded to three decimal places. y_wo= Find the regression equation for the data set with the outlier. Enter the equation of the form mx+b rounded to three decimal places. y_w=arrow_forwardYou have been hired as an intern to run analyses on the data and report the results back to Sarah; the five questions that Sarah needs you to address are given below. please do it step by step Does there appear to be a positive or negative relationship between price and screen size? Use a scatter plot to examine the relationship. Determine and interpret the correlation coefficient between the two variables. In your interpretation, discuss the direction of the relationship (positive, negative, or zero relationship). Also discuss the strength of the relationship. Estimate the relationship between screen size and price using a simple linear regression model and interpret the estimated coefficients. (In your interpretation, tell the dollar amount by which price will change for each unit of increase in screen size). Include the manufacturer dummy variable (Samsung=1, 0 otherwise) and estimate the relationship between screen size, price and manufacturer dummy as a multiple linear…arrow_forward
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman





