
Exercises 49 and 50 refer to the Menger sponge, a three-dimensional cousin of the Sierpinski gasket. The Menger sponge is defined by the following recursive construction rule.
Menger Sponge
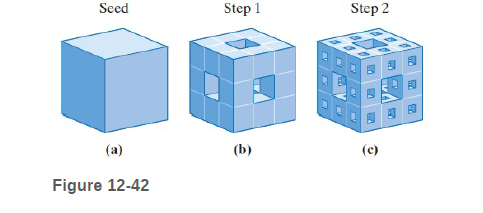
• Start. Start with a solid seed cube [Fig. 12-42(a)].
• Step 1. Subdivide the seed cube into 27 equal subcubes and remove the central cube and the six cubes in the centers of each face. This leaves a "sponge" consisting of 20 solid subcubes, as shown in Fig. 12-42(b)0.
• Step 2. Subdivide each solid subcube into 27 subcubes and remove the central cube and the six cubes in the centers of each face. This gives the "sponge" shown in Fig. 12-42(c). (Call the procedure of removing the central cube and the cubes in the center of each face procedure MS.)
• Steps 3, 4, etc. Apply procedure MS to each cube of the "sponge" obtained in the previous step.
Let H denote the total number of cubic holes obtained at a particular step of the construction of the Menger sponge.
a. Complete the entries in the following table.
| H | |
| Start | 0 |
| Step 1 | 7 |
| Step 2 |
|
| Step 3 | |
| Step 4 | |
| Step 5 |
b. Find a formula that gives the value of H for the sponge obtained at step N of the construction (Hint you will need to use the geometric sum formula from chapter 9)
Want to see the full answer?
Check out a sample textbook solution
Chapter 12 Solutions
Excursions In Modern Mathematics, 9th Edition
- 7. Walkabout. Does this graph have an Euler circuit? If so, find one. If not, explain why not.arrow_forwardBelow, let A, B, and C be sets. 1) Prove (AUB) nC = (ANC) U (BNC).arrow_forwardQ1: find the Reliability of component in the system in fig(1) by minimal cut method. Q2: A component A with constant failure rate 1.5 per 1000 h, B per to 2 in 1000h, A and B in parallel, find the Reliability system? [ by exponential distribution]. Q3: Give an example to find the minimal path and estimate the reliability of this block diagram. Q4: By Tie set method find the Reliability of fig (2) FUZarrow_forward
- A sequence X = (xn) is said to be a contractive sequence if there is a constant 0 < C < 1 so that for all n = N. - |Xn+1 − xn| ≤ C|Xn — Xn−1| -arrow_forward1) Suppose continuous random variable X has sample space S = [1, ∞) and a pdf of the form f(x) = Ce-(2-1)/2. What is the expected value of X?arrow_forwardA sequence X = (xn) is said to be a contractive sequence if there is a constant 0 < C < 1 so that for all n = N. - |Xn+1 − xn| ≤ C|Xn — Xn−1| -arrow_forward
- 1) Find the equation of the tangent line to the graph y=xe at the point (1, 1).arrow_forward3) Suppose that f is differentiable on [0, 5], and f'(x) ≤ 3 over this interval. If f(0) = −1, what is the maximum possible value of f(5)?arrow_forward2) Find the general solution to the differential equation d²x dt² 2 dax = dtarrow_forward
- 2) Prove (AB) UC = (AUC)n (BUC).arrow_forward2) Find the maximum value of f(x, y) = x - y on the circle x² + y² - 4x - 2y - 4 = 0.arrow_forwardBlue Ridge Hot Tubs manufactures and sells two models of hot tubs: the Aqua-Spa and the Hydro-Lux. Howie Jones, the owner and manager of the company, needs to decide how many of each type of hot tub to produce during his next production cycle. Howie buys prefabricated fiberglass hot tub shells from a local supplier and adds the pump and tubing to the shells to create his hot tubs. (This supplier has the capacity to deliver as many hot tub shells as Howie needs.) Howie installs the same type of pump into both hot tubs. He will have only 200 pumps available during his next production cycle. From a manufacturing standpoint, the main difference between the two models of hot tubs is the amount of tubing and labor required. Each Aqua-Spa requires 9 hours of labor and 12 feet of tubing. Each Hydro-Lux requires 6 hours of labor and 16 feet of tubing. Howie expects to have 1,566 production labor hours and 2,880 feet of tubing available during the next production cycle. Howie earns a profit of…arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
