Excursions In Modern Mathematics, 9th Edition
9th Edition
ISBN: 9780134494142
Author: Tannenbaum
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
thumb_up100%
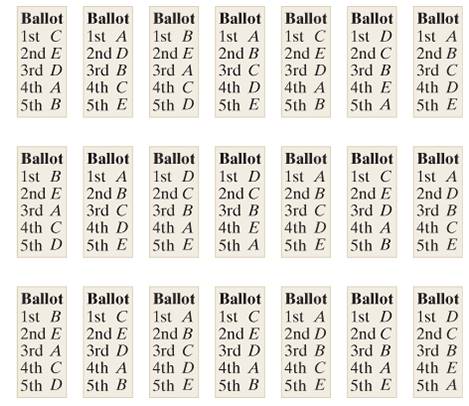
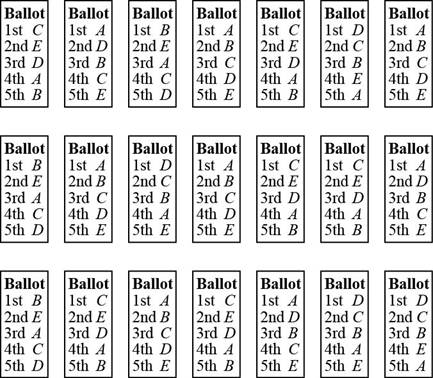
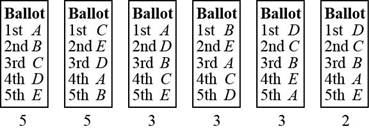
Chapter 1, Problem 1E
Figure 1-8 shows the preference ballots for an election with 21 voters and 5 candidates. Write out the preference schedule for this election.
Figure 1-8
Expert Solution & Answer
To determine
To find:
The preference schedule for the election with given preference ballots.
Answer to Problem 1E
Solution:
The preference schedule for the preference ballots for 21 voters and 5 candidates is,
| Number of Voters | 5 | 5 | 3 | 3 | 3 | 2 |
| 1st Choice | A | C | A | B | D | D |
| 2nd Choice | B | E | D | E | C | C |
| 3rd Choice | C | D | B | A | B | B |
| 4th Choice | D | A | C | C | E | A |
| 5th Choice | E | B | E | D | A | E |
Explanation of Solution
Given:
The preference ballots for 21 voters and 5 candidates are given as,
Calculation:
The ballots of the same preferences are grouped together as,
The preference schedule table for the above ballots is given by,
| Number of Voters | 5 | 5 | 3 | 3 | 3 | 2 |
| 1st Choice | A | C | A | B | D | D |
| 2nd Choice | B | E | D | E | C | C |
| 3rd Choice | C | D | B | A | B | B |
| 4th Choice | D | A | C | C | E | A |
| 5th Choice | E | B | E | D | A | E |
Conclusion:
The preference schedule for the preference ballots for 21 voters and 5 candidates is,
| Number of Voters | 5 | 5 | 3 | 3 | 3 | 2 |
| 1st Choice | A | C | A | B | D | D |
| 2nd Choice | B | E | D | E | C | C |
| 3rd Choice | C | D | B | A | B | B |
| 4th Choice | D | A | C | C | E | A |
| 5th Choice | E | B | E | D | A | E |
Want to see more full solutions like this?
Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Students have asked these similar questions
Please help me first one graphically and the other in matrix
Please help me with this in matrix please
Please solve the differential geometry problem
No chatgpt pls will upvote.
Chapter 1 Solutions
Excursions In Modern Mathematics, 9th Edition
Ch. 1 - Figure 1-8 shows the preference ballots for an...Ch. 1 - Figure 1-9 shows the preference ballots for an...Ch. 1 - An election is held to choose the Chair of the...Ch. 1 - The student body at Eureka High School is having...Ch. 1 - An election is held using the printed-names format...Ch. 1 - Prob. 6ECh. 1 - Prob. 7ECh. 1 - Table 1-30 shows a conventional preference...Ch. 1 - The Demublican Party is holding its annual...Ch. 1 - The Epicurean Society is holding its annual...
Ch. 1 - Table 1-31 shows the preference schedule for an...Ch. 1 - Table 1-32 shows the preference schedule for an...Ch. 1 - Table 1-33 shows the preference schedule for an...Ch. 1 - Table 1-34 shows the preference schedule for an...Ch. 1 - Table 1-35 shows the preference schedule for an...Ch. 1 - Table1-36 shows the preference schedule for an...Ch. 1 - Table 1-25 see Exercise 3 shows the preference...Ch. 1 - Table 1-26 see Exercise 4 shows the preference...Ch. 1 - Table 1-25 see Exercise 3 shows the preference...Ch. 1 - Table 1-26 see Exercise 4 shows the preference...Ch. 1 - Table 1-31see Exercise 11 shows the preference...Ch. 1 - Table 1-32 see Exercise 12 shows the preference...Ch. 1 - Table 1-33 see Exercise 13 shows the preference...Ch. 1 - Table 1-34 Number of voters 6 6 5 4 3 3 1st A B B...Ch. 1 - Table 1-35 Percent of voters 24 23 19 14 11 9 1st...Ch. 1 - Table 1-36 Percent of voters 25 21 15 12 10 9 8...Ch. 1 - The Heisman Award. Table 1-37 shows the results...Ch. 1 - The 2014 AL Cy Young Award. Table 1-38 shows the...Ch. 1 - An election was held using the conventional Borda...Ch. 1 - Imagine that in the voting for the American League...Ch. 1 - Table 1-31 see Exercise 11 shows the preference...Ch. 1 - Table 1-32 see Exercise 12 shows the preference...Ch. 1 - Table1-33 Number of voters 6 5 4 2 2 2 2 1st C A B...Ch. 1 - Table 1-34 See Exercise 14 shows the preference...Ch. 1 - Table1-39_ shows the preference schedule for an...Ch. 1 - Table1-40_ shows the preference schedule for an...Ch. 1 - Table 1-35 see Exercise 15 shows the preference...Ch. 1 - Table 1-36 see Exercise 16 shows the preference...Ch. 1 - Top-Two Instant-Runoff Voting. Exercises 39 and 40...Ch. 1 - Top-Two Instant-Runoff Voting. Exercises 39 and 40...Ch. 1 - Table 1-31 see Exercise 11 shows the preference...Ch. 1 - Table 1-32 See Exercise 12 shows the preference...Ch. 1 - Table 1-33 see Exercise 13 shows the preference...Ch. 1 - Table 1-34 see Exercise 14 shows the preference...Ch. 1 - Table 1-35 see Exercise 15 shows the preference...Ch. 1 - Table 1-36 see Exercise 16 shows the preference...Ch. 1 - Table 1-39 see Exercise 35 shows the preference...Ch. 1 - Table1-40 see Exercise36 shows the preference...Ch. 1 - An election with five candidates A, B. C, D, and E...Ch. 1 - An election with six candidates A, B, C, D, E, and...Ch. 1 - Use Table 1-41 to illustrate why the Borda count...Ch. 1 - Use Table 1-32 to illustrate why the...Ch. 1 - Use Table 1-42 to illustrate why the plurality...Ch. 1 - Use the Math Club election Example 1.10 to...Ch. 1 - Use Table 1-43 to illustrate why the...Ch. 1 - Explain why the method of pair wise comparisons...Ch. 1 - Prob. 57ECh. 1 - Explain why the plurality method satisfies the...Ch. 1 - Explain why the Borda count method satisfies the...Ch. 1 - Explain why the method of pairwise comparisons...Ch. 1 - Two-candidate elections. Explain why when there...Ch. 1 - Alternative version of the Borda count. The...Ch. 1 - Reverse Borda count. Another commonly used...Ch. 1 - The average ranking. The average ranking of a...Ch. 1 - The 2006 Associated Press college football poll....Ch. 1 - The Pareto criterion. The following fairness...Ch. 1 - The 2003-2004 NBA Rookie of the Year vote. Each...Ch. 1 - Top-two IRV is a variation of the...Ch. 1 - The Coombs method. This method is just like the...Ch. 1 - Bucklin voting. This method was used in the early...Ch. 1 - The 2016 NBA MVP vote. The National Basketball...Ch. 1 - The Condorcet loser criterion. If there is a...Ch. 1 - Consider the following fairness criterion: If a...Ch. 1 - Suppose that the following was proposed as a...Ch. 1 - Consider a modified Borda count where a...
Additional Math Textbook Solutions
Find more solutions based on key concepts
1. How much money is Joe earning when he’s 30?
Pathways To Math Literacy (looseleaf)
Length of a Guy Wire A communications tower is located at the top of a steep hill, as shown. The angle of incli...
Precalculus: Mathematics for Calculus (Standalone Book)
Provide an example of a qualitative variable and an example of a quantitative variable.
Elementary Statistics ( 3rd International Edition ) Isbn:9781260092561
(a) Make a stem-and-leaf plot for these 24 observations on the number of customers who used a down-town CitiBan...
APPLIED STAT.IN BUS.+ECONOMICS
For Problems 23-28, write in simpler form, as in Example 4. logbFG
Finite Mathematics for Business, Economics, Life Sciences and Social Sciences
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Q1. A group of five applicants for a pair of identical jobs consists of three men and two women. The employer is to select two of the five applicants for the jobs. Let S denote the set of all possible outcomes for the employer's selection. Let A denote the subset of outcomes corresponding to the selection of two men and B the subset corresponding to the selection of at least one woman. List the outcomes in A, B, AUB, AN B, and An B. (Denote the different men and women by M₁, M2, M3 and W₁, W2, respectively.)arrow_forwardFor the following function, find the full power series centered at a of convergence. 0 and then give the first 5 nonzero terms of the power series and the open interval = f(2) Σ 8 1(x)--(-1)*(3)* n=0 ₤(x) = + + + ++... The open interval of convergence is: 1 1 3 f(x)= = 28 3x6 +1 (Give your answer in help (intervals) .)arrow_forwardQ3 (8 points) Q3. A survey classified a large number of adults according to whether they were diag- nosed as needing eyeglasses to correct their reading vision and whether they use eyeglasses when reading. The proportions falling into the four resulting categories are given in the following table: Use Eyeglasses for Reading Needs glasses Yes No Yes 0.44 0.14 No 0.02 0.40 If a single adult is selected from the large group, find the probabilities of the events defined below. The adult (a) needs glasses. (b) needs glasses but does not use them. (c) uses glasses whether the glasses are needed or not.arrow_forward
- 4. (i) Let a discrete sample space be given by N = {W1, W2, W3, W4}, and let a probability measure P on be given by P(w1) = 0.2, P(w2) = 0.2, P(w3) = 0.5, P(wa) = 0.1. Consider the random variables X1, X2 → R defined by X₁(w1) = 1, X₁(w2) = 2, X2(w1) = 2, X2 (w2) = 2, Find the joint distribution of X1, X2. (ii) X1(W3) = 1, X₁(w4) = 1, X2(W3) = 1, X2(w4) = 2. [4 Marks] Let Y, Z be random variables on a probability space (, F, P). Let the random vector (Y, Z) take on values in the set [0, 1] x [0,2] and let the joint distribution of Y, Z on [0, 1] x [0,2] be given by 1 dPy,z (y, z) ==(y²z+yz2) dy dz. harks 12 Find the distribution Py of the random variable Y. [8 Marks]arrow_forwardNeed help answering wuestionarrow_forwardFor the following function, find the full power series centered at x = 0 and then give the first 5 nonzero terms of the power series and the open interval of convergence. f(x) = Σ| n=0 9 f(x) = 6 + 4x f(x)− + + + ++··· The open interval of convergence is: ☐ (Give your answer in help (intervals) .)arrow_forward
- marks 11 3 3/4 x 1/4 1. There are 4 balls in an urn, of which 3 balls are white and 1 ball is black. You do the following: draw a ball from the urn at random, note its colour, do not return the ball to the urn; draw a second ball, note its colour, return the ball to the urn; finally draw a third ball and note its colour. (i) Describe the corresponding discrete probability space (Q, F, P). [9 Marks] (ii) Consider the following event, A: Among the first and the third balls, one ball is white, the other is black. Write down A as a subset of the sample space and find its probability, P(A). [2 Marks]arrow_forwardThere are 4 balls in an urn, of which 3 balls are white and 1 ball isblack. You do the following:• draw a ball from the urn at random, note its colour, do not return theball to the urn;• draw a second ball, note its colour, return the ball to the urn;• finally draw a third ball and note its colour.(i) Describe the corresponding discrete probability space(Ω, F, P). [9 Marks](ii) Consider the following event,A: Among the first and the third balls, one ball is white, the other is black.Write down A as a subset of the sample space Ω and find its probability, P(A)arrow_forwardLet (Ω, F, P) be a probability space and let X : Ω → R be a randomvariable whose probability density function is given by f(x) = 12 |x|e−|x| forx ∈ R.(i) Find the characteristic function of the random variable X.[8 Marks](ii) Using the result of (i), calculate the first two moments of therandom variable X, i.e., E(Xn) for n = 1, 2. [6 Marks]Total marks 16 (iii) What is the variance of X?arrow_forward
- Let X be a random variable with the standard normal distribution, i.e.,X has the probability density functionfX(x) = 1/√2π e^-(x^2/2)2 .Consider the random variablesXn = 20(3 + X6) ^1/2n e ^x^2/n+19 , x ∈ R, n ∈ N.Using the dominated convergence theorem, prove that the limit exists and find it limn→∞E(Xn)arrow_forwardLet X be a discrete random variable taking values in {0, 1, 2, . . . }with the probability generating function G(s) = E(sX). Prove thatVar(X) = G′′(1) + G′(1) − [G′(1)]2.[5 Marks](ii) Let X be a random variable taking values in [0,∞) with proba-bility density functionfX(u) = (5/4(1 − u^4, 0 ≤ u ≤ 1,0, otherwise. Let y =x^1/2 find the probability density function of Yarrow_forward14 14 4. The graph shows the printing rate of Printer A. Printer B can print at a rate of 25 pages per minute. How does the printing rate for Printer B compare to the printing rate for Printer A? The printing rate for Printer B is than the rate for Printer A because the rate of 25 pages per minute is than the rate of for Printer A. pages per minute RIJOUT 40 fy Printer Rat Number of Pages 8N WA 10 30 20 Printer A 0 0 246 Time (min) Xarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education
Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON
Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning,
Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education
Discrete Mathematics and Its Applications ( 8th I...
Math
ISBN:9781259676512
Author:Kenneth H Rosen
Publisher:McGraw-Hill Education
Mathematics for Elementary Teachers with Activiti...
Math
ISBN:9780134392790
Author:Beckmann, Sybilla
Publisher:PEARSON
Thinking Mathematically (7th Edition)
Math
ISBN:9780134683713
Author:Robert F. Blitzer
Publisher:PEARSON
Discrete Mathematics With Applications
Math
ISBN:9781337694193
Author:EPP, Susanna S.
Publisher:Cengage Learning,
Pathways To Math Literacy (looseleaf)
Math
ISBN:9781259985607
Author:David Sobecki Professor, Brian A. Mercer
Publisher:McGraw-Hill Education
Mod-01 Lec-01 Discrete probability distributions (Part 1); Author: nptelhrd;https://www.youtube.com/watch?v=6x1pL9Yov1k;License: Standard YouTube License, CC-BY
Discrete Probability Distributions; Author: Learn Something;https://www.youtube.com/watch?v=m9U4UelWLFs;License: Standard YouTube License, CC-BY
Probability Distribution Functions (PMF, PDF, CDF); Author: zedstatistics;https://www.youtube.com/watch?v=YXLVjCKVP7U;License: Standard YouTube License, CC-BY
Discrete Distributions: Binomial, Poisson and Hypergeometric | Statistics for Data Science; Author: Dr. Bharatendra Rai;https://www.youtube.com/watch?v=lHhyy4JMigg;License: Standard Youtube License