
Concept explainers
A uniform beam of mass m is inclined at an angle θ to the horizontal. Its upper end (point P) produces a 90° bend in a very rough rope tied to a wall, and its lower end rests on a rough floor (Fig. P12.35). Let μs represent the coefficient of static friction between beam and floor. Assume μs is less than the cotangent of θ. (a) Find an expression for the maximum mass M that can be suspended from the top before the beam slips. Determine (b) the magnitude of the reaction force at the floor and (c) the magnitude of the force exerted by the beam on the rope at P in terms of m, M, and μs.
Figure P12.35
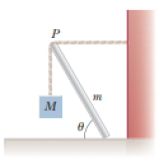
(a)
The expression for the maximum mass that can be suspended from the top surface before the beam starts slip.
Answer to Problem 35AP
The expression for the maximum mass that can be suspended from the top surface before the beam starts slip is
Explanation of Solution
The mass of the beam is
The following figure shows the force diagram of the beam.

Figure-(I)
Formula to calculate the frictional force acting on the base of the beam is,
Here,
Formula to calculate the net torque about the point
Here,
Rearrange the above equation to find
Formula to calculate the net vertical forces is,
Rearrange the above equation to find
Formula to calculate the net horizontal force is,
Substitute
Further simplify the above equation to find
Conclusion:
Therefore, the expression for the maximum mass that can be suspended from the top surface before the beam starts slip is
(b)
The magnitude of the reaction force at the floor.
Answer to Problem 35AP
The magnitude of the reaction force at the floor is
Explanation of Solution
The mass of the beam is
Formula to calculate the net reaction force acting in the floor is,
Here,
Substitute
Conclusion:
Therefore, the magnitude of the reaction force at the floor is
(c)
The magnitude of the force exerted by the beam in the rope at
Answer to Problem 35AP
The magnitude of the force exerted by the beam in the rope at
Explanation of Solution
The mass of the beam is
Since the coefficient of static friction of the floor is less than cotangent of the angle
Substitute
Formula to calculate the magnitude of the net force exerted by the beam in the rope at point
Here,
Substitute
Substitute
Conclusion:
Therefore, the magnitude of the force exerted by the beam in the rope at
Want to see more full solutions like this?
Chapter 12 Solutions
Physics for Scientists and Engineers, Volume 2
- simple diagram to illustrate the setup for each law- coulombs law and biot savart lawarrow_forwardA circular coil with 100 turns and a radius of 0.05 m is placed in a magnetic field that changes at auniform rate from 0.2 T to 0.8 T in 0.1 seconds. The plane of the coil is perpendicular to the field.• Calculate the induced electric field in the coil.• Calculate the current density in the coil given its conductivity σ.arrow_forwardAn L-C circuit has an inductance of 0.410 H and a capacitance of 0.250 nF . During the current oscillations, the maximum current in the inductor is 1.80 A . What is the maximum energy Emax stored in the capacitor at any time during the current oscillations? How many times per second does the capacitor contain the amount of energy found in part A? Please show all steps.arrow_forward
- A long, straight wire carries a current of 10 A along what we’ll define to the be x-axis. A square loopin the x-y plane with side length 0.1 m is placed near the wire such that its closest side is parallel tothe wire and 0.05 m away.• Calculate the magnetic flux through the loop using Ampere’s law.arrow_forwardDescribe the motion of a charged particle entering a uniform magnetic field at an angle to the fieldlines. Include a diagram showing the velocity vector, magnetic field lines, and the path of the particle.arrow_forwardDiscuss the differences between the Biot-Savart law and Coulomb’s law in terms of their applicationsand the physical quantities they describe.arrow_forward
- Explain why Ampere’s law can be used to find the magnetic field inside a solenoid but not outside.arrow_forward3. An Atwood machine consists of two masses, mA and m B, which are connected by an inelastic cord of negligible mass that passes over a pulley. If the pulley has radius RO and moment of inertia I about its axle, determine the acceleration of the masses mA and m B, and compare to the situation where the moment of inertia of the pulley is ignored. Ignore friction at the axle O. Use angular momentum and torque in this solutionarrow_forwardA 0.850-m-long metal bar is pulled to the right at a steady 5.0 m/s perpendicular to a uniform, 0.650-T magnetic field. The bar rides on parallel metal rails connected through a 25-Ω, resistor (Figure 1), so the apparatus makes a complete circuit. Ignore the resistance of the bar and the rails. Please explain how to find the direction of the induced current.arrow_forward
- For each of the actions depicted, determine the direction (right, left, or zero) of the current induced to flow through the resistor in the circuit containing the secondary coil. The coils are wrapped around a plastic core. Immediately after the switch is closed, as shown in the figure, (Figure 1) in which direction does the current flow through the resistor? If the switch is then opened, as shown in the figure, in which direction does the current flow through the resistor? I have the answers to the question, but would like to understand the logic behind the answers. Please show steps.arrow_forwardWhen violet light of wavelength 415 nm falls on a single slit, it creates a central diffraction peak that is 8.60 cm wide on a screen that is 2.80 m away. Part A How wide is the slit? ΟΙ ΑΣΦ ? D= 2.7.10-8 Submit Previous Answers Request Answer × Incorrect; Try Again; 8 attempts remaining marrow_forwardTwo complex values are z1=8 + 8i, z2=15 + 7 i. z1∗ and z2∗ are the complex conjugate values. Any complex value can be expessed in the form of a+bi=reiθ. Find θ for (z1-z∗2)/z1+z2∗. Find r and θ for (z1−z2∗)z1z2∗ Please show all stepsarrow_forward
 Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





