
Concept explainers
Pascal’s Triangle The triangular pattern in the following figure is known as Pascal’s triangle. Pascal's triangle has intrigued mathematician for hundreds of years. Although it is named after the mathematician Blaise Pascal (1623-1662), there is evidence that it was first developed in China in the 1300s. The numbers in Pascal's triangle are created in the following manner. Each row begins and ends with the number 1. Any other number in a row is the sum of the two closest numbers about it. For instance, the first 10 in raw 5 is the sum of the first 4 and the 6 above it in raw 4.
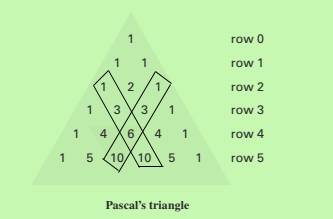
There are many patterns that can be discovered in Pascal's triangle.
a. Find the sum of the numbers in each row, except row 0, of the portion of Pascal's triangle shown above. What pattern do you observe concerning mesa sums? Predict the sum of the numbers in row 9 of Pascal’s triangle.
b. The numbers
Trending nowThis is a popular solution!

Chapter 1 Solutions
EP MATHEMATICAL EXCURSIONS-WEBASSIGN
- Already got wrong chatgpt answer Plz don't use chatgpt answer will upvotearrow_forwardFind all values of x for the given function where the tangent line is horizontal. 3 =√x³-12x² + 45x+5arrow_forwardFind the equation of the tangent line to the graph of the given function at the given value of x. 6 f(x) = x(x² - 4x+5)*; x=2arrow_forward
- 7. Suppose that X is a set, that I is a nonempty set, and that for each i Є I that Yi is a set. Suppose that I is a nonempty set. Prove the following:2 (a) If Y; CX for all i EI, then Uiel Yi C X. ¹See Table 4.8.1 in zyBooks. Recall: Nie X₁ = Vi Є I (x = X₁) and x = Uier X₁ = i Є I (x Є Xi). (b) If XCY; for all i Є I, then X Ciel Yi. (c) U(x)=xnUY. iЄI ΕΙarrow_forwardFind the equation of the tangent line to the graph of the given function at the given value of x. f(x)=√√x+33; x=4arrow_forwardFind g[f(-7)]. f(x) = x² + 1; g(x)=-5x-1arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL


