Find the approximate axial forces, shears, and moments for the all members of the frames using cantilever method.

Question

Want to see more full solutions like this?

Answer 1

Question

Chapter 12, Problem 20P

To determine

Find the approximate axial forces, shears, and moments for the all members of the frames using cantilever method.

Expert Solution & Answer

Explanation of Solution

Given information:

The axial force acting at point I $(HI)$ is 20 kN.

The axial force acting at point E $(HE)$ is 40 kN.

The vertical distance of the member AE, BF, CG, and DH $(L2)$ is 6 m.

The vertical distance of the member EI, FJ, GK, and HL $(L1)$ is 4 m.

The horizontal distance of the members AB, EF, and IJ $(l1)$ is 8 m.

The horizontal distance of the members BC, FG, and JK $(l2)$ is 6 m.

The horizontal distance of the members CD, GH, and KL $(l3)$ is 8 m.

Take the counterclockwise moment is positive and clockwise moment is negative.

The axial force in horizontal direction, towards right is positive and towards left side is negative.

The axial force in vertical direction, towards upward is positive and towards downward is negative.

Calculation:

Insert the internal hinges at the midpoints of all the members of the given frame to obtain the simplified frame for approximate analysis.

Draw the simplified frame as in Figure (1).

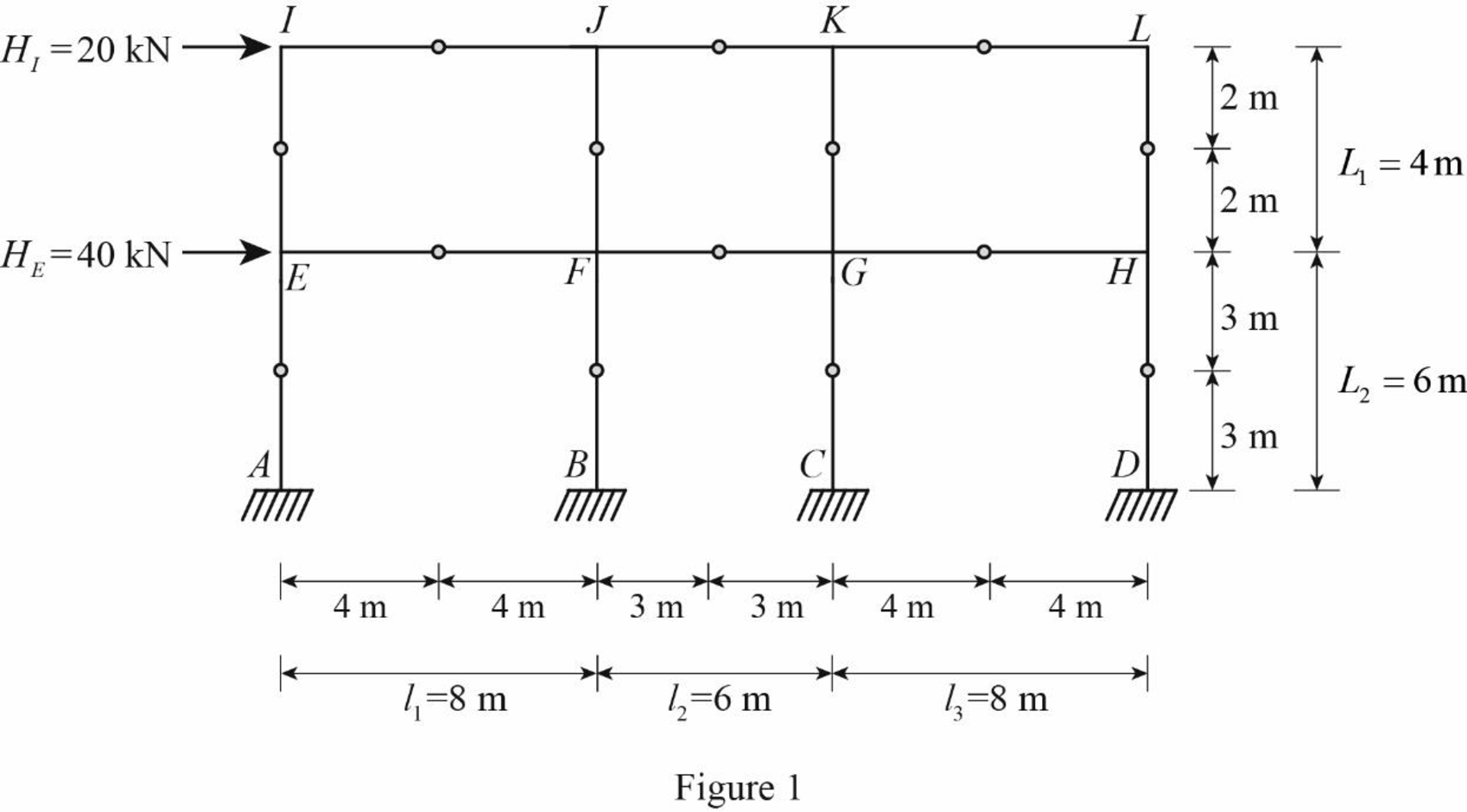
Structural Analysis, Si Edition (mindtap Course List), Chapter 12, Problem 20P , additional homework tip 1

For the calculation of column axial forces of story of the frame, pass an imaginary section aa through the internal hinges at the midheights of columns EI, FJ, GK, and HL, and pass an imaginary section bb through the internal hinges at the midheights of columns AE, BF, CG, and DH.

Draw the free body diagram of the frame portion with the passed imaginary lines as in Figure (2).

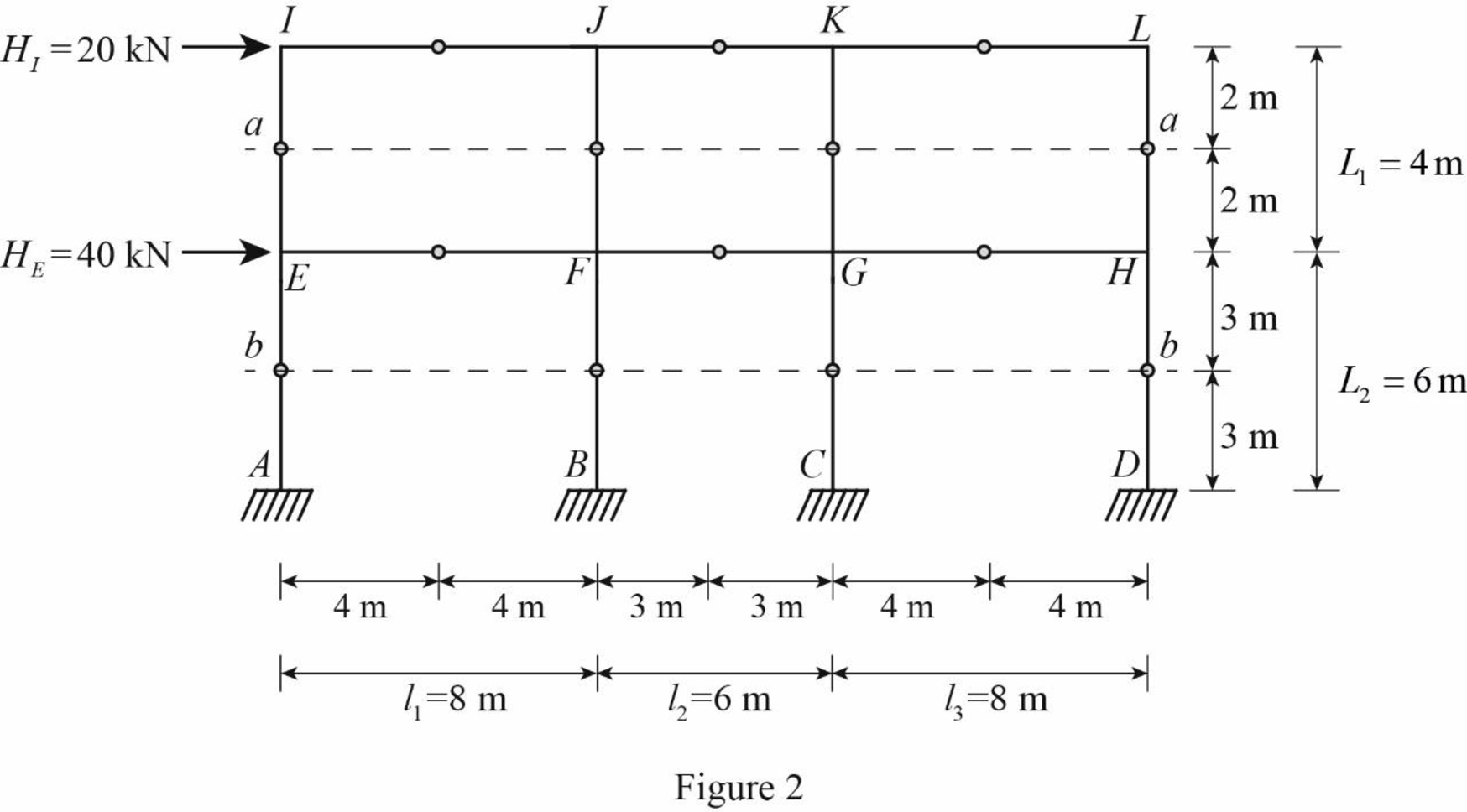
Structural Analysis, Si Edition (mindtap Course List), Chapter 12, Problem 20P , additional homework tip 2

Column axial forces:

Above section aa:

Draw the free body diagram of the frame portion above the section aa as in Figure (3).

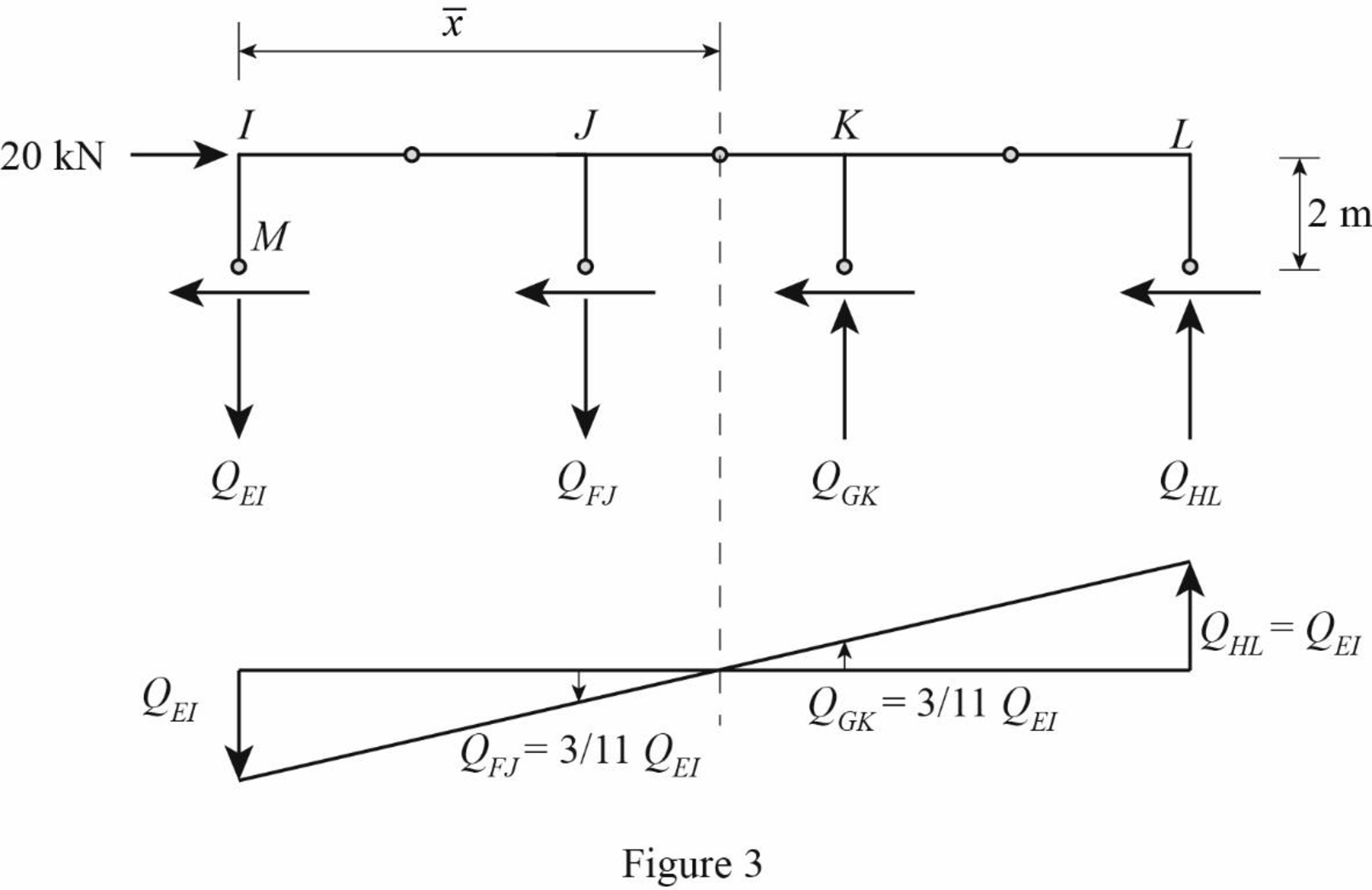
Structural Analysis, Si Edition (mindtap Course List), Chapter 12, Problem 20P , additional homework tip 3

Refer Figure 3.

Determine the location of the centroid using the relation.

$x¯=∑Ax∑A=∑Ax1+Ax2+Ax3+Ax44A$ (1)

Substitute 0 m for $x1$ , 8 m for $x2$ , 14 m for $x3$ , and 22 m for $x4$ in Equation (1).

$x¯=A(0)+A(8)+A(14)+A(22)4A=11 m$

The given lateral load is acting on the frame to the right, therefore the axial force in column EI and FJ located to the left of the centroid, must be tensile, whereas the axial force in column HL and GK placed to the right of the centroid, must be compressive.

Consider the axial forces in the columns are to be linearly proportional to their distances from centroid.

Apply similar triangle rule.

Determine the relationship in column axial force between the member EI and FJ using the relation.

$QFJ=x¯−l1x¯QEI$

Substitute 11 m for $x¯$ and 8 m for $l1$ .

$QFJ=11−811QEI=311QEI$

Determine the relationship in column axial force between the member EI and GK using the relation.

$QGK=(l1+l2)−x¯x¯QEI$

Substitute 8 m for $l1$ , 6 m for $l2$ , and 11 m for $x¯$ .

$QGK=(8+6)−1111QEI=311QEI$

Determine the axial force in the column members EI, FJ, GK, and HL using equilibrium conditions.

Take moment about point M.

$∑MM=0QHL×(l1+l2+l3)+QGK×(l1+l2)−QFJ×l1−HI×L12=0$

Substitute $QEI$ for $QHL$ , 8 m for $l1$ , 6 m for $l2$ , 8 m for $l3$ , $311QEI$ for $QGK$ , $311QEI$ for $QFJ$ , 20 kN for $HI$ , and 4 m for $L1$ .

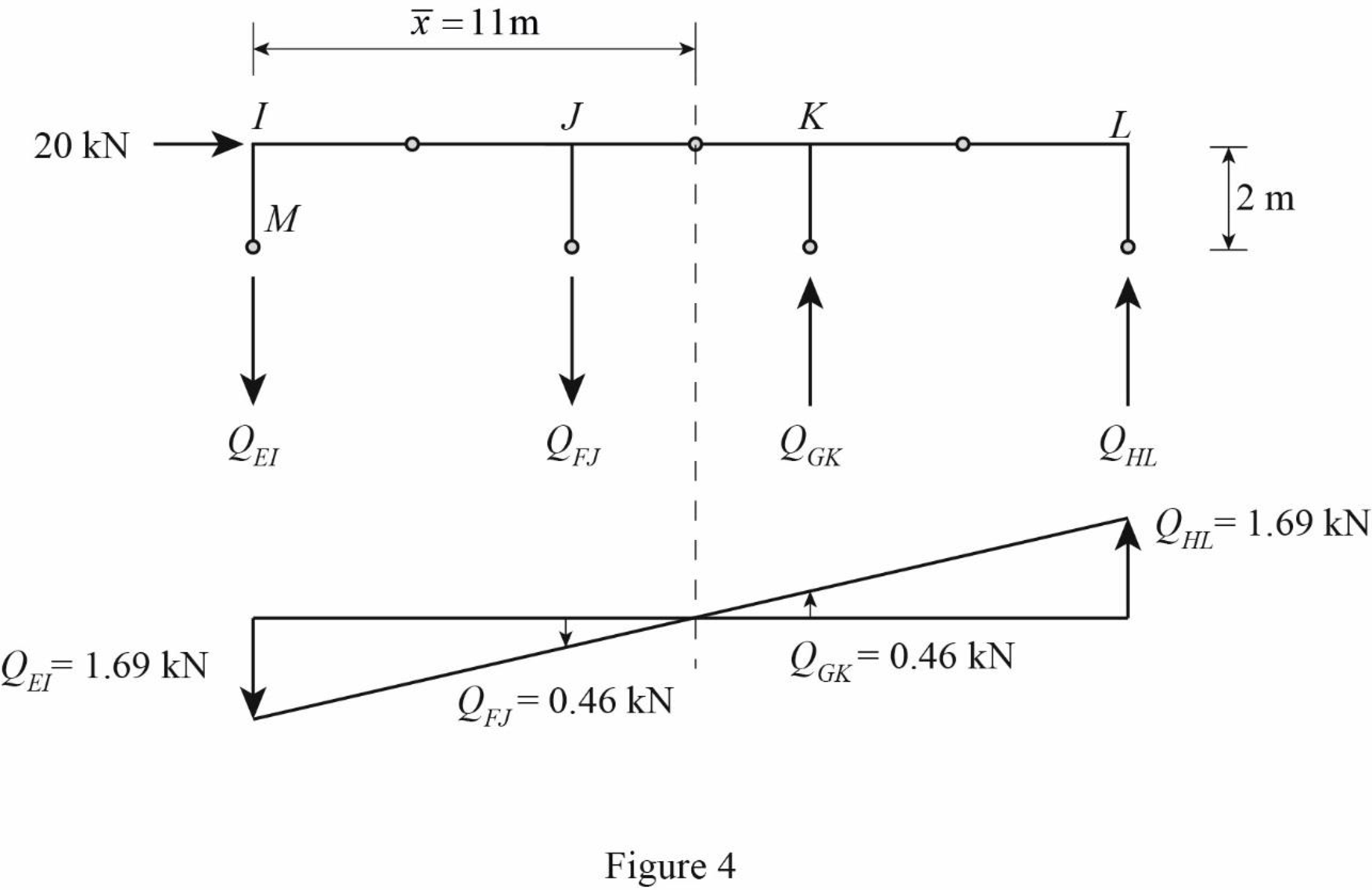
$QEI×(8+6+8)+311QEI×(8+6)−311QEI×8−20×42=0242QEI+42QEI−24QEI=440QEI=440260QEI=1.69 kN$

Determine the axial force in the column members FJ.

$QFJ=311QEI$

Substitute 1.69 kN for $QEI$ .

$QFJ=311×1.69=0.46 kN(↓)$

Determine the axial force in the column members GK.

$QGK=311QEI$

Substitute 1.69 kN for $QEI$ .

$QGK=311×1.69=0.46 kN(↑)$

Determine the axial force in the column members HL.

$QHL=QEI$

Substitute 1.69 kN for $QEI$ .

$QHL=1.69 kN(↑)$

Draw the free body diagram of the frame portion above the section aa with the axial forces in the column members as in Figure (4).

Structural Analysis, Si Edition (mindtap Course List), Chapter 12, Problem 20P , additional homework tip 4

Draw the free body diagram of the frame portion above the section bb as in Figure (5).

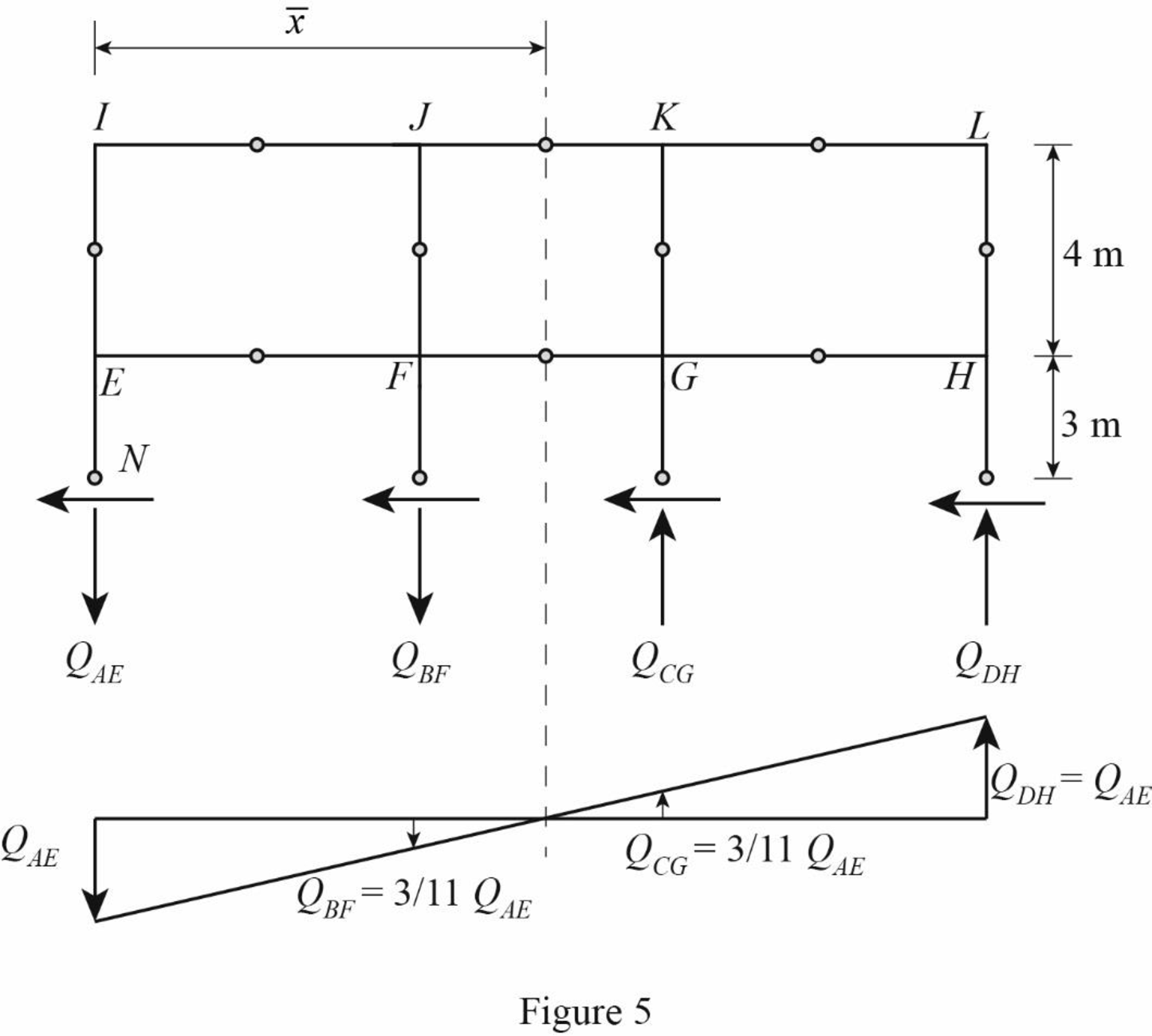
Structural Analysis, Si Edition (mindtap Course List), Chapter 12, Problem 20P , additional homework tip 5

The given lateral load is acting on the frame to the right, therefore the axial force in column AE and BF located to the left of the centroid, must be tensile, whereas the axial force in column CG and DH placed to the right of the centroid, must be compressive.

Determine the relationship in column axial force between the member AE and BF using the relation.

$QBF=x¯−l1x¯QAE$

Substitute 11 m for $x¯$ and 8 m for $l1$ .

$QBF=11−811QAE=311QAE$

Determine the relationship in column axial force between the member AE and CG using the relation.

$QCG=(l1+l2)−x¯x¯QAE$

Substitute 8 m for $l1$ , 6 m for $l2$ , and 11 m for $x¯$ .

$QCG=(8+6)−1111QAE=311QAE$

Determine the axial force in the column members AE, BF, CG, and DH using equilibrium conditions.

Take moment about point N.

$∑MN=0QDH×(l1+l2+l3)+QCG×(l1+l2)−QBF×l1−HI×(L1+L22)−HE×L22=0$

Substitute $QAE$ for $QDH$ , 8 m for $l1$ , 6 m for $l2$ , 8 m for $l3$ , $311QAE$ for $QBF$ , $311QAE$ for $QCG$ , 20 kN for $HI$ , 4 m for $L1$ , 40 kN for $HE$ , and 6 m for $L2$ .

$QAE×(8+6+8)+311QAE×(8+6)−311QAE×8−20×(4+62)−40×62=0242QAE+42QAE−24QAE=2,860QAE=2,860260QAE=11 kN$

Determine the axial force in the column members BF.

$QBF=311QAE$

Substitute 11 kN for $QAE$ .

$QBF=311×11=3 kN(↓)$

Determine the axial force in the column members CG.

$QCG=311QAE$

Substitute 11 kN for $QAE$ .

$QCG=311×11=3 kN(↑)$

Determine the axial force in the column members DH.

$QDH=QAE$

Substitute 11 kN for $QAE$ .

$QDH=11 kN(↑)$

Draw the free body diagram of the frame portion above the section bb with the axial forces in the column members as in Figure (6).

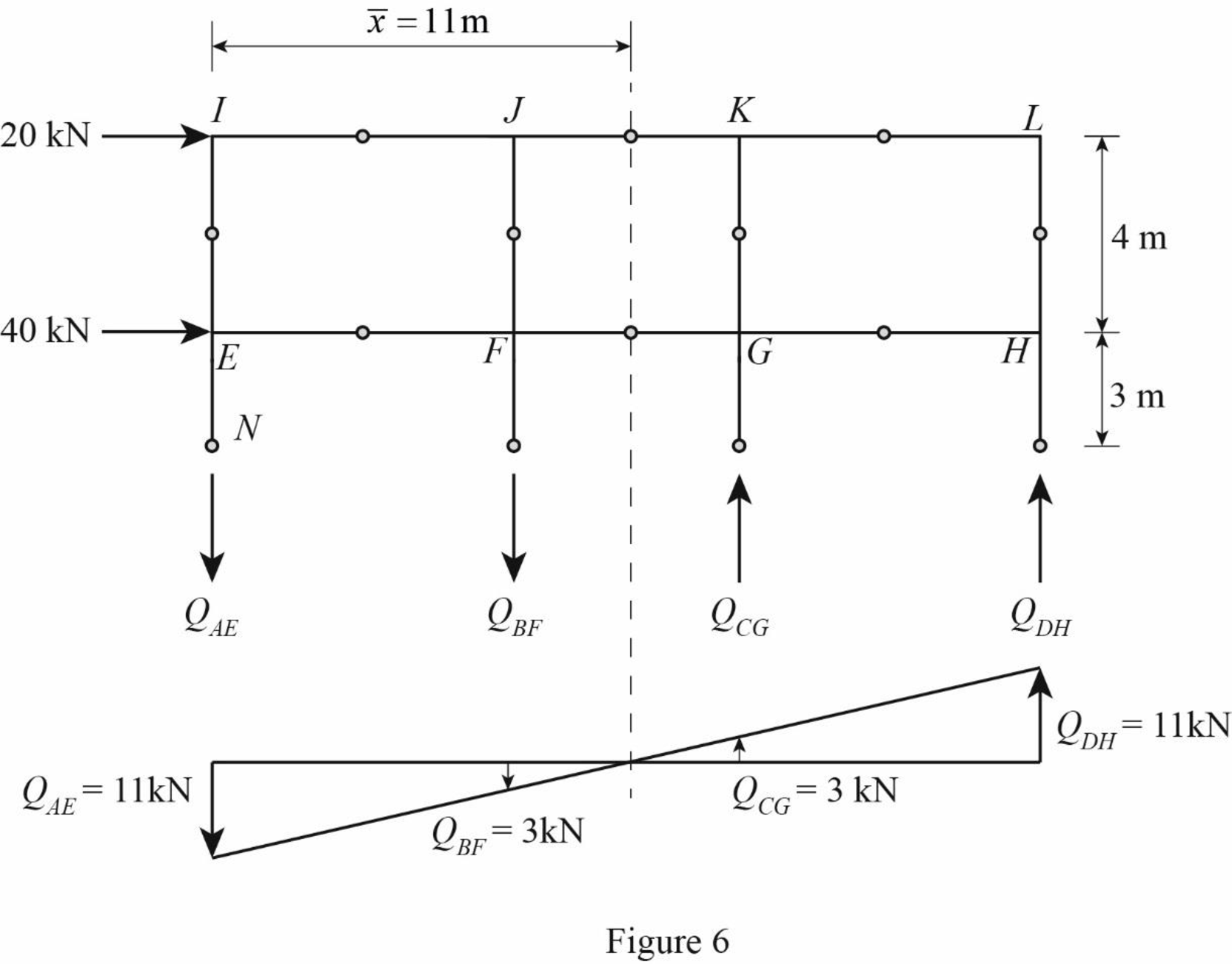
Structural Analysis, Si Edition (mindtap Course List), Chapter 12, Problem 20P , additional homework tip 6

Girder shear and moments:

Consider girder IJ.

Determine the shear at upper left end joint I using equilibrium equation.

$∑FY=0SIJ+QIE=0$

Substitute 1.69 kN for $QIE$ .

$SIJ+1.69 kN=0SIJ=−1.69 kNSIJ=1.69 kN(↓)$

Determine the shear at upper right end joint J using equilibrium equation.

$∑FY=0−SIJ+SJI=0$

Substitute 1.69 kN for $SIJ$ .

$−1.69+SJI=0SJI=1.69 kN(↑)$

Determine the moment at left end of the girder IJ using equilibrium equations.

$MIJ=−SIJ×l12$

Substitute 1.69 kN for $SIJ$ and 8 m for $l1$ .

$MIJ=−1.69×82=6.76 kN⋅m(Clockwise)$

Determine the moment at right end of the girder GH using equilibrium equations.

Take moment about point I.

$∑MG=0−MIJ+SJI×l1+MJI=0$

Substitute $6.76 kN⋅m$ for $MIJ$ , 1.69 kN for $SJI$ , and 8 m for $l1$ .

$−6.76+1.69×8+MJI=0MJI=−6.76 kN⋅mMJI=6.76 kN⋅m(Clockwise)$

Consider girder JK.

Determine the shear at left end joint J using equilibrium equation.

$∑FY=0SJI+SJK+QJF=0$

Substitute 1.69 kN for $SJI$ and 0.46 kN for $QJF$ .

$1.69+SJK+0.46=0SJK=−2.15 kNSJK=2.15 kN(↓)$

Determine the shear at right end joint K using equilibrium equation.

$∑FY=0−SJK+SKJ=0$

Substitute 2.15 kN for $SJK$ .

$−2.15+SJK=0SJK=2.15 kN(↑)$

Determine the moment at left end of the girder JK using equilibrium equations.

$MJK=−SJK×l22$

Substitute 2.15 kN for $SJK$ and 6 m for $l2$ .

$MJK=−2.15×62=−6.45 kN⋅m=6.45 kN⋅m(Clockwise)$

Determine the moment at right end of the girder JK using equilibrium equations.

Take moment about point J.

$∑MJ=0−MJK+SKJ×l2+MKJ=0$

Substitute $6.45 kN⋅m$ for $MJK$ , 2.15 kN for $SKJ$ , and 6 m for $l2$ .

$−6.45+2.15×6+MKJ=0MKJ=−6.45 kN⋅mMKJ=6.45 kN⋅m(Clockwise)$

Consider girder KL.

Determine the shear at left end joint K using equilibrium equation.

$∑FY=0SKJ+SKL−QKG=0$

Substitute 2.15 kN for $SKJ$ and 0.46 kN for $QKG$ .

$2.15+SKL−0.46=0SKL=−1.69 kNSKL=1.69 kN(↓)$

Determine the shear at right end joint L using equilibrium equation.

$∑FY=0−SKL+SLK=0$

Substitute 1.69 kN for $SKL$ .

$−1.69+SKL=0SKL=1.69 kN(↑)$

Determine the moment at left end of the girder KL using equilibrium equations.

$MKL=−SKL×l32$

Substitute 1.69 kN for $SKL$ and 8 m for $l3$ .

$MKL=−1.69×82=−6.76 kN⋅m=6.76 kN⋅m(Clockwise)$

Determine the moment at right end of the girder JK using equilibrium equations.

Take moment about point K.

$∑MK=0−MKL+SLK×l3+MLK=0$

Substitute $6.76 kN⋅m$ for $MJK$ , 1.69 kN for $SLK$ , and 8 m for $l3$ .

$−6.76+1.69×8+MLK=0MLK=−6.76 kN⋅mMLK=6.76 kN⋅m(Clockwise)$

Consider girder EF.

Determine the shear at left end joint E using equilibrium equation.

$∑FY=0SEF−QEI+QEA=0$

Substitute 1.69 kN for $QEI$ and 11 kN for $QEA$ .

$SEF−1.69+11=0SEF=−9.31 kNSEF=9.31 kN(↓)$

Determine the shear at right end joint F using equilibrium equation.

$∑FY=0−SEF+SFE=0$

Substitute 9.31 kN for $SEF$ .

$−9.31+SFE=0SFE=9.31 kN(↑)$

Determine the moment at left end of the girder EF using equilibrium equations.

$MEF=−SEF×l12$

Substitute 9.31 kN for $SEF$ and 8 m for $l1$ .

$MEF=−9.31×82=−37.24 kN⋅m=37.24 kN⋅m(Clockwise)$

Determine the moment at right end of the girder EF using equilibrium equations.

Take moment about point E.

$∑ME=0−MEF+SFE×l1+MFE=0$

Substitute $37.24 kN⋅m$ for $MEF$ , 9.31 kN for $SFE$ , and 8 m for $l1$ .

$−37.24+9.31×8+MFE=0MFE=−37.24 kN⋅mMFE=37.24 kN⋅m(Clockwise)$

Consider girder FG.

Determine the shear at left end joint F using equilibrium equation.

$∑FY=0SFE+SFG−QFJ+QFB=0$

Substitute 9.31 kN for $SFE$ , 0.46 kN for $QFJ$ , and 3 kN for $QFB$ .

$9.31+SFG−0.46+3=0SFG=−11.85 kNSFG=11.85 kN(↓)$

Determine the shear at right end joint G using equilibrium equation.

$∑FY=0−SFG+SGF=0$

Substitute 11.85 kN for $SFG$ .

$−11.85+SGF=0SGF=11.85 kN(↑)$

Determine the moment at left end of the girder FG using equilibrium equations.

$MFG=−SFG×l22$

Substitute 11.85 kN for $SFG$ and 6 m for $l2$ .

$MFG=−11.85×62=−35.55 kN⋅m=35.55 kN⋅m(Clockwise)$

Determine the moment at right end of the girder FG using equilibrium equations.

Take moment about point F.

$∑MF=0−MFG+SGF×l2+MGF=0$

Substitute $35.55 kN⋅m$ for $MFG$ , 11.85 kN for $SGF$ , and 6 m for $l2$ .

$−35.55+11.85×6+MGF=0MGF=−35.55 kN⋅mMGF=35.55 kN⋅m(Clockwise)$

Consider girder GH.

Determine the shear at left end joint G using equilibrium equation.

$∑FY=0SGH+SGF+QGK−QGC=0$

Substitute 11.85 kN for $SGF$ , 0.46 kN for $QGK$ , and 3 kN for $QGC$ .

$SGH+11.85+0.46−3=0SGH=−9.31 kNSGH=9.31 kN(↓)$

Determine the shear at right end joint H using equilibrium equation.

$∑FY=0−SGH+SHG=0$

Substitute 9.31 kN for $SGH$ .

$−9.31+SHG=0SHG=9.31 kN(↑)$

Determine the moment at left end of the girder GH using equilibrium equations.

$MGH=−SGH×l32$

Substitute 9.31 kN for $SGH$ and 8 m for $l3$ .

$MGH=−9.31×82=−37.24 kN⋅m=37.24 kN⋅m(Clockwise)$

Determine the moment at right end of the girder GH using equilibrium equations.

Take moment about point G.

$∑MG=0−MGH+SHG×l3+MHG=0$

Substitute $37.24 kN⋅m$ for $MGH$ , 9.31 kN for $SHG$ , and 8 m for $l3$ .

$−37.24+9.31×8+MHG=0MHG=−37.24 kN⋅mMHG=37.24 kN⋅m(Clockwise)$

Column moments and shears:

Column moment for member EI, FJ, GK, and HL:

Determine the moment at the column member EI using moment equilibrium of joints.

Apply the moment equilibrium of joints at I.

$∑M=0MIE−MIJ=0$

Substitute $6.76 kN⋅m$ for $MIJ$ .

$MIE−6.76=0MIE=6.76 kN⋅m(Counterclockwise)$

The moment at the column member EI is $MEI=MIE=6.76 kN⋅m(Counterclockwise)$ .

Determine the moment at the column member FJ.

Apply the moment equilibrium of joints at J.

$∑M=0−MJI−MJK+MJF=0$

Substitute $6.76 kN⋅m$ for $MIJ$ and $6.45 kN⋅m$ for $MJK$ .

$−6.76−6.45+MJF=0MJF=13.21 kN⋅m(Counterclockwise)$

The moment at the column member FJ is $MJF=MFJ=13.21 kN⋅m(Counterclockwise)$ .

Determine the moment at the column member GK.

Apply the moment equilibrium of joints at K.

$∑M=0−MKJ−MKL+MKG=0$

Substitute $6.45 kN⋅m$ for $MKJ$ and $6.76 kN⋅m$ for $MKL$ .

$−6.45−6.76+MKG=0MKG=13.21 kN⋅m(Counterclockwise)$

The moment at the column member GK is $MKG=MGK=13.21 kN⋅m(Counterclockwise)$ .

Determine the moment at the column member HL using moment equilibrium of joints.

Apply the moment equilibrium of joints at L.

$∑M=0−MLK+MLH=0$

Substitute $6.76 kN⋅m$ for $MLK$ .

$−6.76+MLH=0MLH=6.76 kN⋅m(Counterclockwise)$

The moment at the column member HL is $MHL=MLH=60 kN⋅m(Counterclockwise)$ .

Column shear for member EI, FJ, GK, and HL:

Determine the shear at the end I in the column member EI using the relation.

$SIE=MIEL12$

Substitute $6.76 kN⋅m$ for $MIE$ and 4 m for $L1$ .

$SIE=6.7642=3.38 kN(→)$

The shear at the column member EI must act towards right, so that it can produce Clockwise moment to balance the counterclockwise moment at joint I.

Determine the shear at the end of the column E using equilibrium conditions.

$∑FX=0SIE+SEI=0$

Substitute 3.38 kN for $SIE$ .

$3.38+SEI=0SEI=−3.38 kNSEI=3.38 kN(←)$

Determine the shear at the end J in the column member FJ using the relation.

$SJF=MJFL12$

Substitute $13.21 kN⋅m$ for $MEH$ and 4 m for $L1$ .

$SJF=13.2142=6.61 kN(→)$

The shear at the column member JF must act towards right, so that it can produce Clockwise moment to balance the counterclockwise moment at joint J.

Determine the shear at the end of the column F using equilibrium conditions.

$∑FX=0SJF+SFJ=0$

Substitute 6.61 kN for $SJF$ .

$6.61+SFJ=0SFJ=−6.61 kNSFJ=6.61 kN(←)$

Determine the shear at the end K in the column member GK using the relation.

$SKG=MKGL12$

Substitute $13.21 kN⋅m$ for $MKG$ and 4 m for $L1$ .

$SKG=13.2142=6.61 kN(→)$

The shear at the column member KG must act towards right, so that it can produce Clockwise moment to balance the counterclockwise moment at joint K.

Determine the shear at the end of the column G using equilibrium conditions.

$∑FX=0SKG+SGK=0$

Substitute 6.61 kN for $SKG$ .

$6.61+SGK=0SGK=−6.61 kNSGK=6.61 kN(←)$

Determine the shear at the end L in the column member HL using the relation.

$SLH=MLHL12$

Substitute $6.76 kN⋅m$ for $MLH$ and 4 m for $L1$ .

$SLH=6.7642=3.38 kN(→)$

The shear at the column member LH must act towards right, so that it can produce Clockwise moment to balance the counterclockwise moment at joint L.

Determine the shear at the end of the column H using equilibrium conditions.

$∑FX=0SLH+SHL=0$

Substitute 3.38 kN for $SLH$ .

$3.38+SHL=0SHL=−3.38 kNSHL=3.38 kN(←)$

Column moment for member AE, BF, CG, and DH:

Determine the moment at the column member AE using moment equilibrium of joints.

Apply the moment equilibrium of joints at E.

$∑M=0MEA−MEF+MEI=0$

Substitute $37.24 kN⋅m$ for $MEF$ and $6.76 kN⋅m$ for $MEI$ .

$MEA−37.24+6.76=0MEA=30.48 kN⋅m(Counterclockwise)$

The moment at the column member AE is $MAE=MEA=30.48 kN⋅m(Counterclockwise)$ .

Determine the moment at the column member BF.

Apply the moment equilibrium of joints at F.

$∑M=0MFB−MFE−MFG+MFJ=0$

Substitute $37.24 kN⋅m$ for $MFE$ , $35.55 kN⋅m$ for $MFE$ , and $13.21 kN⋅m$ for $MFJ$ .

$MFB−37.24−35.55+13.21=0MFB=59.58 kN⋅m(Counterlockwise)$

The moment at the column member BF is $MFB=MBF=59.58 kN⋅m(Counterlockwise)$ .

Determine the moment at the column member CG using moment equilibrium of joints.

Apply the moment equilibrium of joints at C.

$∑M=0MGC−MGF−MGH+MGK=0$

Substitute $35.55 kN⋅m$ for $MGF$ , $37.24 kN⋅m$ for $MGH$ , and $13.21 kN⋅m$ for $MGK$ .

$MGC−35.55−37.24+13.21=0MGC=59.58 kN⋅m(Counterlockwise)$

The moment at the column member CG is $MCG=MGC=59.58 kN⋅m(Counterlockwise)$ .

Determine the moment at the column member DH using moment equilibrium of joints.

Apply the moment equilibrium of joints at H.

$∑M=0MHD−MHG+MHL=0$

Substitute $37.24 kN⋅m$ for $MHG$ and $6.76 kN⋅m$ for $MHL$ .

$MHD−37.24+6.76=0MHD=30.48 kN⋅m(Counterclockwise)$

The moment at the column member DH is $MDH=MHD=30.48 kN⋅m(Counterclockwise)$ .

Column shear for member AE, BF, CG, and DH:

Determine the shear at the end E in the column member AE using the relation.

$SEA=MEAL22$

Substitute $30.48 kN⋅m$ for $MDA$ and 6 m for $L2$ .

$SEA=30.4862=10.16 kN(→)$

The shear at the column member EA must act towards right, so that it can produce Clockwise moment to balance the counterclockwise moment at joint E.

Determine the shear at the lower end of the column A using equilibrium conditions.

$∑FX=0SEA+SAE=0$

Substitute 10.16 kN for $SEA$ .

$10.16+SAE=0SAE=−10.16 kNSAE=10.16 kN(←)$

Determine the shear at the end F in the column member BF using the relation.

$SFB=MFBL22$

Substitute $59.58 kN⋅m$ for $MEB$ and 6 m for $L2$ .

$SFB=59.5862=19.86 kN(→)$

The shear at the column memer FB must act towards right, so that it can produce Clockwise moment to balance the counterclockwise moment at joint F.

Determine the shear at the lower end of the column B using equilibrium conditions.

$∑FX=0SFB+SBF=0$

Substitute 19.86 kN for $SEB$ .

$19.86+SBF=0SBF=−19.86 kNSBF=19.86 kN(←)$

Determine the shear at the end G in the column member CG using the relation.

$SGC=MGCL22$

Substitute $59.58 kN⋅m$ for $MGC$ and 6 m for $L2$ .

$SGC=59.5862=19.86 kN(→)$

The shear at the column member GC must act towards right, so that it can produce counterclockwise moment to balance the clockwise moment at joint G.

Determine the shear at the lower end of the column C using equilibrium conditions.

$∑FX=0SGC+SCG=0$

Substitute 19.86 kN for $SGC$ .

$19.86+SCG=0SCG=−19.86 kNSCG=19.86kN(←)$

Determine the shear at the end H in the column member DH using the relation.

$SHD=MHDL22$

Substitute $30.48 kN⋅m$ for $MHD$ and 6 m for $L2$ .

$SHD=30.4862=10.16 kN(→)$

The shear at the column member HD must act towards right, so that it can produce Clockwise moment to balance the counterclockwise moment at joint H.

Determine the shear at the lower end of the column A using equilibrium conditions.

$∑FX=0SHD+SDH=0$

Substitute 10.16 kN for $SHD$ .

$10.16+SDH=0SDH=−10.16 kNSDH=10.16 kN(←)$

Draw the free body diagram of frame with the column moments and shears for the portion EIJ as in Figure (7).

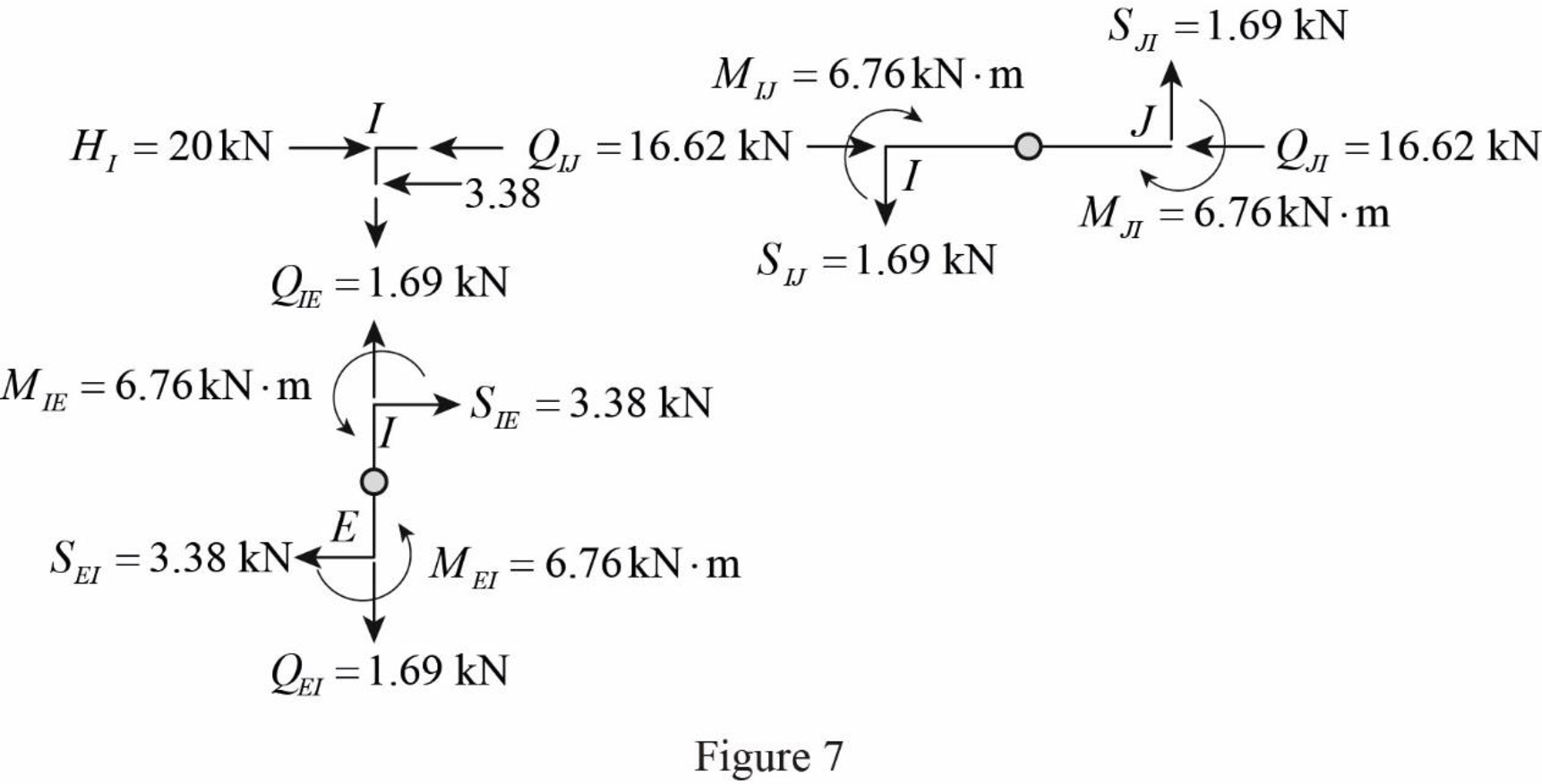
Structural Analysis, Si Edition (mindtap Course List), Chapter 12, Problem 20P , additional homework tip 7

Girder axial forces:

Girder IJ.

Determine the girder end action at the upper left end joint I using the equilibrium condition.

Apply equilibrium condition at left end joint I.

$∑FX=0QIJ−SIE+HI=0$

Substitute3.38 kN for $SIE$ and 20 kN for $HI$ .

$QIJ−3.38+20=0QIJ=−16.62 kNQIJ=16.62 kN(←)$

The girder end action at joint I in the girder IJ is $QIJ=16.62 kN(→)$ .

Determine the girder end action at the upper right end joint H using the equilibrium condition.

Apply equilibrium condition at end joint J.

$∑FX=0QIJ+QJI=0$

Substitute 16.62 kN for $QIJ$ .

$16.62+QJI=0QJI=−16.62 kNQJI=16.62 kN(←)$

Girder JK.

Determine the girder end action at the left end joint J for the girder JK using the relation.

$∑FX=0−QJI+QJK+SJF=0$

Substitute 16.62 kN for $QJI$ and 6.61 kN for $SJF$ .

$−16.62+QJK+6.61=0QJK=10.01 kN(→)$

Determine the girder end action at the right end joint K.

$∑FX=0QJK+QKJ=0$

Substitute 10.01 kN for $QJK$ .

$10.01+QKJ=0QKJ=−10.01 kNQKJ=10.01 kN(←)$

Girder KL.

Determine the girder end action at the left end joint K for the girder KL using the relation.

$∑FX=0−QKJ+QKL+SKG=0$

Substitute 10.01 kN for $QKJ$ and 6.61 kN for $SKG$ .

$−10.01+QKL+6.61=0QKL=3.4 kN(→)$

Determine the girder end action at the right end joint L.

$∑FX=0QKL+QLK=0$

Substitute 3.4 kN for $QKL$ .

$3.4+QLK=0QLK=−3.4 kNQLK=3.4 kN(←)$

Girder EF.

Apply equilibrium condition at left end joint E.

$∑FX=0−QEF−SEA+SEI+HE=0$

Substitute 10.16 kN for $SEA$ , 3.38 kN for $SEI$ , and 40 kN for $HE$ .

$−QEF−10.16+3.38+40=0QEF=−33.22 kNQEF=33.22 kN(←)$

The girder end action at joint E in the girder EF is $QEF=33.22 kN(→)$ .

Determine the girder end action at the right end joint F using the equilibrium condition.

Apply equilibrium condition at left end joint F.

$∑FX=0QEF+QFE=0$

Substitute 33.22 kN for $QEF$ .

$33.22+QFE=0QFE=−33.22 kNQFE=33.22 kN(←)$

Determine the girder end action at the left end joint F for the girder FG using equilibrium condition.

$∑FX=0QFG−QFE+SFB−SFJ=0$

Substitute 33.22 kN for $QFE$ , 19.86 kN for $SFB$ , and 6.61 kN for $SFJ$ .

$QFG−33.22+19.86−6.61=0QFG=19.97 kN(→)$

Determine the girder end action at the right end joint G.

$∑FX=0QFG+QGF=0$

Substitute 19.97 kN for $QFG$ .

$19.97+QGF=0QGF=−19.97 kNQGF=19.97 kN(←)$

Determine the girder end action at the left end joint G for the girder GH using equilibrium condition.

$∑FX=0QGH−QGF+SGC−SGK=0$

Substitute 19.97 kN for $QGF$ , 19.86 kN for $SGC$ , and 6.61 kN for $SGK$ .

$QGH−19.97+19.86−6.61=0QGH=6.72 kN(→)$

Determine the girder end action at the right end joint H.

$∑FX=0QGH+QHG=0$

Substitute 6.72 kN for $QGH$ .

$6.72+QHG=0QHG=−6.72 kNQHG=6.72 kN(←)$

Draw the freebody diagram of the member end forces and moments as in Figure (8).

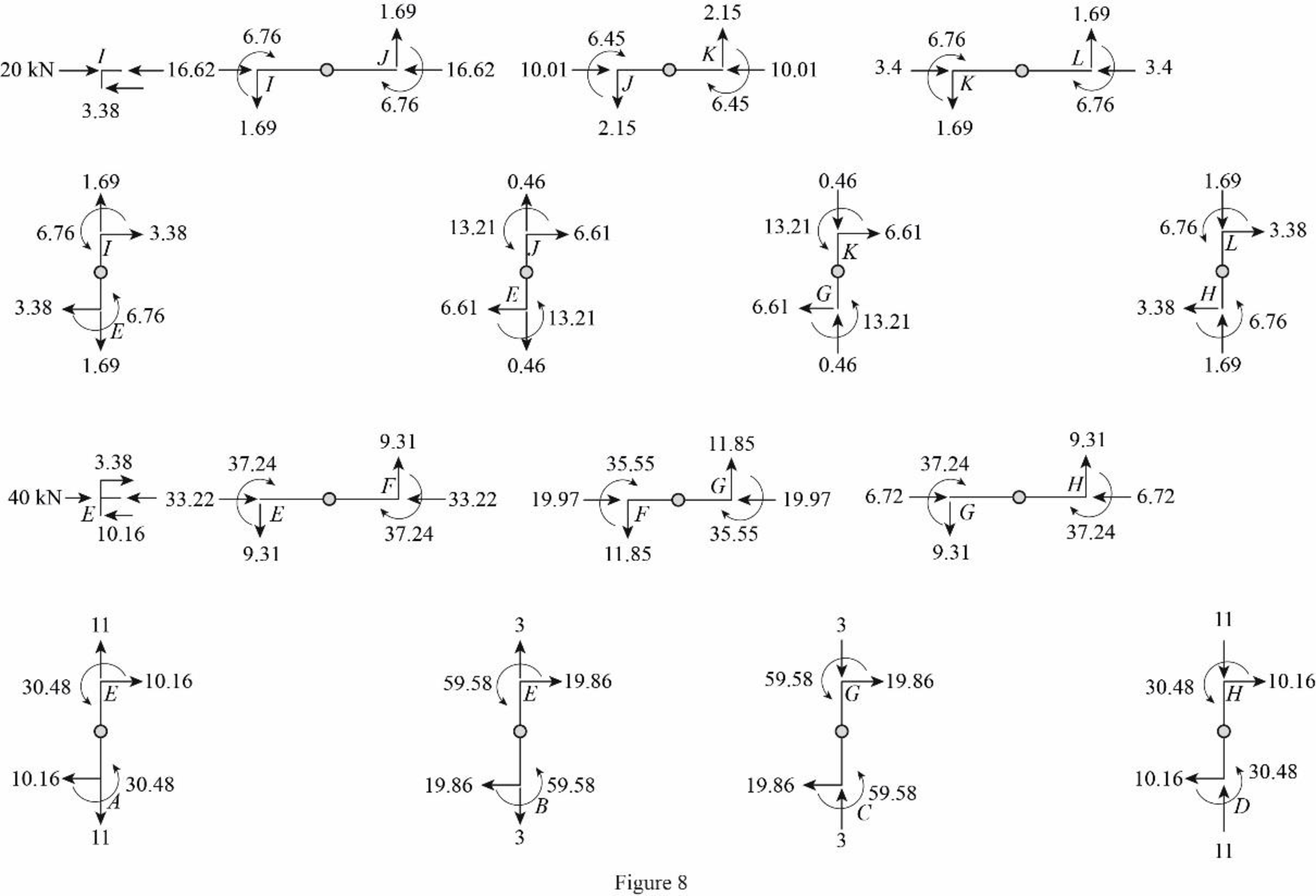
Structural Analysis, Si Edition (mindtap Course List), Chapter 12, Problem 20P , additional homework tip 8

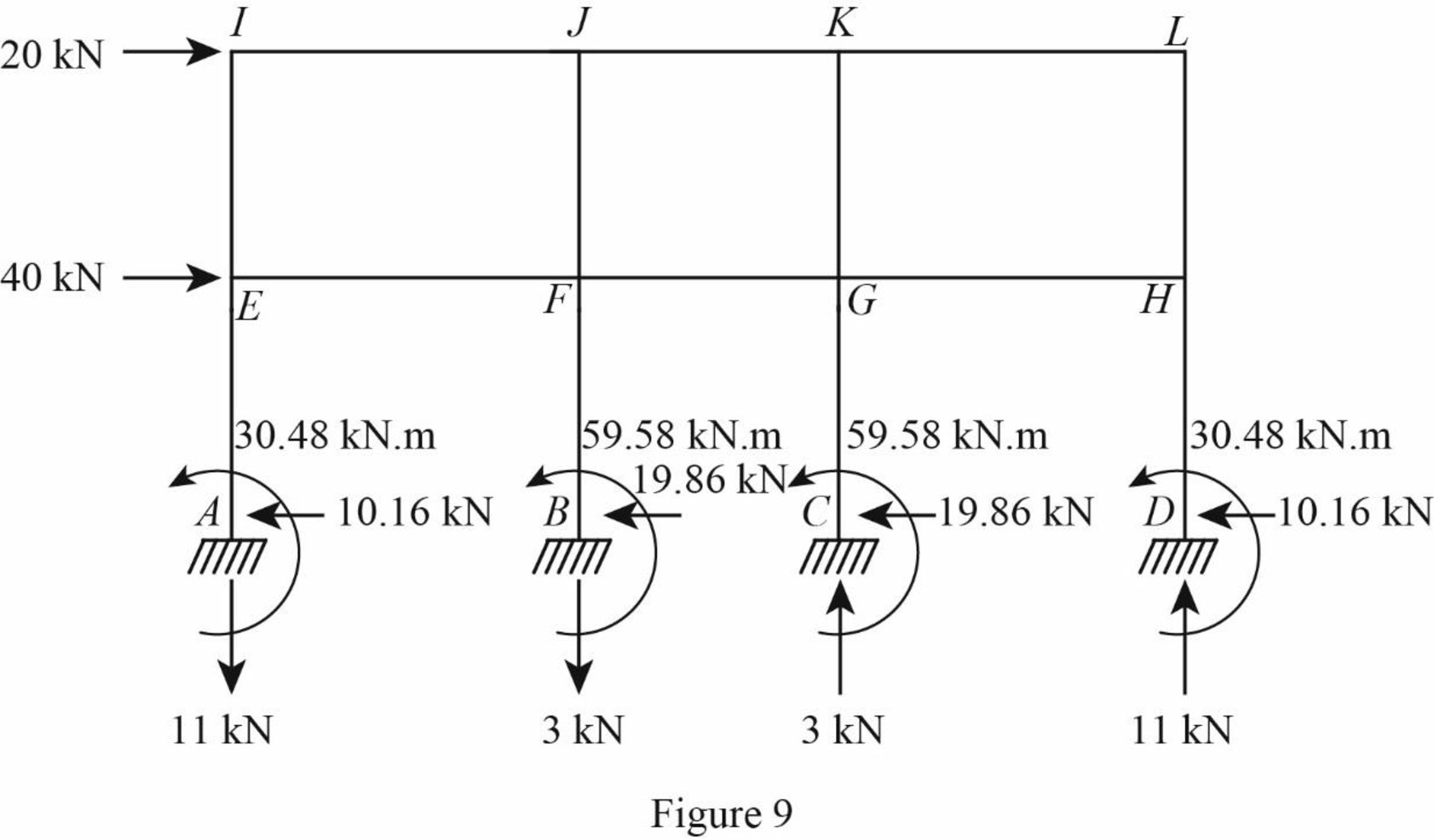
Draw the freebody diagram of the frame with support reactions as in Figure (9).

Structural Analysis, Si Edition (mindtap Course List), Chapter 12, Problem 20P , additional homework tip 9

Want to see more full solutions like this?

Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!

Students have asked these similar questions

Beam ABD is supported and loaded as shown. The cross-section of the beam is also shown. The modulus of elasticity of the beam is 200 GPa. 6.0 kN/m Cross-section: 330 mm 4.5 kN 8.0 kNm 40 mm 2.5 m 1.5 m 20 mm Set up the discontinuity moment function in terms of x. List all the appropriate boundary conditions. Determine the slope function in terms of x. Determine the deflection function in terms of x. Determine the support reactions. Determine the maximum deflection. 290 mm

Draw the Shear Force Diagram and Bending Moment Diagram for the beam shown in Fig.1. The beam is subjected to an UDL of w=65m. L=4.5m L1= 1.8m. Assume the support at C is pinned, and A and B are roller supports. E = 200GPa, I = 250x106 mm4.

Calculate the BMs (bending moments) at all the joints of the beam shown in Fig.1 using the Slope Deflection method. The beam is subjected to an UDL of w=65m. L=4.5m L1= 1.8m. Assume the support at C is pinned, and A and B are roller supports. E = 200GPa, I = 250x106 mm4.

Answer 2