
Concept explainers
The __________is that part of an atom that moves from one atom to another.
A. electron
B. proton
C. neutron
The part of an atom that moves from one atom to another.
Answer to Problem 1RQ
The correct answer is (a) electron.
Explanation of Solution
An atom is the smallest part of a substance that is made up of electron, neutron and protons. The neutrons as the name suggest has no charge, while the protons are positively charged ions and the electrons are negatively chargedions present in the outermost shell moves around the nucleus of an atom. When a sufficient amount of energy or force is applied to an atom, the outer electron become free and can move from one atom to another.
In the given figure, an atom of sodium having excess of electron and another atom of chlorine having a deficiency of electron thus, both the atoms become stable by transferring an electron from sodium atom to chlorine and forming a covalent bond between them.
Thus, the electron is the smallest ion that moves from one atom to another.
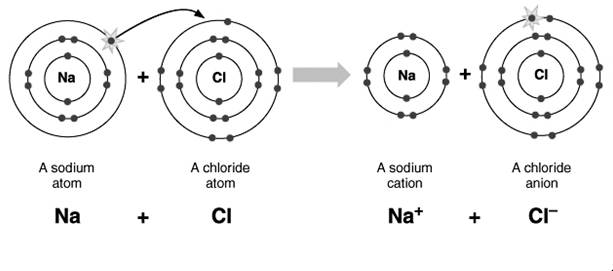
Proton:
The proton being heavier in mass as compared to electron cannot be able to move from one atom to another.
Neutron:
They are found in the nucleus of an atom.
The protons and neutrons stick together in the nucleus of an atom during normal conditions.
Want to see more full solutions like this?
Chapter 12 Solutions
Refrigeration and Air Conditioning Technology (MindTap Course List)
- pls solvearrow_forward+1. 0,63 fin r= 0.051 P The stepped rod in sketch is subjected to a tensile force that varies between 4000 and 7000 lb. The rod has a machined surface finish everywhere except the shoulder area, where a grinding operation has been performed to improve the fatigue resistance of the rod. Using a 99% probability of survival, determine the safety factor for infinite life if the rod is made of AISI 1080 steel, quenched and tempered at 800°c Use the Goodman line. Does the part fail at the fillet? Explainarrow_forwardSolve this problem and show all of the workarrow_forward
- I need drawing solution,draw each one by one no Aiarrow_forwardQu. 17 Compute linear density values for [100] for silver (Ag). Express your answer in nm''. . Round off the answer to three significant figures. Qu. 18 Compute linear density value for [111] direction for silver (Ag). Express your answer in nm'. Round off the answer to three significant figures. Qu. 19 Compute planar density value for (100) plane for chromium (Cr). Express your answer in nm?. Round off the answer to two significant figures. Qu. 20 Compute planar density value for (110) plane for chromium (Cr). Express your answer in nm ≥ to four significant figures. show all work please in material engineeringarrow_forward3-142arrow_forward
- I need solutionsarrow_forward3-137arrow_forwardLarge wind turbines with a power capacity of 8 MW and blade span diameters of over 160 m areavailable for electric power generation. Consider a wind turbine with a blade span diameter of 120m installed at a site subjected to steady winds at 8.25 m/s. Taking the overall efficiency of thewind turbine to be 33 percent and the air density to be 1.25 kg/m3, determine the electric powergenerated by this wind turbine. Also, assuming steady winds of 8.25 m/s during a 24-h period,determine the amount of electric energy and the revenue generated per day for a unit price of$0.08/kWh for electricity.arrow_forward
 Refrigeration and Air Conditioning Technology (Mi...Mechanical EngineeringISBN:9781305578296Author:John Tomczyk, Eugene Silberstein, Bill Whitman, Bill JohnsonPublisher:Cengage Learning
Refrigeration and Air Conditioning Technology (Mi...Mechanical EngineeringISBN:9781305578296Author:John Tomczyk, Eugene Silberstein, Bill Whitman, Bill JohnsonPublisher:Cengage Learning Automotive Technology: A Systems Approach (MindTa...Mechanical EngineeringISBN:9781133612315Author:Jack Erjavec, Rob ThompsonPublisher:Cengage Learning
Automotive Technology: A Systems Approach (MindTa...Mechanical EngineeringISBN:9781133612315Author:Jack Erjavec, Rob ThompsonPublisher:Cengage Learning

