SOBECKI ALEKS ACCESS 360 OLA MATH OUR WR
4th Edition
ISBN: 9781260389739
Author: sobecki
Publisher: MCG
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 12, Problem 1RE
Use this information for Exercises 1–4: the preference ballots for an election for the best speaker in a contest are shown. There are three candidates: Peterson (P), Quintana (Q), and Ross (R).
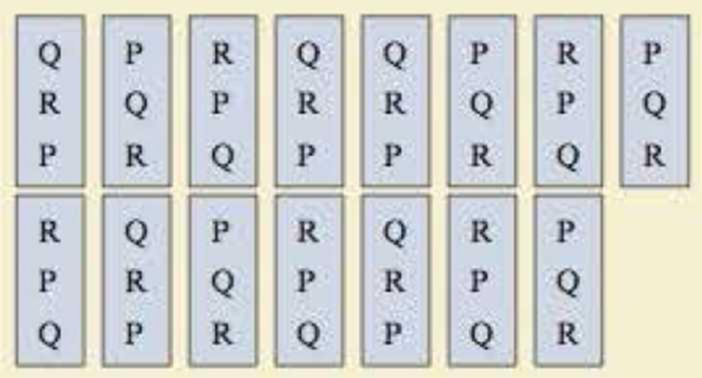
1. Construct a preference table for the results of the election.
Expert Solution & Answer
To determine
To construct: The preference table for the results in the election.
Answer to Problem 1RE
The preference table for the results in the election are listed below.
| Number of votes | 5 | 5 | 5 |
| First choice | Q | P | R |
| Second choice | R | Q | P |
| Third choice | P | R | Q |
Explanation of Solution
Given:
The three candidates are Peterson (P), Quintana (Q) and Ross (R).
The preference table of the best speaker in a contest for the election are listed below.
| Q | P | R | Q | Q | P | R | P | R | Q | P | R | Q | R | P |
| R | Q | P | R | R | Q | P | Q | P | R | Q | P | R | P | Q |
| P | R | Q | P | P | R | Q | R | Q | P | R | Q | P | Q | R |
Calculation:
The choices are Peterson (P), Quintana (Q) and Ross (R).
From the ballot preference table, it is noticed that the candidate order QRP occurs 5 times, the candidate order PQR occurs 5 times and the candidate order RPQ occurs 5 times.
That is, the orders of QRP, PQR and RPQ is 5, 5 and 5.
Therefore, the preference table of the results in the election are listed below.
| Number of votes | 5 | 5 | 5 |
| First choice | Q | P | R |
| Second choice | R | Q | P |
| Third choice | P | R | Q |
Want to see more full solutions like this?
Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Students have asked these similar questions
How to understand and learn Laurent's serial and what's the point
of Laurent's serial
And what are the steps of a smooth solution for Laurent
Not use ai please
Show that any k cyclically consecutive coordinate positions
form an information set.
Chapter 12 Solutions
SOBECKI ALEKS ACCESS 360 OLA MATH OUR WR
Ch. 12.1 - The Student Activities Committee at Camden College...Ch. 12.1 - An election was held for the chairperson of the...Ch. 12.1 - Prob. 3TTOCh. 12.1 - Prob. 4TTOCh. 12.1 - Prob. 1ECh. 12.1 - Prob. 2ECh. 12.1 - Prob. 3ECh. 12.1 - Explain the head-to head comparison criterion.Ch. 12.1 - 5. What is a fairness criterion for an election?
Ch. 12.1 - Prob. 6E
Ch. 12.1 - Prob. 7ECh. 12.1 - Prob. 8ECh. 12.1 - Prob. 9ECh. 12.1 - Prob. 10ECh. 12.1 - Prob. 11ECh. 12.1 - Prob. 12ECh. 12.1 - Prob. 13ECh. 12.1 - Prob. 14ECh. 12.1 - Prob. 15ECh. 12.1 - For Exercises 15–18, rewrite the preference table...Ch. 12.1 - Prob. 17ECh. 12.1 - Prob. 18ECh. 12.1 - Using the election results given in Exercise 9,...Ch. 12.1 - 20. Using the election results given in Exercise...Ch. 12.1 - Prob. 21ECh. 12.1 - Prob. 22ECh. 12.1 - Using the Internet as a resource, look up the...Ch. 12.1 - Suppose that an election has seven candidates, and...Ch. 12.1 - Prob. 25ECh. 12.1 - Prob. 26ECh. 12.1 - Prob. 27ECh. 12.1 - Prob. 28ECh. 12.1 - Prob. 29ECh. 12.1 - Prob. 30ECh. 12.1 - Prob. 31ECh. 12.1 - Prob. 32ECh. 12.2 - Prob. 1TTOCh. 12.2 - Prob. 2TTOCh. 12.2 - Prob. 3TTOCh. 12.2 - If the one voter who listed softball last in the...Ch. 12.2 - Prob. 1ECh. 12.2 - Prob. 2ECh. 12.2 - Prob. 3ECh. 12.2 - Prob. 4ECh. 12.2 - Prob. 5ECh. 12.2 - Can a candidate that gets the least first-place...Ch. 12.2 - A gaming club holds a vote to decide what type of...Ch. 12.2 - The McKees Point Yacht Club Board of Directors...Ch. 12.2 - Prob. 9ECh. 12.2 - A local police union is holding an election for a...Ch. 12.2 - Students at a college were asked to rank three...Ch. 12.2 - Prob. 12ECh. 12.2 - Prob. 13ECh. 12.2 - Prob. 14ECh. 12.2 - Prob. 15ECh. 12.2 - Prob. 16ECh. 12.2 - Prob. 17ECh. 12.2 - Does the election in Exercise 12 violate the...Ch. 12.2 - An English department is voting for a new...Ch. 12.2 - The Association of Self-Employed Working Persons...Ch. 12.2 - Prob. 21ECh. 12.2 - Prob. 22ECh. 12.2 - Suppose that all 4 voters from the last column of...Ch. 12.2 - Suppose that 2 of the 4 voters from the second...Ch. 12.2 - If 2 of the voters from column 1 in Exercise 21...Ch. 12.2 - If the 3 voters in column 4 in Exercise 22 change...Ch. 12.2 - Construct a preference table for an election...Ch. 12.2 - Construct a preference table for an election...Ch. 12.2 - Construct a preference table for an election so...Ch. 12.2 - If the candidates on a preference ballot are...Ch. 12.2 - If the candidates on a preference ballot are...Ch. 12.2 - In an election with four candidates, how many...Ch. 12.2 - Based on your answers to Exercise 32, explain why...Ch. 12.2 - One way to avoid the issue described in Exercises...Ch. 12.2 - Lets talk about a modified Borda count method....Ch. 12.3 - Prob. 1TTOCh. 12.3 - Prob. 2TTOCh. 12.3 - Does the election in Try This One 2 violate the...Ch. 12.3 - Prob. 4TTOCh. 12.3 - Explain how to determine the winner of an election...Ch. 12.3 - Prob. 2ECh. 12.3 - Describe Arrows impossibility theorem. How is it...Ch. 12.3 - Prob. 4ECh. 12.3 - Prob. 5ECh. 12.3 - Which of the five voting methods we studied do you...Ch. 12.3 - If all of the voters in an approval voting...Ch. 12.3 - Fill in the table below, which summarizes our five...Ch. 12.3 - Prob. 9ECh. 12.3 - Prob. 10ECh. 12.3 - Prob. 11ECh. 12.3 - Prob. 12ECh. 12.3 - Prob. 13ECh. 12.3 - Prob. 14ECh. 12.3 - Prob. 15ECh. 12.3 - Prob. 16ECh. 12.3 - The McKees Point Yacht Club Board of Directors...Ch. 12.3 - The students in Dr. Lees math class are asked to...Ch. 12.3 - If Professor Donovan was unable to serve as...Ch. 12.3 - If the travel company from Exercise 14 loses its...Ch. 12.3 - If the West Oak Golf Club is unavailable and the...Ch. 12.3 - If a room for Dr. Lees final exam was not...Ch. 12.3 - A sports committee of students needs to choose a...Ch. 12.3 - Prob. 24ECh. 12.3 - Prob. 25ECh. 12.3 - Prob. 26ECh. 12.3 - Prob. 27ECh. 12.3 - Prob. 28ECh. 12.3 - Prob. 29ECh. 12.3 - Construct a preference table so that one candidate...Ch. 12.3 - Prob. 31ECh. 12.3 - Prob. 32ECh. 12.3 - Prob. 33ECh. 12.3 - Evaluate each voting method we studied if there...Ch. 12.3 - Suppose that in an election for city council,...Ch. 12.3 - Prob. 36ECh. 12.3 - Devise a method for breaking ties when using...Ch. 12.3 - Prob. 38ECh. 12.4 - Prob. 1TTOCh. 12.4 - Prob. 2TTOCh. 12.4 - Prob. 3TTOCh. 12.4 - Prob. 4TTOCh. 12.4 - Prob. 5TTOCh. 12.4 - Assign the 30 seats from Try This One 5 using...Ch. 12.4 - Prob. 7TTOCh. 12.4 - Prob. 8TTOCh. 12.4 - Prob. 1ECh. 12.4 - Prob. 2ECh. 12.4 - Prob. 3ECh. 12.4 - Describe how to find the upper and lower quotas...Ch. 12.4 - Prob. 5ECh. 12.4 - Prob. 6ECh. 12.4 - Prob. 7ECh. 12.4 - Prob. 8ECh. 12.4 - Prob. 9ECh. 12.4 - Prob. 10ECh. 12.4 - In Exercises 912, find the standard divisor for...Ch. 12.4 - Prob. 12ECh. 12.4 - Prob. 13ECh. 12.4 - Prob. 14ECh. 12.4 - Prob. 15ECh. 12.4 - Prob. 16ECh. 12.4 - Prob. 17ECh. 12.4 - Prob. 18ECh. 12.4 - Prob. 19ECh. 12.4 - Prob. 20ECh. 12.4 - Prob. 21ECh. 12.4 - Prob. 22ECh. 12.4 - Prob. 23ECh. 12.4 - Prob. 24ECh. 12.4 - Prob. 25ECh. 12.4 - For Exercises 2628 find: (a)The standard divisor....Ch. 12.4 - Prob. 27ECh. 12.4 - Prob. 28ECh. 12.4 - Prob. 29ECh. 12.4 - Prob. 30ECh. 12.4 - Prob. 31ECh. 12.4 - Prob. 32ECh. 12.4 - Prob. 33ECh. 12.4 - Prob. 34ECh. 12.4 - Prob. 35ECh. 12.4 - Prob. 36ECh. 12.4 - Prob. 37ECh. 12.4 - Prob. 38ECh. 12.4 - Prob. 39ECh. 12.4 - Prob. 40ECh. 12.4 - Prob. 41ECh. 12.4 - Prob. 42ECh. 12.4 - Prob. 43ECh. 12.5 - Prob. 1TTOCh. 12.5 - Try This One 2
A county with three districts has...Ch. 12.5 - Prob. 3TTOCh. 12.5 - Prob. 1ECh. 12.5 - Prob. 2ECh. 12.5 - Prob. 3ECh. 12.5 - Prob. 4ECh. 12.5 - What is the quota rule? Which apportionment...Ch. 12.5 - Prob. 6ECh. 12.5 - Prob. 7ECh. 12.5 - Prob. 8ECh. 12.5 - Prob. 9ECh. 12.5 - Prob. 10ECh. 12.5 - Prob. 11ECh. 12.5 - Prob. 12ECh. 12.5 - The table shows the enrollment at two campuses of...Ch. 12.5 - Prob. 14ECh. 12.5 - Prob. 15ECh. 12.5 - Prob. 16ECh. 12.5 - Write an essay explaining why many people feel...Ch. 12.5 - 18. Which do you think is more serious: violating...Ch. 12 - Use this information for Exercises 14: the...Ch. 12 - Use this information for Exercises 14: the...Ch. 12 - Use this information for Exercises 14: the...Ch. 12 - Prob. 4RECh. 12 - Prob. 5RECh. 12 - Prob. 6RECh. 12 - Prob. 7RECh. 12 - Prob. 8RECh. 12 - Prob. 9RECh. 12 - Prob. 10RECh. 12 - Prob. 11RECh. 12 - Prob. 12RECh. 12 - Prob. 13RECh. 12 - Prob. 14RECh. 12 - Use this information for Exercises 917: a large...Ch. 12 - Prob. 16RECh. 12 - Use this information for Exercises 917: a large...Ch. 12 - Prob. 18RECh. 12 - Prob. 19RECh. 12 - Prob. 20RECh. 12 - Prob. 21RECh. 12 - Prob. 22RECh. 12 - Prob. 23RECh. 12 - Prob. 24RECh. 12 - Prob. 25RECh. 12 - Prob. 26RECh. 12 - Prob. 27RECh. 12 - Prob. 28RECh. 12 - Prob. 29RECh. 12 - A community college bought 15 laptop computers to...Ch. 12 - Prob. 31RECh. 12 - Prob. 32RECh. 12 - Prob. 33RECh. 12 - Prob. 34RECh. 12 - Prob. 35RECh. 12 - Repeat exercise 30 using the Huntington-Hill...Ch. 12 - Prob. 37RECh. 12 - Prob. 38RECh. 12 - Prob. 39RECh. 12 - Prob. 40RECh. 12 - Prob. 41RECh. 12 - Prob. 42RECh. 12 - Prob. 43RECh. 12 - Prob. 1CTCh. 12 - Prob. 2CTCh. 12 - Prob. 3CTCh. 12 - Prob. 4CTCh. 12 - Prob. 5CTCh. 12 - Prob. 6CTCh. 12 - Prob. 7CTCh. 12 - Prob. 8CTCh. 12 - Use this information for Exercises 512: a small...Ch. 12 - Prob. 10CTCh. 12 - Prob. 11CTCh. 12 - Prob. 12CTCh. 12 - Prob. 13CTCh. 12 - An airline offers nonstop flights from Fort...Ch. 12 - Prob. 15CTCh. 12 - Repeat Problem 14 using Websters method.Ch. 12 - Repeat Problem 14 using the Huntington-Hill...Ch. 12 - Prob. 18CTCh. 12 - Prob. 19CTCh. 12 - Prob. 20CTCh. 12 - Prob. 21CT
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- This box plot represents the score out of 90 received by students on a driver's education exam. 75% of the students passed the exam. What is the minimum score needed to pass the exam? Submitting x and Whickers Graph Low 62, C 62 66 70 74 78 82 86 90 Driver's education exam score (out of 90)arrow_forwardExample: If ƒ (x + 2π) = ƒ (x), find the Fourier expansion f(x) = eax in the interval [−π,π]arrow_forwardPlease can you give detailed steps on how the solutions change from complex form to real form. Thanks.arrow_forward
- Examples: Solve the following differential equation using Laplace transform (e) ty"-ty+y=0 with y(0) = 0, and y'(0) = 1arrow_forwardExamples: Solve the following differential equation using Laplace transform (a) y" +2y+y=t with y(0) = 0, and y'(0) = 1arrow_forwardTemperature for Sudbury (degrees Celsius) 3. The following table gives the mean monthly temperatures for Sudbury, Ontario and Windsor, Ontario. Each month is represented by the day of the year in the middle of the month. Month Day of Year Temperature for Windsor (degrees Celsius) January 15 -13.7 -4.7 February 45 -11.9 -3.8 March 75 -5.9 2.3 April 106 3.0 8.7 May 136 10.6 14.6 June 167 15.8 20.2 July 197 18.9 22.6 August 228 17.4 22.0 September 259 12.2 17.9 October 289 6.2 11.5 November 320 -1.2 4.8 December 350 -10.1 -1.2 a) Create a scatter plot of temperature vs. day of the year for each city. b) Draw the curve of best fit for each graph. c) Use your graphs to estimate when the temperature increases fastest, for each set of temperature data. Explain how you determined these values. d) Use your graphs to estimate the rate at which the temperature is increasing at the two times from question 3. e) Determine an equation of a sinusoidal function to model the data for each cityarrow_forward
Recommended textbooks for you
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
12. Searching and Sorting; Author: MIT OpenCourseWare;https://www.youtube.com/watch?v=6LOwPhPDwVc;License: Standard YouTube License, CC-BY
Algorithms and Data Structures - Full Course for Beginners from Treehouse; Author: freeCodeCamp.org;https://www.youtube.com/watch?v=8hly31xKli0;License: Standard Youtube License