
EP THOMAS'CALCULUS,EARLY TRANS.-MYLAB
14th Edition
ISBN: 9780135961308
Author: Hass
Publisher: PEARSON CO
expand_more
expand_more
format_list_bulleted
Question
Chapter 12, Problem 1GYR
To determine
Explain how the directed line segment in the plane represent the same
Expert Solution & Answer
Explanation of Solution
Description:
Generally, the vector is signified by the directed line segment
Figure 1 shows the directed line segment in the plane represent the same vector.
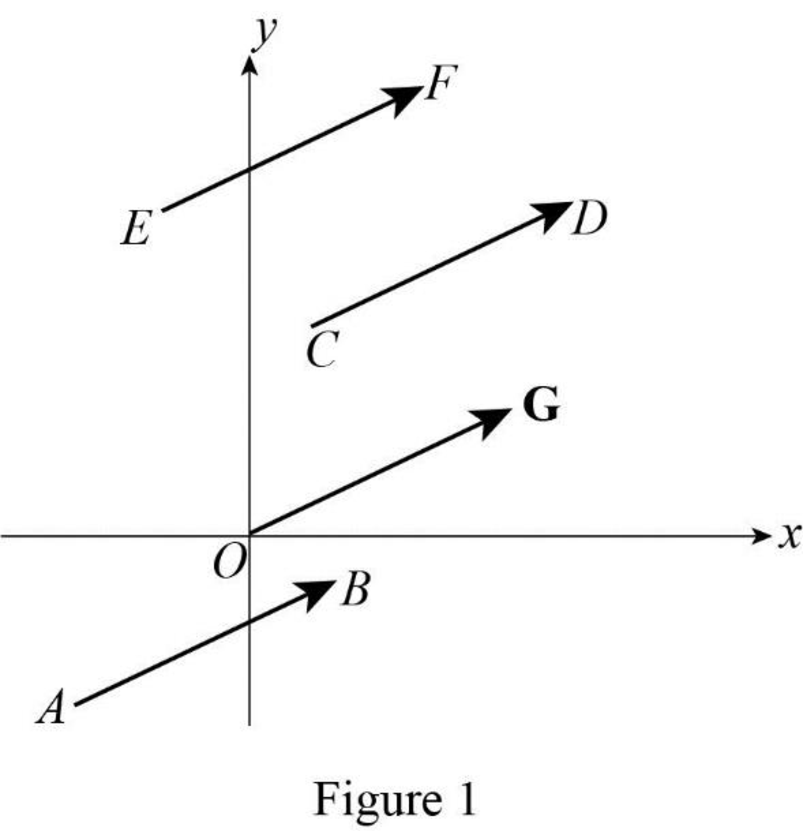
In Figure 1, the four arrows represent in the plane is the directed line segment having the same length and direction. Therefore, the directed line segment can be written as follows.
Thus, the directed line segment in the plane represent the same vector is explained.
Want to see more full solutions like this?
Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Students have asked these similar questions
do question 2 please
question 10 please
00
(a) Starting with the geometric series Σ X^, find the sum of the series
n = 0
00
Σηχη - 1,
|x| < 1.
n = 1
(b) Find the sum of each of the following series.
00
Σnx",
n = 1
|x| < 1
(ii)
n = 1
sin
(c) Find the sum of each of the following series.
(i)
00
Σn(n-1)x^, |x| <1
n = 2
(ii)
00
n = 2
n²
- n
4n
(iii)
M8
n = 1
շո
Chapter 12 Solutions
EP THOMAS'CALCULUS,EARLY TRANS.-MYLAB
Ch. 12.1 - In Exercises 1–16, give a geometric description of...Ch. 12.1 - In Exercises 1–16, give a geometric description of...Ch. 12.1 - In Exercises 1–16, give a geometric description of...Ch. 12.1 - In Exercises 1–16, give a geometric description of...Ch. 12.1 - In Exercises 1–16, give a geometric description of...Ch. 12.1 - In Exercises 1–16, give a geometric description of...Ch. 12.1 - In Exercises 1–16, give a geometric description of...Ch. 12.1 - In Exercises 1–16, give a geometric description of...Ch. 12.1 - In Exercises 1–16, give a geometric description of...Ch. 12.1 - In Exercises 1–16, give a geometric description of...
Ch. 12.1 - In Exercises 1–16, give a geometric description of...Ch. 12.1 - In Exercises 1–16, give a geometric description of...Ch. 12.1 - In Exercises 1–16, give a geometric description of...Ch. 12.1 - In Exercises 1–16, give a geometric description of...Ch. 12.1 - In Exercises 1–16, give a geometric description of...Ch. 12.1 - In Exercises 1–16, give a geometric description of...Ch. 12.1 - In Exercises 17–24, describe the sets of points in...Ch. 12.1 - In Exercises 17–24, describe the sets of points in...Ch. 12.1 - In Exercises 17–24, describe the sets of points in...Ch. 12.1 - In Exercises 17–24, describe the sets of points in...Ch. 12.1 - In Exercises 17–24, describe the sets of points in...Ch. 12.1 - In Exercises 17–24, describe the sets of points in...Ch. 12.1 - In Exercises 17–24, describe the sets of points in...Ch. 12.1 - In Exercises 17–24, describe the sets of points in...Ch. 12.1 - In Exercises 25–30, find the distance between...Ch. 12.1 - In Exercises 25–30, find the distance between...Ch. 12.1 - In Exercises 25–30, find the distance between...Ch. 12.1 - In Exercises 25–30, find the distance between...Ch. 12.1 - In Exercises 25–30, find the distance between...Ch. 12.1 - In Exercises 25–30, find the distance between...Ch. 12.1 - Find the distance from the point (3, −4, 2) to...Ch. 12.1 - Find the distance from the point (−2, 1, 4) to...Ch. 12.1 - Find the distance from the point (4, 3, 0) to...Ch. 12.1 - Find the distance from the
x-axis to the plane z =...Ch. 12.1 - In Exercises 35–14, describe the given set with a...Ch. 12.1 - In Exercises 35–44, describe the given set with a...Ch. 12.1 - In Exercises 35–44, describe the given set with a...Ch. 12.1 - In Exercises 35–44, describe the given set with a...Ch. 12.1 - In Exercises 35–44, describe the given set with a...Ch. 12.1 - In Exercises 35–44, describe the given set with a...Ch. 12.1 - In Exercises 35–14, describe the given set with a...Ch. 12.1 - The set of points in space equidistant from the...Ch. 12.1 - Prob. 43ECh. 12.1 - In Exercises 35–44, describe the given set with a...Ch. 12.1 - Prob. 45ECh. 12.1 - Write inequalities to describe the sets in...Ch. 12.1 - Prob. 47ECh. 12.1 - Prob. 48ECh. 12.1 - Prob. 49ECh. 12.1 - Prob. 50ECh. 12.1 - Find the center C and the radius a for the sphere...Ch. 12.1 - Prob. 52ECh. 12.1 - Find the center C and the radius a for the sphere...Ch. 12.1 - Prob. 54ECh. 12.1 - Find the center C and the radius a for the sphere...Ch. 12.1 - Prob. 56ECh. 12.1 - Find the center C and the radius a for the sphere...Ch. 12.1 - Find the center C and the radius a for the sphere...Ch. 12.1 - Find the center C and the radius a for the sphere...Ch. 12.1 - Find the center C and the radius a for the sphere...Ch. 12.1 - Find equations for the sphere whose centers and...Ch. 12.1 - Find equations for the sphere whose centers and...Ch. 12.1 - Find equations for the sphere whose centers and...Ch. 12.1 - Prob. 64ECh. 12.1 - Prob. 65ECh. 12.1 - Prob. 66ECh. 12.1 - Prob. 67ECh. 12.1 - Prob. 68ECh. 12.1 - Prob. 69ECh. 12.1 - Prob. 70ECh. 12.1 - Prob. 71ECh. 12.1 - Prob. 72ECh. 12.1 - Prob. 73ECh. 12.1 - Prob. 74ECh. 12.1 - Prob. 75ECh. 12.1 - Find all points that simultaneously lie 3 units...Ch. 12.2 - In Exercises 1–8, let u = 〈3, −2〉 and v = 〈−2, 5〉....Ch. 12.2 - Prob. 2ECh. 12.2 - In Exercises 1–8, let u = 〈3, −2〉 and v = 〈−2, 5〉....Ch. 12.2 - Prob. 4ECh. 12.2 - In Exercises 1–8, let u = 〈3, −2〉 and v = 〈−2, 5〉....Ch. 12.2 - Prob. 6ECh. 12.2 - In Exercises 1–8, let u = 〈3, −2〉 and v = 〈−2, 5〉....Ch. 12.2 - Prob. 8ECh. 12.2 - Prob. 9ECh. 12.2 - In Exercises 9–16, find the component form of the...Ch. 12.2 - Prob. 11ECh. 12.2 - Prob. 12ECh. 12.2 - The unit vector that makes an angle θ = 2π/3 with...Ch. 12.2 - Prob. 14ECh. 12.2 - The unit vector obtained by rotating the vector ...Ch. 12.2 - The unit vector obtained by rotating the vector ...Ch. 12.2 - Prob. 17ECh. 12.2 - Prob. 18ECh. 12.2 - Prob. 19ECh. 12.2 - Prob. 20ECh. 12.2 - In Exercises 17–22, express each vector in the...Ch. 12.2 - Prob. 22ECh. 12.2 - In Exercises 23 and 24, copy vectors u, v, and w...Ch. 12.2 - In Exercises 23 and 24, copy vectors u, v, and w...Ch. 12.2 - Prob. 25ECh. 12.2 - Prob. 26ECh. 12.2 - Prob. 27ECh. 12.2 - In Exercises 25–30, express each vector as a...Ch. 12.2 - Prob. 29ECh. 12.2 - In Exercises 25–30, express each vector as a...Ch. 12.2 - Find the vectors whose lengths and directions are...Ch. 12.2 - Prob. 32ECh. 12.2 - Prob. 33ECh. 12.2 - Prob. 34ECh. 12.2 - In Exercises 35–38, find a. the direction of and...Ch. 12.2 - Prob. 36ECh. 12.2 - In Exercises 35–38, find a. the direction of and...Ch. 12.2 - Prob. 38ECh. 12.2 - Prob. 39ECh. 12.2 - If = −7i + 3j + 8k and A is the point (−2, −3,...Ch. 12.2 - Prob. 41ECh. 12.2 - Prob. 42ECh. 12.2 - Prob. 43ECh. 12.2 - Linear combination Let u = ⟨1, 2, 2 ⟩, v = ⟨ 1,...Ch. 12.2 - Velocity An airplane is flying in the direction...Ch. 12.2 - (Continuation of Example 8.) What speed and...Ch. 12.2 - Prob. 47ECh. 12.2 - Consider a 50-N weight suspended by two wires as...Ch. 12.2 - Consider a w-N weight suspended by two wires as...Ch. 12.2 - Consider a 25-N weight suspended by two wires as...Ch. 12.2 - Location A bird flies from its nest 5 km in the...Ch. 12.2 - Use similar triangles to find the coordinates of...Ch. 12.2 - Prob. 53ECh. 12.2 - Prob. 54ECh. 12.2 - Prob. 55ECh. 12.2 - Prob. 56ECh. 12.2 - Prob. 57ECh. 12.2 - Prob. 58ECh. 12.2 - Prob. 59ECh. 12.3 - Prob. 1ECh. 12.3 - 2. v = (3/5)i + (4/5)k, u = 5i + 12j
v · u, |v|,...Ch. 12.3 - Prob. 3ECh. 12.3 - Prob. 4ECh. 12.3 - 5. v = 5j – 3k, u = i + j + k
v · u, |v|, |u|
the...Ch. 12.3 - Prob. 6ECh. 12.3 - Prob. 7ECh. 12.3 -
v · u, | v |, | u |
the cosine of the angle...Ch. 12.3 - Find the angles between the vectors in Exercises...Ch. 12.3 - Prob. 10ECh. 12.3 - Prob. 11ECh. 12.3 - Prob. 12ECh. 12.3 - Prob. 13ECh. 12.3 - Rectangle Find the measures of the angles between...Ch. 12.3 - Direction angles and direction cosines The...Ch. 12.3 - Prob. 16ECh. 12.3 - Prob. 17ECh. 12.3 - Prob. 18ECh. 12.3 - Prob. 19ECh. 12.3 - Prob. 20ECh. 12.3 - Prob. 21ECh. 12.3 - Prob. 22ECh. 12.3 - When parallelograms are rectangles Prove that a...Ch. 12.3 - Prob. 24ECh. 12.3 - Prob. 25ECh. 12.3 - Prob. 26ECh. 12.3 - Prob. 27ECh. 12.3 - Prob. 28ECh. 12.3 - Prob. 29ECh. 12.3 - Prob. 30ECh. 12.3 - Prob. 31ECh. 12.3 - Prob. 32ECh. 12.3 - Prob. 33ECh. 12.3 - Prob. 34ECh. 12.3 - Prob. 35ECh. 12.3 - Prob. 36ECh. 12.3 - Prob. 37ECh. 12.3 - Prob. 38ECh. 12.3 - Prob. 39ECh. 12.3 - Prob. 40ECh. 12.3 - Prob. 41ECh. 12.3 - Prob. 42ECh. 12.3 - Prob. 43ECh. 12.3 - Prob. 44ECh. 12.3 - Prob. 45ECh. 12.3 - Prob. 46ECh. 12.3 - Prob. 47ECh. 12.3 - Prob. 48ECh. 12.3 - Prob. 49ECh. 12.3 - Prob. 50ECh. 12.3 - Prob. 51ECh. 12.3 - Prob. 52ECh. 12.4 - In Exercises 1–8, find the length and direction...Ch. 12.4 - Prob. 2ECh. 12.4 - Prob. 3ECh. 12.4 - In Exercises 1–8, find the length and direction...Ch. 12.4 - In Exercises 1–8, find the length and direction...Ch. 12.4 - In Exercises 1–8, find the length and direction...Ch. 12.4 - In Exercises 1–8, find the length and direction...Ch. 12.4 - In Exercises 1–8, find the length and direction...Ch. 12.4 - In Exercises 9–14, sketch the coordinate axes and...Ch. 12.4 - In Exercises 9–14, sketch the coordinate axes and...Ch. 12.4 - In Exercises 9–14, sketch the coordinate axes and...Ch. 12.4 - In Exercises 9–14, sketch the coordinate axes and...Ch. 12.4 - In Exercises 9–14, sketch the coordinate axes and...Ch. 12.4 - In Exercises 9–14, sketch the coordinate axes and...Ch. 12.4 - In Exercises 15−18,
Find the area of the triangle...Ch. 12.4 - In Exercises 15−18,
Find the area of the triangle...Ch. 12.4 - Prob. 17ECh. 12.4 - In Exercises 15−18,
Find the area of the triangle...Ch. 12.4 - In Exercises 19–22, verify that (u × v) · w = (v ×...Ch. 12.4 - In Exercises 19–22, verify that (u × v) · w = (v ×...Ch. 12.4 - In Exercises 19–22, verify that (u × v) · w = (v ×...Ch. 12.4 - In Exercises 19–22, verify that (u × v) · w = (v ×...Ch. 12.4 - Prob. 23ECh. 12.4 - Prob. 24ECh. 12.4 - In Exercises 25 and 26, find the magnitude of the...Ch. 12.4 - In Exercises 25 and 26, find the magnitude of the...Ch. 12.4 - Which of the following are always true, and which...Ch. 12.4 - Which of the following are always true, and which...Ch. 12.4 - Given nonzero vectors u, v, and w, use dot product...Ch. 12.4 - Prob. 30ECh. 12.4 - Prob. 31ECh. 12.4 - Prob. 32ECh. 12.4 - Prob. 33ECh. 12.4 - Prob. 34ECh. 12.4 - Find the areas of the parallelograms whose...Ch. 12.4 - Find the areas of the parallelograms whose...Ch. 12.4 - Find the areas of the parallelograms whose...Ch. 12.4 - Find the areas of the parallelograms whose...Ch. 12.4 - Find the areas of the parallelograms whose...Ch. 12.4 - Find the areas of the parallelograms whose...Ch. 12.4 - Find the areas of the triangles whose vertices are...Ch. 12.4 - Find the areas of the triangles whose vertices are...Ch. 12.4 - Find the areas of the triangles whose vertices are...Ch. 12.4 - Find the areas of the triangles whose vertices are...Ch. 12.4 - Find the areas of the triangles whose vertices are...Ch. 12.4 - Find the areas of the triangles whose vertices are...Ch. 12.4 - Find the areas of the triangles whose vertices are...Ch. 12.4 - Find the volume of a parallelepiped with one of...Ch. 12.4 - Triangle area Find a 2 × 2 determinant formula for...Ch. 12.4 - Triangle area Find a concise 3 × 3 determinant...Ch. 12.4 - Using the methods of Section 6.1, where volume is...Ch. 12.4 - Using the methods of Section 6.1, where volume is...Ch. 12.4 - Using the methods of Section 6.1, where volume is...Ch. 12.4 - Using the methods of Section 6.1, where volume is...Ch. 12.4 - In Exercises 55–57, determine whether the given...Ch. 12.4 - In Exercises 55–57, determine whether the given...Ch. 12.4 - Prob. 57ECh. 12.5 - Find parametric equations for the lines in...Ch. 12.5 - Find parametric equations for the lines in...Ch. 12.5 - Find parametric equations for the lines in...Ch. 12.5 - Find parametric equations for the lines in...Ch. 12.5 - Find parametric equations for the lines in...Ch. 12.5 - Find parametric equations for the lines in...Ch. 12.5 - Prob. 7ECh. 12.5 - Prob. 8ECh. 12.5 - Prob. 9ECh. 12.5 - Prob. 10ECh. 12.5 - Prob. 11ECh. 12.5 - Prob. 12ECh. 12.5 - Prob. 13ECh. 12.5 - Prob. 14ECh. 12.5 - Prob. 15ECh. 12.5 - Prob. 16ECh. 12.5 - Prob. 17ECh. 12.5 - Prob. 18ECh. 12.5 - Prob. 19ECh. 12.5 - Prob. 20ECh. 12.5 - Prob. 21ECh. 12.5 - Find equations for the planes in Exercises...Ch. 12.5 - Planes
Find equations for the planes in Exercises...Ch. 12.5 - Prob. 24ECh. 12.5 - Prob. 25ECh. 12.5 - Prob. 26ECh. 12.5 - Prob. 27ECh. 12.5 - Prob. 28ECh. 12.5 - Prob. 29ECh. 12.5 - Prob. 30ECh. 12.5 - Prob. 31ECh. 12.5 - Prob. 32ECh. 12.5 - Prob. 33ECh. 12.5 - Prob. 34ECh. 12.5 - Prob. 35ECh. 12.5 - Prob. 36ECh. 12.5 - Prob. 37ECh. 12.5 - Prob. 38ECh. 12.5 - Prob. 39ECh. 12.5 - Prob. 40ECh. 12.5 - Prob. 41ECh. 12.5 - Prob. 42ECh. 12.5 - Prob. 43ECh. 12.5 - Prob. 44ECh. 12.5 - Prob. 45ECh. 12.5 - Prob. 46ECh. 12.5 - Prob. 47ECh. 12.5 - Prob. 48ECh. 12.5 - Prob. 49ECh. 12.5 - Prob. 50ECh. 12.5 - Prob. 51ECh. 12.5 - Prob. 52ECh. 12.5 - Prob. 53ECh. 12.5 - Prob. 54ECh. 12.5 - Prob. 55ECh. 12.5 - Prob. 56ECh. 12.5 - Prob. 57ECh. 12.5 - Prob. 58ECh. 12.5 - In Exercises 57–60, find the point in which the...Ch. 12.5 - Prob. 60ECh. 12.5 - Find parametrizations for the lines in which the...Ch. 12.5 - Find parametrizations for the lines in which the...Ch. 12.5 - Find parametrizations for the lines in which the...Ch. 12.5 - Prob. 64ECh. 12.5 - Prob. 65ECh. 12.5 - Prob. 66ECh. 12.5 - Prob. 67ECh. 12.5 - Prob. 68ECh. 12.5 - Prob. 69ECh. 12.5 - Prob. 70ECh. 12.5 - Prob. 71ECh. 12.5 - Prob. 72ECh. 12.5 - Prob. 73ECh. 12.5 - Prob. 74ECh. 12.5 - Prob. 75ECh. 12.5 - Prob. 76ECh. 12.5 - Prob. 77ECh. 12.5 - Prob. 78ECh. 12.6 - In Exercises 1–12, match the equation with the...Ch. 12.6 - In Exercises 1–12, match the equation with the...Ch. 12.6 - In Exercises 1–12, match the equation with the...Ch. 12.6 - In Exercises 1–12, match the equation with the...Ch. 12.6 - In Exercises 1–12, match the equation with the...Ch. 12.6 - In Exercises 1–12, match the equation with the...Ch. 12.6 - In Exercises 1–12, match the equation with the...Ch. 12.6 - In Exercises 1–12, match the equation with the...Ch. 12.6 - Prob. 9ECh. 12.6 - Prob. 10ECh. 12.6 - Prob. 11ECh. 12.6 - Prob. 12ECh. 12.6 - Drawing
Sketch the surfaces in Exercises...Ch. 12.6 - Drawing
Sketch the surfaces in Exercises...Ch. 12.6 - Drawing
Sketch the surfaces in Exercises...Ch. 12.6 - Drawing
Sketch the surfaces in Exercises...Ch. 12.6 - Drawing
Sketch the surfaces in Exercises...Ch. 12.6 - Drawing
Sketch the surfaces in Exercises...Ch. 12.6 - Drawing
Sketch the surfaces in Exercises...Ch. 12.6 - Drawing
Sketch the surfaces in Exercises...Ch. 12.6 - Drawing
Sketch the surfaces in Exercises 13–44.
Ch. 12.6 - Drawing
Sketch the surfaces in Exercises...Ch. 12.6 - Drawing
Sketch the surfaces in Exercises...Ch. 12.6 - Drawing
Sketch the surfaces in Exercises...Ch. 12.6 - Drawing
Sketch the surfaces in Exercises 13–44.
Ch. 12.6 - Drawing
Sketch the surfaces in Exercises...Ch. 12.6 - Drawing
Sketch the surfaces in Exercises 13-44.
x2...Ch. 12.6 - Drawing
Sketch the surfaces in Exercises...Ch. 12.6 - Drawing
Sketch the surfaces in Exercises...Ch. 12.6 - Drawing
Sketch the surfaces in Exercises...Ch. 12.6 - Prob. 31ECh. 12.6 - Prob. 32ECh. 12.6 - Prob. 33ECh. 12.6 - Prob. 34ECh. 12.6 - Prob. 35ECh. 12.6 - Prob. 36ECh. 12.6 - Prob. 37ECh. 12.6 - Prob. 38ECh. 12.6 - Prob. 39ECh. 12.6 - Prob. 40ECh. 12.6 - Prob. 41ECh. 12.6 - Prob. 42ECh. 12.6 - Prob. 43ECh. 12.6 - Prob. 44ECh. 12.6 - Express the area A of the cross-section cut from...Ch. 12.6 - Prob. 46ECh. 12.6 - Prob. 47ECh. 12.6 - Prob. 48ECh. 12.6 - Prob. 49ECh. 12.6 - Prob. 50ECh. 12.6 - Prob. 51ECh. 12.6 - Prob. 52ECh. 12 - Prob. 1GYRCh. 12 - Prob. 2GYRCh. 12 - Prob. 3GYRCh. 12 - Prob. 4GYRCh. 12 - Prob. 5GYRCh. 12 - Prob. 6GYRCh. 12 - Prob. 7GYRCh. 12 - Prob. 8GYRCh. 12 - Prob. 9GYRCh. 12 - Prob. 10GYRCh. 12 - Prob. 11GYRCh. 12 - How do you find the distance from a point to a...Ch. 12 - Prob. 13GYRCh. 12 - Prob. 14GYRCh. 12 - Prob. 15GYRCh. 12 - Prob. 16GYRCh. 12 - Prob. 17GYRCh. 12 - Prob. 1PECh. 12 - Prob. 2PECh. 12 - Prob. 3PECh. 12 - Prob. 4PECh. 12 - Prob. 5PECh. 12 - Prob. 6PECh. 12 - Prob. 7PECh. 12 - Prob. 8PECh. 12 - Prob. 9PECh. 12 - Prob. 10PECh. 12 - Prob. 11PECh. 12 - Prob. 12PECh. 12 - Prob. 13PECh. 12 - Prob. 14PECh. 12 - Prob. 15PECh. 12 - Prob. 16PECh. 12 - Prob. 17PECh. 12 - Prob. 18PECh. 12 - Prob. 19PECh. 12 - Prob. 20PECh. 12 - Prob. 21PECh. 12 - Prob. 22PECh. 12 - Prob. 23PECh. 12 - Prob. 24PECh. 12 - Prob. 25PECh. 12 - Prob. 26PECh. 12 - Prob. 27PECh. 12 - Prob. 28PECh. 12 - Prob. 29PECh. 12 - Prob. 30PECh. 12 - Prob. 31PECh. 12 - Prob. 32PECh. 12 - Prob. 33PECh. 12 - Prob. 34PECh. 12 - Prob. 35PECh. 12 - Prob. 36PECh. 12 - Prob. 37PECh. 12 - Prob. 38PECh. 12 - Prob. 39PECh. 12 - Prob. 40PECh. 12 - Prob. 41PECh. 12 - Prob. 42PECh. 12 - Prob. 43PECh. 12 - Prob. 44PECh. 12 - Prob. 45PECh. 12 - Prob. 46PECh. 12 - Prob. 47PECh. 12 - Prob. 48PECh. 12 - Prob. 49PECh. 12 - Prob. 50PECh. 12 - Prob. 51PECh. 12 - Prob. 52PECh. 12 - Prob. 53PECh. 12 - Prob. 54PECh. 12 - Prob. 55PECh. 12 - Prob. 56PECh. 12 - Prob. 57PECh. 12 - Prob. 58PECh. 12 - Prob. 59PECh. 12 - Prob. 60PECh. 12 - Prob. 61PECh. 12 - Prob. 62PECh. 12 - Prob. 63PECh. 12 - Prob. 64PECh. 12 - Prob. 65PECh. 12 - Prob. 66PECh. 12 - Prob. 67PECh. 12 - Prob. 68PECh. 12 - Prob. 69PECh. 12 - Prob. 70PECh. 12 - Prob. 71PECh. 12 - Prob. 72PECh. 12 - Prob. 73PECh. 12 - Prob. 74PECh. 12 - Prob. 75PECh. 12 - Prob. 76PECh. 12 - Prob. 1AAECh. 12 - Prob. 2AAECh. 12 - Prob. 3AAECh. 12 - Prob. 4AAECh. 12 - Prob. 5AAECh. 12 - Prob. 6AAECh. 12 - Prob. 7AAECh. 12 - Prob. 8AAECh. 12 - Prob. 9AAECh. 12 - Prob. 10AAECh. 12 - Prob. 11AAECh. 12 - Prob. 12AAECh. 12 - Prob. 13AAECh. 12 - Prob. 14AAECh. 12 - Prob. 15AAECh. 12 - Prob. 16AAECh. 12 - Prob. 17AAECh. 12 - Prob. 18AAECh. 12 - Prob. 19AAECh. 12 - Prob. 20AAECh. 12 - Prob. 21AAECh. 12 - Prob. 22AAECh. 12 - Prob. 23AAECh. 12 - Prob. 24AAECh. 12 - Prob. 25AAE
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- (a) Use differentiation to find a power series representation for 1 f(x) = (4 + x)²* f(x) = 00 Σ n = 0 What is the radius of convergence, R? R = (b) Use part (a) to find a power series for f(x) = 1 (4 + x)³° f(x) = 00 Σ n = 0 What is the radius of convergence, R? R = (c) Use part (b) to find a power series for f(x) = x² (4 + x)³* 00 f(x) = Σ n = 2 What is the radius of convergence, R? R = Need Help? Read It Watch It SUBMIT ANSWERarrow_forwardanswer for question 4 pleasearrow_forward(3) (20 points) Let F(x, y, z) = (y, z, x²z). Define E = {(x, y, z) | x² + y² ≤ z ≤ 1, x ≤ 0}. (a) (2 points) Calculate the divergence V. F. (b) (4 points) Let D = {(x, y) | x² + y² ≤ 1, x ≤ 0} Without calculation, show that the triple integral √ (V · F) dV = √ 2²(1. = x²(1 − x² - y²) dA. Earrow_forward
- (2) (22 points) Let F(x, y, z) = (x sin y, cos y, ―xy). (a) (2 points) Calculate V. F. (b) (6 points) Given a vector field is everywhere defined with V G₁(x, y, z) = * G2(x, y, z) = − G3(x, y, z) = 0. 0 0 F(x, y, z) = (F₁(x, y, z), F₂(x, y, z), F(x, y, z)) that F = 0, let G = (G1, G2, G3) where F₂(x, y, y, t) dt - √ F³(x, t, 0) dt, * F1(x, y, t) dt, t) dt - √ F Calculate G for the vector field F(x, y, z) = (x sin y, cos y, -xy).arrow_forwardEvaluate the following integral over the Region R. (Answer accurate to 2 decimal places). √ √(x + y) A R R = {(x, y) | 25 < x² + y² ≤ 36, x < 0} Hint: The integral and Region is defined in rectangular coordinates.arrow_forwardFind the volume of the solid that lies under the paraboloid z = 81 - x² - y² and within the cylinder (x − 1)² + y² = 1. A plot of an example of a similar solid is shown below. (Answer accurate to 2 decimal places). Volume using Double Integral Paraboloid & Cylinder -3 Hint: The integral and region is defined in polar coordinates.arrow_forward
- Evaluate the following integral over the Region R. (Answer accurate to 2 decimal places). √4(1–2² 4(1 - x² - y²) dA R 3 R = {(r,0) | 0 ≤ r≤ 2,0π ≤0≤¼˜}. Hint: The integral is defined in rectangular coordinates. The Region is defined in polar coordinates.arrow_forwardEvaluate the following integral over the Region R. (Answer accurate to 2 decimal places). R - 1 · {(r,0) | 1 ≤ r≤ 5,½π≤ 0<1π}. Hint: Be sure to convert to Polar coordinates. Use the correct differential for Polar Coordinates.arrow_forwardEvaluate the following integral over the Region R. (Answer accurate to 2 decimal places). √ √2(x+y) dA R R = {(x, y) | 4 < x² + y² < 25,0 < x} Hint: The integral and Region is defined in rectangular coordinates.arrow_forward
- HW: The frame shown in the figure is pinned at A and C. Use moment distribution method, with and without modifications, to draw NFD, SFD, and BMD. B I I 40 kN/m A 3 m 4 marrow_forwardLet the region R be the area enclosed by the function f(x)= = 3x² and g(x) = 4x. If the region R is the base of a solid such that each cross section perpendicular to the x-axis is an isosceles right triangle with a leg in the region R, find the volume of the solid. You may use a calculator and round to the nearest thousandth. y 11 10 9 00 8 7 9 5 4 3 2 1 -1 -1 x 1 2arrow_forwardLet the region R be the area enclosed by the function f(x) = ex — 1, the horizontal line y = -4 and the vertical lines x = 0 and x = 3. Find the volume of the solid generated when the region R is revolved about the line y = -4. You may use a calculator and round to the nearest thousandth. 20 15 10 5 y I I I | I + -1.5 -1 -0.5 0.5 1 1.5 2 2.5 3 -5 I -10 -15 I + I I T I I + -20 I + -25 I I I -30 I 3.5 4 xarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning

Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
Translations - Primary; Author: corbettmaths;https://www.youtube.com/watch?v=8Dtz5fBe7_Q;License: Standard YouTube License, CC-BY