
Concept explainers
Exercises 9 through 12 refer to a variation of the Koch snowflake called the Koch antisnowflake. The Koch antisnowflake is much like the Koch snowflake, but it is based on a recursive rule that removes equilateral triangles. The recursive replacement rule for the Koch antisnowflake is as follows:
Koch Antisnowflake
• Start: Start with a solid seed equilateral triangle [Fig. 12-36(a) ].
• Replacement rule: In each step replace any boundary line segment ____ with a ![]() (where the point is always facing toward the interior of the snowflake). [Figures 12-36(b) and (c) show the figures obtained at Steps 1 and 2, respectively.
(where the point is always facing toward the interior of the snowflake). [Figures 12-36(b) and (c) show the figures obtained at Steps 1 and 2, respectively.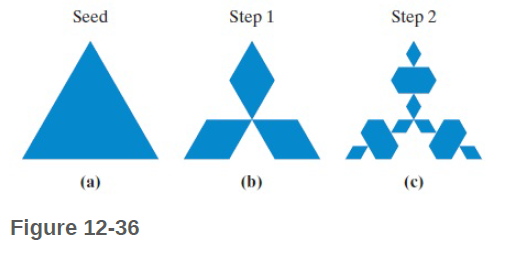
Assume that the seed triangle of the Koch antisnowflake has sides of length
Table
| M | L | P | |
| Start |
|
|
|
| Step
|
|
|
|
| Step
|
|||
| Step
|
|||
| Step
|
|||
| Step
|
Want to see the full answer?
Check out a sample textbook solution
Chapter 12 Solutions
Excursions in Modern Mathematics (9th Edition)
- Q1: A: Let M and N be two subspace of finite dimension linear space X, show that if M = N then dim M = dim N but the converse need not to be true. B: Let A and B two balanced subsets of a linear space X, show that whether An B and AUB are balanced sets or nor. Q2: Answer only two A:Let M be a subset of a linear space X, show that M is a hyperplane of X iff there exists ƒ€ X'/{0} and a € F such that M = (x = x/f&x) = x}. fe B:Show that every two norms on finite dimension linear space are equivalent C: Let f be a linear function from a normed space X in to a normed space Y, show that continuous at x, E X iff for any sequence (x) in X converge to Xo then the sequence (f(x)) converge to (f(x)) in Y. Q3: A:Let M be a closed subspace of a normed space X, constract a linear space X/M as normed space B: Let A be a finite dimension subspace of a Banach space X, show that A is closed. C: Show that every finite dimension normed space is Banach space.arrow_forwardpls helparrow_forwardpls helparrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning  Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL




