
a
To express:
The ratio sin α in terms of a, b, and c.
Answer to Problem 1CT
Solution:
The value of sin α in terms of a, b, and c is sin α =
Explanation of Solution
Definition:
In a right
Given:
The right triangle shown below
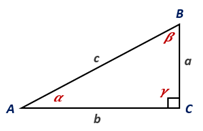
From the figure given,
For the angle α, opposite side = a and hypotenuse = c.
By the definition, sin α =
sin α =
Conclusion:
The value of sin α in terms of a, b, and c is sin α =
b.
To express:
The given tan β in terms of a, b, and c.
Answer to Problem 1CT
Solution:
The value of tan β in terms of a, b, and c is tan β =
Explanation of Solution
Definition:
In a right triangle, the tangent ratio for an acute angle is the ratio
Given:
The right triangle shown below
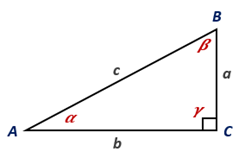
Calculation:
For the angle β, opposite side = b and adjacent side = a.
By the definition, tan β=
tan β =
Conclusion:
The value of tan β in terms of a, b, and c is tan β =
Want to see more full solutions like this?
Chapter 11 Solutions
Elementary Geometry for College Students
- 2arrow_forwardCan someone help me with this please?arrow_forwardMariela is in her classroom and looking out of a window at a tree, which is 20 feet away. Mariela’s line of sight to the top of the tree creates a 42° angle of elevation, and her line of sight to the base of the tree creates a 31° angle of depression. What is the height of the tree, rounded to the nearest foot? Be sure to show your work to explain how you got your answer.arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning  Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,





