Using and Understanding Mathematics: A Quantitative Reasoning Approach (6th Edition)
6th Edition
ISBN: 9780321914620
Author: Jeffrey O. Bennett, William L. Briggs
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 11.B, Problem 17E
Drawing with Perspective. Make the square, circle, and triangle in Figure 11.32 into three-dimensional solid objects: a box, a cylinder, and a triangular prism, respectively. The given objects should be used as the front faces of the three-dimensional objects, and all figures should be drawn with correct perspective relative to the given vanishing point P.
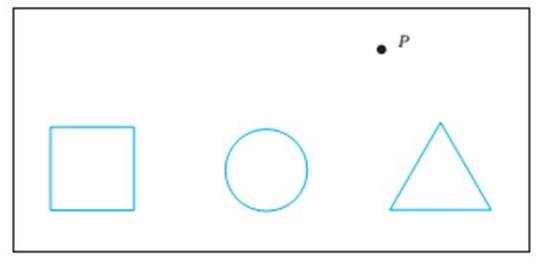
FIGURE 11.32
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Refer to page 312 for a set of mappings between two groups G and H.
Instructions:
•
•
Verify which of the provided mappings are homomorphisms.
Determine the kernel and image of valid homomorphisms and discuss their properties.
•
State whether the groups are isomorphic, justifying your conclusion.
Link: [https://drive.google.com/file/d/1wKSrun-GlxirS3IZ9qo Hazb9tC440 AZF/view?usp=sharing]
12:25 AM Sun Dec 22
uestion 6- Week 8: QuX
Assume that a company X +
→ C
ezto.mheducation.com
Week 8: Quiz i
Saved
6
4
points
Help
Save & Exit
Submit
Assume that a company is considering purchasing a machine for $50,000 that will have a five-year useful life and a $5,000 salvage value. The
machine will lower operating costs by $17,000 per year. The company's required rate of return is 15%. The net present value of this investment
is closest to:
Click here to view Exhibit 12B-1 and Exhibit 12B-2, to determine the appropriate discount factor(s) using the tables provided.
00:33:45
Multiple Choice
О
$6,984.
$11,859.
$22,919.
○ $9,469,
Mc
Graw
Hill
2
100-
No chatgpt pls will upvote
Chapter 11 Solutions
Using and Understanding Mathematics: A Quantitative Reasoning Approach (6th Edition)
Ch. 11.A - Prob. 1QQCh. 11.A - Prob. 2QQCh. 11.A - Prob. 3QQCh. 11.A - Prob. 4QQCh. 11.A - Prob. 5QQCh. 11.A - Prob. 6QQCh. 11.A - Prob. 7QQCh. 11.A - Prob. 8QQCh. 11.A - Prob. 9QQCh. 11.A - Prob. 10QQ
Ch. 11.A - Prob. 1ECh. 11.A - 2. Define fundamental frequency, harmonic, and...Ch. 11.A - 3. What is a 12-tone scale? How are the...Ch. 11.A - 4. Explain how the notes of the scale are...Ch. 11.A - Prob. 5ECh. 11.A - Prob. 6ECh. 11.A - Prob. 7ECh. 11.A - Prob. 8ECh. 11.A - Prob. 9ECh. 11.A - Prob. 10ECh. 11.A - Prob. 11ECh. 11.A - Prob. 12ECh. 11.A - Octaves. Starting with a tone having a frequency...Ch. 11.A - Notes of a Scale. Find the frequencies of the 12...Ch. 11.A - Prob. 15ECh. 11.A - 16. The Dilemma of Temperament. Start at middle A,...Ch. 11.A - Exponential Growth and Scales. Starting at middle...Ch. 11.A - 18. Exponential Growth and Scales. Starting at...Ch. 11.A - 19. Exponential Decay and Scales. What is the...Ch. 11.A - Prob. 20ECh. 11.A - Prob. 21ECh. 11.A - Prob. 22ECh. 11.A - Mathematics and Music. Visit a website devoted to...Ch. 11.A - Mathematics and Composers. Many musical composers,...Ch. 11.A - Prob. 25ECh. 11.A - Prob. 26ECh. 11.A - Digital Processing. A variety of apps and software...Ch. 11.A - Prob. 28ECh. 11.B - Prob. 1QQCh. 11.B - 2. All lines that are parallel in a real scene...Ch. 11.B - 3. The Last Supper in Figure 11.6. Which of the...Ch. 11.B - Prob. 4QQCh. 11.B - Prob. 5QQCh. 11.B - Prob. 6QQCh. 11.B - Prob. 7QQCh. 11.B - Prob. 8QQCh. 11.B - Prob. 9QQCh. 11.B - Prob. 10QQCh. 11.B - Prob. 1ECh. 11.B - Prob. 2ECh. 11.B - Prob. 3ECh. 11.B - Prob. 4ECh. 11.B - Prob. 5ECh. 11.B - 6. Briefly explain why there are only three...Ch. 11.B - 7. Briefly explain why more tilings are possible...Ch. 11.B - 8. What is the difference between periodic and...Ch. 11.B - Prob. 9ECh. 11.B - Prob. 10ECh. 11.B - Prob. 11ECh. 11.B - Prob. 12ECh. 11.B - Prob. 13ECh. 11.B - Prob. 14ECh. 11.B - Vanishing Points. Consider the simple drawing of a...Ch. 11.B - Correct Perspective. Consider the two boxes shown...Ch. 11.B - Drawing with Perspective. Make the square, circle,...Ch. 11.B - Drawing MATH with Perspective. Make the letters M,...Ch. 11.B - 19. The drawing in Figure 11.34 shows two poles...Ch. 11.B - Two Vanishing Points. Figure 11.35 shows a road...Ch. 11.B - Prob. 21ECh. 11.B - Prob. 22ECh. 11.B - Prob. 23ECh. 11.B - Prob. 24ECh. 11.B - Prob. 25ECh. 11.B - Prob. 26ECh. 11.B - Prob. 27ECh. 11.B - Prob. 28ECh. 11.B - Prob. 29ECh. 11.B - Prob. 30ECh. 11.B - 30-31 : Tilings from Translating and Reflecting...Ch. 11.B - 32-33: Tilings from Quadrilaterals. Make a tiling...Ch. 11.B - Tilings from Quadrilaterals. Make a tiling from...Ch. 11.B - Prob. 34ECh. 11.B - Prob. 35ECh. 11.B - Prob. 36ECh. 11.B - Prob. 37ECh. 11.B - Prob. 38ECh. 11.B - Art and Mathematics. Visit a website devoted to...Ch. 11.B - 40. Art Museums. Choose an art museum, and study...Ch. 11.B - Prob. 41ECh. 11.B - Penrose Tilings. Learn more about the nature and...Ch. 11.B - Prob. 43ECh. 11.C - Prob. 1QQCh. 11.C - 2. Which of the following is not a characteristic...Ch. 11.C - 3. If a 1-foot line segment is divided according...Ch. 11.C - 4. To make a golden rectangle, you should
a. a...Ch. 11.C - Prob. 5QQCh. 11.C - Prob. 6QQCh. 11.C - Suppose you start with a golden rectangle and cut...Ch. 11.C - Prob. 8QQCh. 11.C - Prob. 9QQCh. 11.C - Prob. 10QQCh. 11.C - Prob. 1ECh. 11.C - How is a golden rectangle formed?Ch. 11.C - What evidence suggests that the golden ratio and...Ch. 11.C - Prob. 4ECh. 11.C - 5. What is the Fibonacci sequence?
Ch. 11.C - 6. What is the connection between the Fibonacci...Ch. 11.C - 7. Maria cut her 4-foot walking stick into two...Ch. 11.C - Prob. 8ECh. 11.C - Prob. 9ECh. 11.C - Prob. 10ECh. 11.C - Prob. 11ECh. 11.C - Prob. 12ECh. 11.C - Prob. 13ECh. 11.C - Prob. 14ECh. 11.C - Prob. 15ECh. 11.C - Prob. 16ECh. 11.C - Prob. 17ECh. 11.C - 18. Everyday Golden Rectangles. Find at least...Ch. 11.C - 19. Finding . The property that defines the golden...Ch. 11.C - 20. Properties of
a. Enter into your calculator....Ch. 11.C - Prob. 21ECh. 11.C - The Lucas Sequence. A sequence called the Lucas...Ch. 11.C - Prob. 23ECh. 11.C - The Golden Navel. An Old theory claims that, on...Ch. 11.C - Prob. 25ECh. 11.C - Prob. 26ECh. 11.C - Prob. 27ECh. 11.C - Prob. 28ECh. 11.C - Golden Controversies. Many websites are devoted to...Ch. 11.C - 30. Fibonacci Numbers. Learn more about Fibonacci...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- 7. [10 marks] Let G = (V,E) be a 3-connected graph. We prove that for every x, y, z Є V, there is a cycle in G on which x, y, and z all lie. (a) First prove that there are two internally disjoint xy-paths Po and P₁. (b) If z is on either Po or P₁, then combining Po and P₁ produces a cycle on which x, y, and z all lie. So assume that z is not on Po and not on P₁. Now prove that there are three paths Qo, Q1, and Q2 such that: ⚫each Qi starts at z; • each Qi ends at a vertex w; that is on Po or on P₁, where wo, w₁, and w₂ are distinct; the paths Qo, Q1, Q2 are disjoint from each other (except at the start vertex 2) and are disjoint from the paths Po and P₁ (except at the end vertices wo, W1, and w₂). (c) Use paths Po, P₁, Qo, Q1, and Q2 to prove that there is a cycle on which x, y, and z all lie. (To do this, notice that two of the w; must be on the same Pj.)arrow_forward6. [10 marks] Let T be a tree with n ≥ 2 vertices and leaves. Let BL(T) denote the block graph of T. (a) How many vertices does BL(T) have? (b) How many edges does BL(T) have? Prove that your answers are correct.arrow_forward4. [10 marks] Find both a matching of maximum size and a vertex cover of minimum size in the following bipartite graph. Prove that your answer is correct. ย ພarrow_forward
- 5. [10 marks] Let G = (V,E) be a graph, and let X C V be a set of vertices. Prove that if |S||N(S)\X for every SCX, then G contains a matching M that matches every vertex of X (i.e., such that every x X is an end of an edge in M).arrow_forwardQ/show that 2" +4 has a removable discontinuity at Z=2i Z(≥2-21)arrow_forwardRefer to page 100 for problems on graph theory and linear algebra. Instructions: • Analyze the adjacency matrix of a given graph to find its eigenvalues and eigenvectors. • Interpret the eigenvalues in the context of graph properties like connectivity or clustering. Discuss applications of spectral graph theory in network analysis. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS3IZ9qoHazb9tC440 AZF/view?usp=sharing]arrow_forward
- Refer to page 110 for problems on optimization. Instructions: Given a loss function, analyze its critical points to identify minima and maxima. • Discuss the role of gradient descent in finding the optimal solution. . Compare convex and non-convex functions and their implications for optimization. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qo Hazb9tC440 AZF/view?usp=sharing]arrow_forwardRefer to page 140 for problems on infinite sets. Instructions: • Compare the cardinalities of given sets and classify them as finite, countable, or uncountable. • Prove or disprove the equivalence of two sets using bijections. • Discuss the implications of Cantor's theorem on real-world computation. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qoHazb9tC440 AZF/view?usp=sharing]arrow_forwardRefer to page 120 for problems on numerical computation. Instructions: • Analyze the sources of error in a given numerical method (e.g., round-off, truncation). • Compute the error bounds for approximating the solution of an equation. • Discuss strategies to minimize error in iterative methods like Newton-Raphson. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qo Hazb9tC440 AZF/view?usp=sharing]arrow_forward
- Refer to page 145 for problems on constrained optimization. Instructions: • Solve an optimization problem with constraints using the method of Lagrange multipliers. • • Interpret the significance of the Lagrange multipliers in the given context. Discuss the applications of this method in machine learning or operations research. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qo Hazb9tC440 AZF/view?usp=sharing]arrow_forwardOnly 100% sure experts solve it correct complete solutions okarrow_forwardGive an example of a graph with at least 3 vertices that has exactly 2 automorphisms(one of which is necessarily the identity automorphism). Prove that your example iscorrect.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:9781305658004
Author:Ron Larson
Publisher:Cengage Learning
College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
What is Ellipse?; Author: Don't Memorise;https://www.youtube.com/watch?v=nzwCInIMlU4;License: Standard YouTube License, CC-BY