
Concept explainers
a.
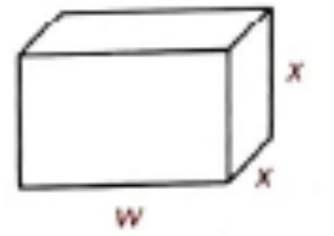
The equation of a ration function that gives the surface area of the lunch box in terms of x .
a.
Answer to Problem 1MP
Explanation of Solution
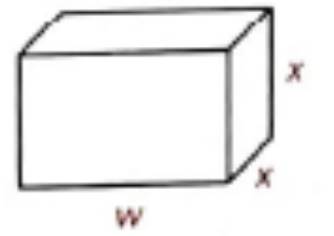
Given:
The volume of the lunch box is,
Concept Used:
- Least Common Denominator (LCD) is the smallest number that is divisible by the denominator of all the fractions that are being added or subtracted.
- Solving an equation containing rational expressions
- Multiply both sides of equations by LCD(least common denominator) of all denominators.
- Remove any grouping symbols and solve the resulting equation for the variable asked in equation
Calculation:
The expression for the surface area of the lunch box is given by,
So, in the expression of surface area, the first term has no denominator, so it can be considered 1 as its denominator. The denominator of second term is x , so the least common denominator of 1 and x should be x . So, multiply the first term by x up and down and then simplify the numerators over the common denominator as shown below,
Thus, the equation of a rational expression for the surface area of lunch box is
b.
The graph of the function for
b.
Explanation of Solution
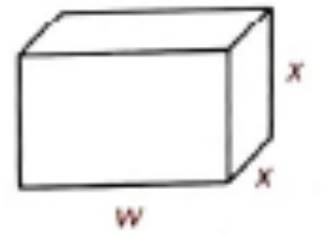
Given:
The volume of the lunch box is,
Concept Used:
- Least Common Denominator (LCD) is the smallest number that is divisible by the denominator of all the fractions that are being added or subtracted.
- Solving an equation containing rational expressions
- Multiply both sides of equations by LCD(least common denominator) of all denominators.
- Remove any grouping symbols and solve the resulting equation for the variable asked in equation
Calculation:
The graph of the surface area function is shown below,
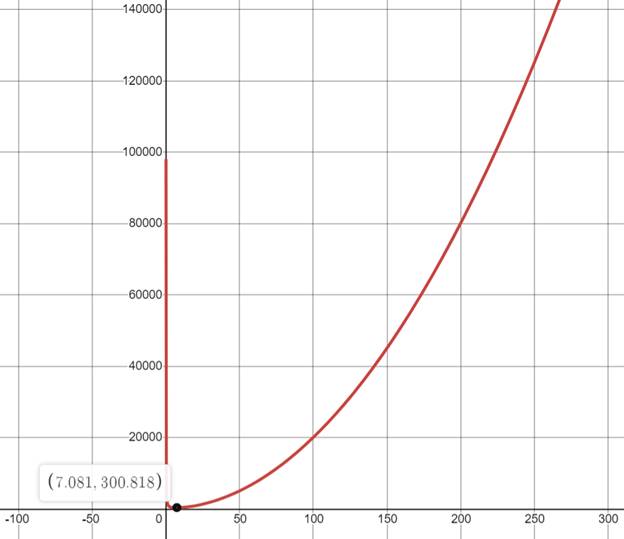
The graph represents the amount of cardboard needed S(x) on vertical axis, for the side length x of the box in horizontal axis.
c.
The coordinate of the minimum point of the function.
c.
Answer to Problem 1MP
Explanation of Solution
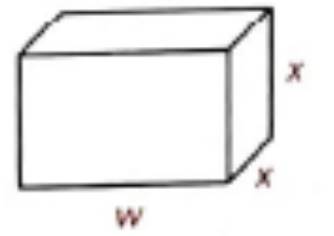
Given:
The volume of the lunch box is,
Concept Used:
- Least Common Denominator (LCD) is the smallest number that is divisible by the denominator of all the fractions that are being added or subtracted.
- Solving an equation containing rational expressions
- Multiply both sides of equations by LCD(least common denominator) of all denominators.
- Remove any grouping symbols and solve the resulting equation for the variable asked in equation
Calculation:
The graph of the surface area function is shown below,
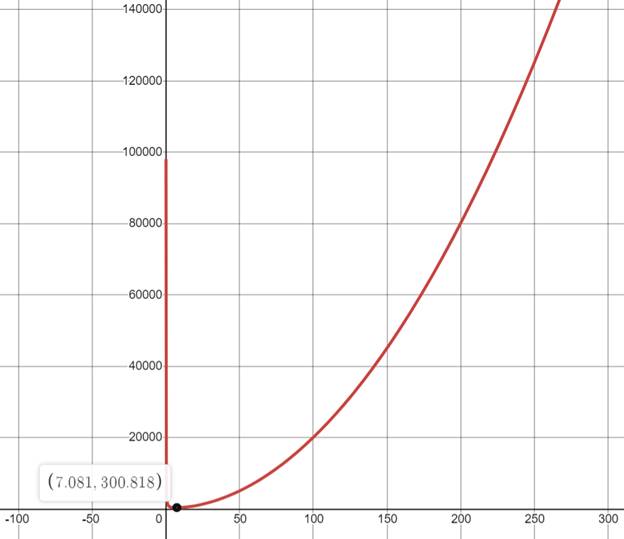
The graph represents the amount of cardboard needed S(x) on vertical axis, for the side length x of the box in horizontal axis.
From the graph it is clear the coordinates of the minimum point rounded to nearest hundredth is
d.
What does the minimum point tell.
d.
Explanation of Solution
Given:
The volume of the lunch box is,
Calculation:
The minimum point of the graph tells that when the length of the base of the box is
Chapter 11 Solutions
High School Math 2011 Algebra 1 Student Companion Grade 8/9
Additional Math Textbook Solutions
College Algebra (7th Edition)
Elementary Statistics (13th Edition)
Thinking Mathematically (6th Edition)
Intro Stats, Books a la Carte Edition (5th Edition)
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Pre-Algebra Student Edition
- 5. Consider the following vectors 0.1 3.2 -0-0-0 = 5.4 6.0 = z= 3 0.1 For each of exercises a-e, either compute the desired quantity by hand with work shown or explain why the desired quantity is not defined. (a) 10x (b) 10-27 (c) J+Z (d) (x, y) (e) (x, z)arrow_forwardConsider the graph/network plotted below. 1 6 5 3 Explicitly give (i.e., write down all of the entries) the adjacency matrix A of the graph.arrow_forward. Given the function f: XY (with X and Y as above) defined as f(2) = 2, f(4) = 1, ƒ(6)=3, ƒ(8) = 2, answer the following questions. Justify your answers. (a) [4 points] Is f injective? (b) [4 points] Is f surjective? (c) [2 points] Is f bijective?arrow_forward
- 1. Let 15 -14 A = -10 9 13-12 -8 7 11 15 -14 13 -12 -6 and B = -10 9 -8 7 -6 5 -4 3 -2 E 5 -4 3 -2 1 Explicitly give the values of A2,3, A1,5, and B1,4- Is A a 5 x 3 matrix? Explain your answer. Are A and B (mathematically) equal? Explain your answer.arrow_forwardGiven the following set X = {2, 4, 6, 8} and Y = {1, 2, 3}, explicitly give (e.g., write down the sets with numerical entries) of the outputs of the following requested set operations: (a) [2 points] XUY (Union) (b) [2 points] XY (Intersection) (c) [3 points] X\Y (Difference) (d) [3 points] XAY (Symmetric Difference)arrow_forwardFor what values of k will the equation (k + 1)x² + 6kx + 2k² - x = 0 have: a) one root equal zero b) one root the reciprocal of the other c) roots numerically equal but of opposite signarrow_forward
- 1) Find The inverse The domain of m(x) = tion and of the function The inverse function 3- √x-aarrow_forwardGraph the following function. Please also graph the asymptote. Thank you.arrow_forwardFile Edit View History Bookmarks Profiles Tab Window Window Help Things Quadratics! Part 1 X SM◄))) 61% Fri 25 student.desmos.com/activitybuilder/instance/67b739e7356cae7898fd0dbd/student/67b8f115811d42186c239e23#screenid=41a95 ngs Quadratics! Part 1: Parabolas Mitchell 30 30 foo feet 20- 20 10 0 -10 FEB 21 3 10 10 80 FS F3 X Intercepts #2 20 20 Approximately how tall is the shooter? > Which intercept did you use to solve the above problem? x-intercept y-intercept 30 feet Explain your thinking. 1 √E Submit 00000 acBook stv 399 ? DOD 000 F4 % 5 W E R F5 A F6 F7 F9 & * 7 8 9 0 Y U C 014arrow_forward
- The table below shows the acreage, number of visitors, and total revenue of state parks and recreational areas in Massachusetts, New York, and Vermont in 2010. State Acreage (in thousands) Visitors (in thousands) Revenue (in thousands) Massachusetts 350 35,271 $12,644 New York 1,354 56,322 $85,558 Vermont 69 758 $10,969 Select the three true statements based on the data in the table. A. Vermont had the highest revenue per acre of state parks and recreational areas. B. Vermont had approximately 11 visitors per acre of state parks and recreational areas. C. New York had the highest number of visitors per acre of state parks and recreational areas. D. Massachusetts had approximately 36 visitors per acre of state parks and recreational areas. E. New York had revenue of approximately $63.19 per acre of state parks and recreational areas. F. Massachusetts had revenue of approximately $0.03 per acre of state parks and recreational areas.arrow_forwarda) show that the empty set and sigletonset are convex set. 6) show that every sub space of linear space X is convex but the convers heed not be true. c) let Mand N be two convex set of a linear Space X and KEF Show that MUN is conevex and (ii) M-N is convex or hot A and is MSN or NSM show that MUN convex or not, 385arrow_forwardI write with prove one-to-one linear Sanction but not onto Lexample.) b) write with Prove on to linear function but not oh-to-on (example). c) write with prove example x=y St Xandy two linear space over Sielad F.arrow_forward
 Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education





