Chapter 11.3, Problem 37E

To determine

Perform ANOVA to test the significance at 1% level of significance.

Answer to Problem 37E

The ANOVA for the given data is shown below:

Source	Degrees of freedom	Sum of squares	Mean sum of squares	F-ratio
Fabric A	2	4,414.658	2207.329	2259.293
Type of exposure B	1	47.255	47.255	48.36745
Degree of exposure C	2	983.566	491.783	503.3603
Fabric direction D	1	0.044	0.044	0.045036
Interaction AB	2	30.606	15.303	15.66325
Interaction AC	2	1,101.754	275.446	281.9304
Interaction AD	2	0.94	0.47	0.481064
Interaction BC	2	4.282	2.141	2.191402
Interaction BD	1	0.273	0.273	0.279427
Interaction CD	2	0.494	0.247	0.252815
Interaction ABC	4	14.856	3.714	3.801433
Interaction ABD	2	8.144	4.072	4.167861
Interaction ACD	4	3.068	0.767	0.785056
Interaction BCD	2	0.56	0.28	0.286592
Interaction ABCD	4	1.389	0.347	0.355
Error	36	35.172	0.977
Total	71	6,647.091	9.621

There is sufficient of evidence to conclude that there is an effect of fabric on the extent of color change at 1% level of significance.

There is sufficient of evidence to conclude that there is an effect exposure type on the extent of color change at 1% level of significance.

There is sufficient of evidence to conclude that there is an effect of exposure level on the extent of color change at 1% level of significance.

There is no sufficient of evidence to conclude that there is an effect of fabric direction on the extent of color change at 1% level of significance.

There is sufficient of evidence to conclude that there is an interaction effect of fabric and exposure type on the extent of color change at 1% level of significance.

There is sufficient of evidence to conclude that there is an interaction effect of fabric and exposure level on the extent of color change at 1% level of significance.

There is no sufficient of evidence to conclude that there is an interaction effect of fabric and fabric direction on the extent of color change at 1% level of significance.

There is no sufficient of evidence to conclude that there is an interaction effect of exposure type and exposure level on the extent of color change at 1% level of significance.

There is no sufficient of evidence to conclude that there is an interaction effect of exposure type and fabric direction on the extent of color change at 1% level of significance.

There is no sufficient of evidence to conclude that there is an interaction effect of exposure level and fabric direction on the extent of color change at 1% level of significance.

There is no sufficient of evidence to conclude that there is an interaction effect of fabric, exposure type and exposure level on the extent of color change at 1% level of significance.

There is no sufficient of evidence to conclude that there is an interaction effect of fabric, exposure type and fabric direction on the extent of color change at 1% level of significance.

There is no sufficient of evidence to conclude that there is an interaction effect of fabric, exposure level and fabric direction on the extent of color change at 1% level of significance.

There is no sufficient of evidence to conclude that there is an interaction effect of exposure type, exposure level and fabric direction on the extent of color change at 1% level of significance.

There is no sufficient of evidence to conclude that there is an interaction effect of fabric, exposure type, exposure level and fabric direction on the extent of color change at 1% level of significance.

Explanation of Solution

Given info:

An experiment was conducted to test the effect of fabric, type of exposure, level of exposure and fabric direction on the color change of the fabric. Two observation were noted for each of the four factors.

Calculation:

The general ANOVA table is given below:

Source	Degrees of freedom	Sum of squares	Mean sum of squares	F-ratio
Factor A	$I-1$	$\text{SSA}={{\displaystyle \sum _i^{}{\displaystyle \sum _j^{}{\displaystyle \sum _k{\displaystyle \sum _p^{}\left({\overline{X}}_{i\cdot \cdot \cdot }-\overline{X_{\cdot \cdot \cdot \cdot }}\right)}}}}}^2$	$\text{MSA}=\frac{\text{SSA}}{\left(I-1\right)}$	$f_A=\frac{\text{MSA}}{\text{MSE}}$
Factor B	$J-1$	$\text{SSB}={{\displaystyle \sum _i^{}{\displaystyle \sum _j^{}{\displaystyle \sum _k{\displaystyle \sum _p^{}\left({\overline{X}}_{\cdot j\cdot \cdot }-\overline{X_{\cdot \cdot \cdot \cdot }}\right)}}}}}^2$	$\text{MSB}=\frac{\text{SSB}}{\left(J-1\right)}$	$f_B=\frac{\text{MSB}}{\text{MSE}}$
Factor C	$K-1$	$\text{SSC}={{\displaystyle \sum _i^{}{\displaystyle \sum _j^{}{\displaystyle \sum _k{\displaystyle \sum _p^{}\left({\overline{X}}_{\cdot \cdot k\cdot }-\overline{X_{\cdot \cdot \cdot \cdot }}\right)}}}}}^2$	$\text{MSC}=\frac{\text{SSC}}{\left(K-1\right)}$	$f_C=\frac{\text{MSC}}{\text{MSE}}$
Factor D	$P-1$	$\text{SSD}={{\displaystyle \sum _i^{}{\displaystyle \sum _j^{}{\displaystyle \sum _k{\displaystyle \sum _p^{}\left({\overline{X}}_{\cdot \cdot \cdot P}-\overline{X_{\cdot \cdot \cdot \cdot }}\right)}}}}}^2$	$\text{MSD}=\frac{\text{SSC}}{\left(P-1\right)}$	$f_C=\frac{\text{MSC}}{\text{MSE}}$
Interaction AB	$\left(I-1\right)\left(J-1\right)$	$\begin{array}{l}\text{SSAB}\\ =KPL{{\displaystyle \sum _i^{}{\displaystyle \sum _j^{}\left({\overline{X}}_{ij\cdot \cdot }-{\overline{X}}_{i\cdot \cdot \cdot }-{\overline{X}}_{\cdot j\cdot \cdot }-{\overline{X}}_{\cdot \cdot \cdot p}+\overline{X_{\cdot \cdot \cdot \cdot }}\right)}}}^2\end{array}$	$\text{MSAB}=\frac{\text{SSAB}}{\left(I-1\right)\left(J-1\right)}$	$f_{AB}=\frac{\text{MSAB}}{\text{MSE}}$
Interaction ABC	$\left(I-1\right)\left(J-1\right)\left(K-1\right)$	$\begin{array}{l}\text{SSABC}\\ =L{{\displaystyle \sum _i^{}{\displaystyle \sum _j{\displaystyle \sum _k^{}\left(\begin{array}{l}{\overline{X}}_{ijk\cdot }-{\overline{X}}_{ij\cdot \cdot }-{\overline{X}}_{i\cdot k\cdot }-{\overline{X}}_{\cdot jk\cdot }+\\ {\overline{X}}_{i\cdot \cdot \cdot }+{\overline{X}}_{\cdot j\cdot \cdot }+{\overline{X}}_{\cdot \cdot k\cdot }-{\overline{X}}_{\cdot \cdot \cdot \cdot }\end{array}\right)}}}}^2\end{array}$	$\begin{array}{l}\text{MSABC}\\ =\frac{\text{SSABC}}{\left(I-1\right)\left(J-1\right)\left(K-1\right)}\end{array}$	$f_{ABC}=\frac{\text{MSABC}}{\text{MSE}}$
Error	$IJPK\left(L-1\right)$	$\text{SSE}={{\displaystyle \sum _i^{}{\displaystyle \sum _j^{}{\displaystyle \sum _k{\displaystyle \sum _p{\displaystyle \sum _l^{}\left(X_{ijkpl}-{\overline{X}}_{ijkp\cdot }\right)}}}}}}^2$	$\text{MSE}=\frac{\text{SSE}}{IJK\left(L-1\right)}$
Total	$IJKPL-1$	$\text{SST}={{\displaystyle \sum _i^{}{\displaystyle \sum _j^{}{\displaystyle \sum _k{\displaystyle \sum _p{\displaystyle \sum _l^{}\left(X_{ijkpl}-{\overline{X}}_{\cdot \cdot \cdot \cdot \cdot }\right)}}}}}}^2$

The sum of squares for each factor and interaction is calculated by multiplying the mean sum of squares with its corresponding degrees of freedom.

Sum of squares excluding ABCD:

Source	Sum of squares
A	4,414.658
B	47.255
C	983.566
D	0.044
AB	30.606
AC	1,101.784
AD	0.94
BC	4.282
BD	0.273
CD	0.494
ABC	14.856
ABD	8.144
ACD	3.068
BCD	0.56
Error	35.172
Total	6,647.091

Using the above table SSABCD can be calculated:

$\begin{array}{c}SST=\left[\begin{array}{l}SSA+SB+SSC+SSD+SSAB+SSAC+SSAD+SSBC+\\ SSCD+SSABC+SSABD+SSACD+SSBCD+SSABCD\end{array}\right]\\ SSABCD=SST-\left[\begin{array}{l}SSA+SB+SSC+SSD+SSAB+SSAC+SSAD+SSBC+\\ SSCD+SSABC+SSABD+SSACD+SSBCD+SSABCD\end{array}\right]\\ =6,647.091-\left[\begin{array}{l}4,414.658+47.255+983.566+0.044+30.606+\\ 1,101.784+0.94+4.282+0.273+0.494+14.856+\\ 8.144+3.068+0.56+35.172\end{array}\right]\\ =6,647.091-6,645.702\end{array}$

$=1.389$

The mean sum of squares for the interaction ABCD is given below:

$\begin{array}{c}MSABCD=\frac{SSABCD}{\left(I-1\right)\left(J-1\right)\left(K-1\right)\left(P-1\right)}\\ =\frac{1.389}{\left(3-1\right)\left(2-1\right)\left(3-1\right)\left(2-1\right)}\\ =\frac{1.389}{\left(2\right)\left(1\right)\left(2\right)\left(1\right)}\\ =\frac{1.389}{4}\end{array}$

                 $=0.347$

Thus, the mean sum of squares for the interaction ABCD is 0.347.

The ANOVA for the given data is shown below:

Source	Degrees of freedom	Sum of squares	Mean sum of squares	F-ratio
Fabric A	$3-1=2$	4,414.658	2207.329	2,259.293
Type of exposure B	$2-1=1$	47.255	47.255	48.36745
Degree of exposure C	$3-1=2$	983.566	491.783	503.3603
Fabric direction D	$2-1=1$	0.044	0.044	0.045036
Interaction AB	$\left(3-1\right)\left(2-1\right)=2$	30.606	15.303	15.66325
Interaction AC	$\left(2-1\right)\left(3-1\right)=2$	1,101.754	275.446	281.9304
Interaction AD	$\left(3-1\right)\left(2-1\right)=2$	0.94	0.47	0.481064
Interaction BC	$\left(2-1\right)\left(3-1\right)=2$	4.282	2.141	2.191402
Interaction BD	$\left(2-1\right)\left(2-1\right)=1$	0.273	0.273	0.279427
Interaction CD	$\left(3-1\right)\left(2-1\right)=2$	0.494	0.247	0.252815
Interaction ABC	$\left(3-1\right)\left(2-1\right)\left(3-1\right)=4$	14.856	3.714	3.801433
Interaction ABD	$\left(3-1\right)\left(2-1\right)\left(2-1\right)=2$	8.144	4.072	4.167861
Interaction ACD	$\left(3-1\right)\left(3-1\right)\left(2-1\right)=4$	3.068	0.767	0.785056
Interaction BCD	$\left(2-1\right)\left(3-1\right)\left(2-1\right)=2$	0.56	0.28	0.286592
Interaction ABCD	$\left(3-1\right)\left(2-1\right)\left(3-1\right)\left(2-1\right)=4$	1.389	0.347	0.355
Error	$\begin{array}{c}3\times 2\times 3\times 2\left(2-1\right)=36\left(1\right)\\ =36\end{array}$	35.172	0.977
Total	$\begin{array}{c}3\times 2\times 3\times 2\times 2-1=72-1\\ =71\end{array}$	6,647.091	9.621

Where,

The F statistic for each factor is obtained by dividing the mean sum of squares with the mean sum of squares due to error.

Testing the main effects:

Testing the Hypothesis for the factor A:

Null hypothesis:

$H_0{}_A:{\alpha }_1={\alpha }_2={\alpha }_3=0$

That is, there is no significant difference in the extent of color change due to the three levels of fabrics.

Alternative hypothesis:

$H_{aA}:\text{At least one of the }{\alpha }_i\text{'}s\ne 0$

That is, there is significant difference in the extent of color change due to the three levels of fabrics.

Testing the Hypothesis for the factor B:

Null hypothesis:

$H_0{}_B:{\beta }_1={\beta }_2={\beta }_3=0$

That is, there is no significant difference in the extent of color change due to the two levels of exposure type.

Alternative hypothesis:

$H_{aB}:\text{At least one of the }{\beta }_j\text{'}s\ne 0$

That is, there is a significant difference in the extent of color change due to the two levels of exposure type.

Testing the Hypothesis for the factor C:

Null hypothesis:

$H_0{}_C:{\delta }_1={\delta }_2={\delta }_3=0$

That is, there is no significant difference in the extent of color change due to the three levels of exposure level.

Alternative hypothesis:

$H_{aC}:\text{At least one of the }{\delta }_k\text{'}s\ne 0$

That is, there is a significant difference in the extent of color change due to the three levels of exposure level.

Testing the Hypothesis for the factor D:

Null hypothesis:

$H_0{}_D:{\lambda }_1={\lambda }_2=0$

That is, there is no significant difference in the extent of color change due to the two levels of fabric direction.

Alternative hypothesis:

$H_{aD}:\text{At least one of the }{\lambda }_p\text{'}s\ne 0$

That is, there is a significant difference in the extent of color change due to the two levels of fabric direction.

Testing the Hypothesis for the interaction effect of AB:

Null hypothesis:

$H_0{}_{AB}:{\gamma }_{ij}{}^{AB}\text{'}\text{s}=0$

That is, there is no significant difference in the extent of color change due to the interaction between fabric and exposure type.

Alternative hypothesis:

$H_a{}_{AB}:\text{At least one of }{\gamma }_{ij}{}^{AB}\text{'}\text{s}\ne 0$

That is, there is significant difference in the extent of color change due to the interaction between fabric and exposure type.

Testing the Hypothesis for the interaction effect AC:

Null hypothesis:

$H_0{}_{AC}:{\gamma }_{ij}{}^{AC}\text{'}\text{s}=0$

That is, there is no significant difference in the extent of color change due to the interaction between fabric and exposure level.

Alternative hypothesis:

$H_a{}_{AC}:\text{At least one of }{\gamma }_{ij}{}^{AC}\text{'}\text{s}\ne 0$

That is, there is a significant difference in the extent of color change due to the interaction between fabric and exposure level.

Testing the Hypothesis for the interaction effect AD:

Null hypothesis:

$H_0{}_{AD}:{\gamma }_{ij}{}^{AD}\text{'}\text{s}=0$

That is, there is no significant difference in the extent of color change due to the interaction between fabric and fabric direction.

Alternative hypothesis:

$H_a{}_{AD}:\text{At least one of }{\gamma }_{ij}{}^{AD}\text{'}\text{s}\ne 0$

That is, there is a significant difference in the extent of color change due to the interaction between fabric and fabric direction.

Testing the Hypothesis for the interaction effect BC:

Null hypothesis:

$H_0{}_{BC}:{\gamma }_{ij}{}^{BC}\text{'}\text{s}=0$

That is, there is no significant difference in the extent of color change due to the interaction between exposure type and exposure level.

Alternative hypothesis:

$H_a{}_{BC}:\text{At least one of }{\gamma }_{ij}{}^{BC}\text{'}\text{s}\ne 0$

That is, there is significant difference in the extent of color change due to the interaction between exposure type and exposure level.

Testing the Hypothesis for the interaction effect BD:

Null hypothesis:

$H_0{}_{BD}:{\gamma }_{ij}{}^{BD}\text{'}\text{s}=0$

That is, there is no significant difference in the extent of color change due to the interaction between exposure type and fabric direction.

Alternative hypothesis:

$H_a{}_{BD}:\text{At least one of }{\gamma }_{ij}{}^{BD}\text{'}\text{s}\ne 0$

That is, there is significant difference in the extent of color change due to the interaction between exposure type and fabric direction.

Testing the Hypothesis for the interaction effect CD:

Null hypothesis:

$H_0{}_{CD}:{\gamma }_{ij}{}^{CD}\text{'}\text{s}=0$

That is, there is no significant difference in the extent of color change due to the interaction between exposure level and fabric direction.

Alternative hypothesis:

$H_a{}_{CD}:\text{At least one of }{\gamma }_{ij}{}^{CD}\text{'}\text{s}\ne 0$

That is, there is significant difference in the extent of color change due to the interaction between exposure level and fabric direction.

Testing the Hypothesis for the interaction effect ABC:

Null hypothesis:

$H_0{}_{ABC}:{\gamma }_{ijk}{}^{ABC}\text{'}\text{s}=0$

That is, there is no significant difference in the extent of color change due to the interaction between fabric, exposure type and exposure level.

Alternative hypothesis:

$H_a{}_{ABC}:\text{At least one of }{\gamma }_{ijk}{}^{ABC}\text{'}\text{s}\ne 0$

That is, there is a significant difference in the extent of color change due to the interaction between fabric, exposure type and exposure level.

Testing the Hypothesis for the interaction effect ABD:

Null hypothesis:

$H_0{}_{ABD}:{\gamma }_{ijk}{}^{ABD}\text{'}\text{s}=0$

That is, there is no significant difference in the extent of color change due to the interaction between fabric, exposure type and fabric direction.

Alternative hypothesis:

$H_a{}_{ABD}:\text{At least one of }{\gamma }_{ijk}{}^{ABD}\text{'}\text{s}\ne 0$

That is, there is a significant difference in the extent of color change due to the interaction between fabric, exposure type and fabric direction.

Testing the Hypothesis for the interaction effect ACD:

Null hypothesis:

$H_0{}_{ACD}:{\gamma }_{ijk}{}^{ACD}\text{'}\text{s}=0$

That is, there is no significant difference in the extent of color change due to the interaction between fabric, exposure level and fabric direction.

Alternative hypothesis:

$H_a{}_{ACD}:\text{At least one of }{\gamma }_{ijk}{}^{ACD}\text{'}\text{s}\ne 0$

That is, there is a significant difference in the extent of color change due to the interaction between fabric, exposure level and fabric direction.

Testing the Hypothesis for the interaction effect BCD:

Null hypothesis:

$H_0{}_{BCD}:{\gamma }_{ijk}{}^{BCD}\text{'}\text{s}=0$

That is, there is no significant difference in the extent of color change due to the interaction between exposure type, exposure level and fabric direction.

Alternative hypothesis:

$H_a{}_{BCD}:\text{At least one of }{\gamma }_{ijk}{}^{BCD}\text{'}\text{s}\ne 0$

That is, there is a significant difference in the extent of color change due to the interaction between exposure type, exposure level and fabric direction.

Testing the Hypothesis for the interaction effect ABCD:

Null hypothesis:

$H_0{}_{ABCD}:{\gamma }_{ijkp}{}^{ABCD}\text{'}\text{s}=0$

That is, there is no significant difference in the extent of color change due to the interaction between exposure type, exposure level and fabric direction.

Alternative hypothesis:

$H_{aA}{}_{BCD}:\text{At least one of }{\gamma }_{ijkp}{}^{ABCD}\text{'}\text{s}\ne 0$

That is, there is a significant difference in the extent of color change due to the interaction between fabric, exposure type, exposure level and fabric direction.

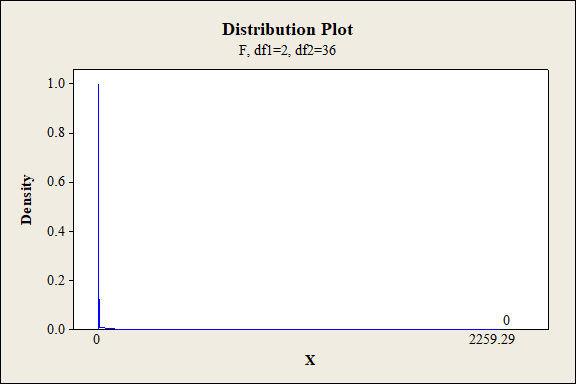
P-value for the main effect of A:

Software procedure:

Step-by-step procedure to find the P-value is given below:

• Click on Graph, select View Probability and click OK.
• Select F, enter 2 in numerator df and 36 in denominator df.
• Under Shaded Area Tab select X value under Define Shaded Area By and select right tails.
• Choose X value as 2,259.29.
• Click OK.

Output obtained from MINITAB is given below:

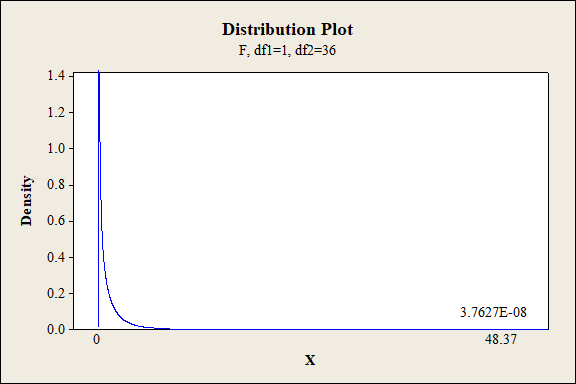
P-value for the main effect of B:

Software procedure:

Step-by-step procedure to find the P-value is given below:

• Click on Graph, select View Probability and click OK.
• Select F, enter 1 in numerator df and 36 in denominator df.
• Under Shaded Area Tab select X value under Define Shaded Area By and select right tails.
• Choose X value as 48.37.
• Click OK.

Output obtained from MINITAB is given below:

P-value for the main effect of C:

Software procedure:

Step-by-step procedure to find the P-value is given below:

• Click on Graph, select View Probability and click OK.
• Select F, enter 2 in numerator df and 36 in denominator df.
• Under Shaded Area Tab select X value under Define Shaded Area By and select right tails.
• Choose X value as 503.36.
• Click OK.

Output obtained from MINITAB is given below:

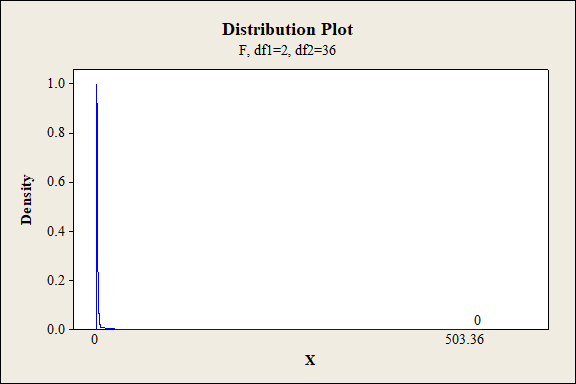
P-value for the main effect of D:

Software procedure:

Step-by-step procedure to find the P-value is given below:

• Click on Graph, select View Probability and click OK.
• Select F, enter 1 in numerator df and 36 in denominator df.
• Under Shaded Area Tab select X value under Define Shaded Area By and select right tails.
• Choose X value as 0.05.
• Click OK.

Output obtained from MINITAB is given below:

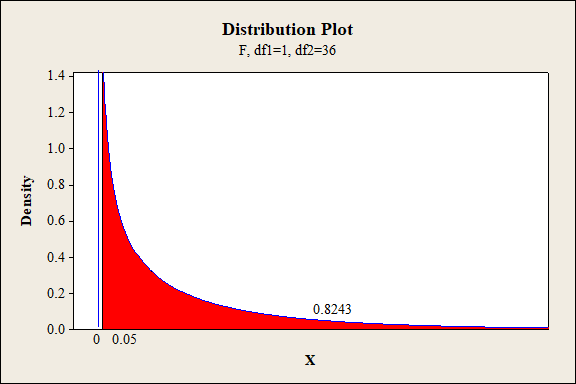
P-value for the interaction effect of A and B:

Software procedure:

Step-by-step procedure to find the P-value is given below:

• Click on Graph, select View Probability and click OK.
• Select F, enter 2 in numerator df and 36 in denominator df.
• Under Shaded Area Tab select X value under Define Shaded Area By and select right tails.
• Choose X value as 15.66.
• Click OK.

Output obtained from MINITAB is given below:

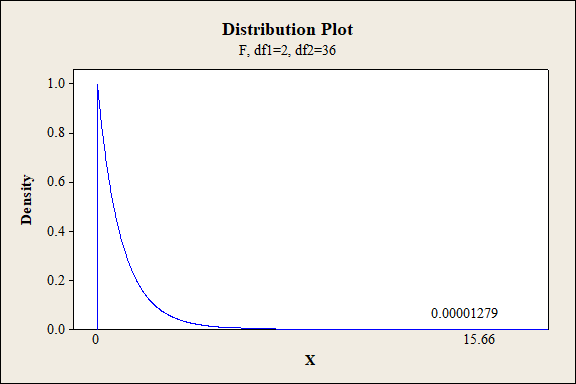
P-value for the interaction effect of A and C:

Software procedure:

Step-by-step procedure to find the P-value is given below:

• Click on Graph, select View Probability and click OK.
• Select F, enter 4 in numerator df and 36 in denominator df.
• Under Shaded Area Tab select X value under Define Shaded Area By and select right tails.
• Choose X value as 281.93.
• Click OK.

Output obtained from MINITAB is given below:

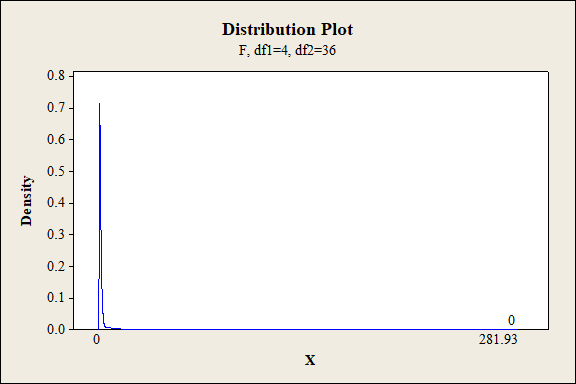
P-value for the interaction effect of A and D:

Software procedure:

Step-by-step procedure to find the P-value is given below:

• Click on Graph, select View Probability and click OK.
• Select F, enter 2 in numerator df and 36 in denominator df.
• Under Shaded Area Tab select X value under Define Shaded Area By and select right tails.
• Choose X value as 0.48.
• Click OK.

Output obtained from MINITAB is given below:

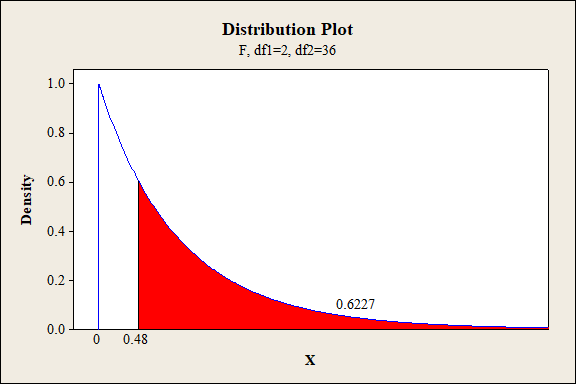
P-value for the interaction effect of B and C:

Software procedure:

Step-by-step procedure to find the P-value is given below:

• Click on Graph, select View Probability and click OK.
• Select F, enter 2 in numerator df and 36 in denominator df.
• Under Shaded Area Tab select X value under Define Shaded Area By and select right tails.
• Choose X value as 2.19.
• Click OK.

Output obtained from MINITAB is given below:

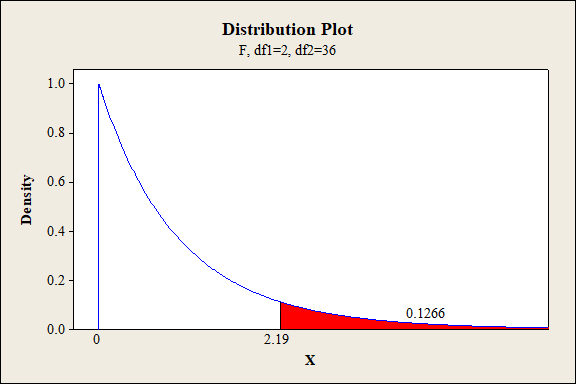
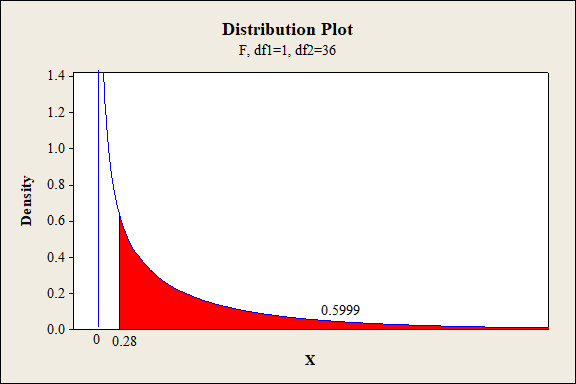
P-value for the interaction effect of B and D:

Software procedure:

Step-by-step procedure to find the P-value is given below:

• Click on Graph, select View Probability and click OK.
• Select F, enter 1 in numerator df and 36 in denominator df.
• Under Shaded Area Tab select X value under Define Shaded Area By and select right tails.
• Choose X value as 0.28.
• Click OK.

Output obtained from MINITAB is given below:

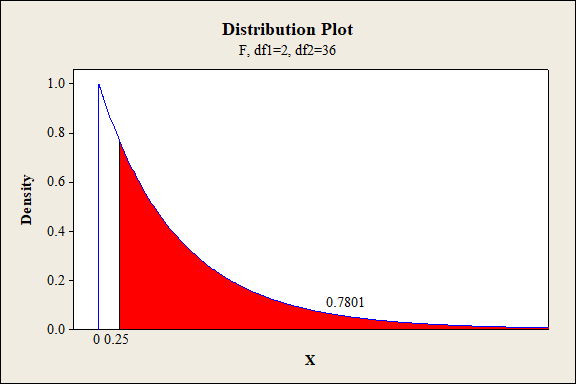
P-value for the interaction effect of C and D:

Software procedure:

Step-by-step procedure to find the P-value is given below:

• Click on Graph, select View Probability and click OK.
• Select F, enter 2 in numerator df and 36 in denominator df.
• Under Shaded Area Tab select X value under Define Shaded Area By and select right tails.
• Choose X value as 0.25.
• Click OK.

Output obtained from MINITAB is given below:

P-value for the interaction effect of A, B and C:

Software procedure:

Step-by-step procedure to find the P-value is given below:

• Click on Graph, select View Probability and click OK.
• Select F, enter 4 in numerator df and 36 in denominator df.
• Under Shaded Area Tab select X value under Define Shaded Area By and select right tails.
• Choose X value as 3.80.
• Click OK.

Output obtained from MINITAB is given below:

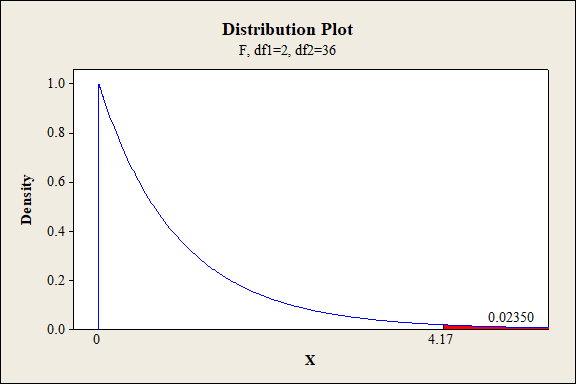
P-value for the interaction effect of A, B and D:

Software procedure:

Step-by-step procedure to find the P-value is given below:

• Click on Graph, select View Probability and click OK.
• Select F, enter 2 in numerator df and 36 in denominator df.
• Under Shaded Area Tab select X value under Define Shaded Area By and select right tails.
• Choose X value as 4.17.
• Click OK.

Output obtained from MINITAB is given below:

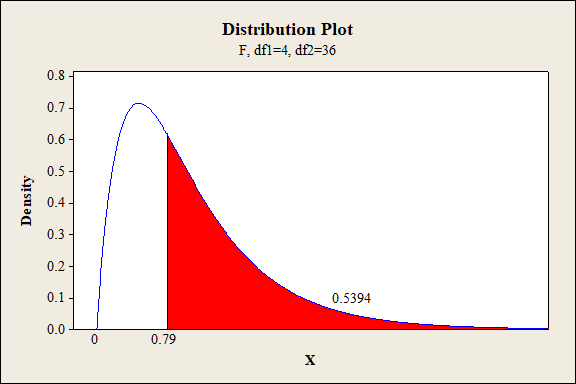
P-value for the interaction effect of A, C and D:

Software procedure:

Step-by-step procedure to find the P-value is given below:

• Click on Graph, select View Probability and click OK.
• Select F, enter 4 in numerator df and 36 in denominator df.
• Under Shaded Area Tab select X value under Define Shaded Area By and select right tails.
• Choose X value as 0.79.
• Click OK.

Output obtained from MINITAB is given below:

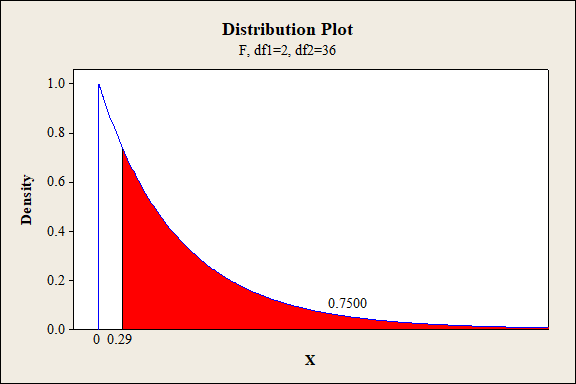
P-value for the interaction effect of B, C and D:

Software procedure:

Step-by-step procedure to find the P-value is given below:

• Click on Graph, select View Probability and click OK.
• Select F, enter 2 in numerator df and 36 in denominator df.
• Under Shaded Area Tab select X value under Define Shaded Area By and select right tails.
• Choose X value as 0.29.
• Click OK.

Output obtained from MINITAB is given below:

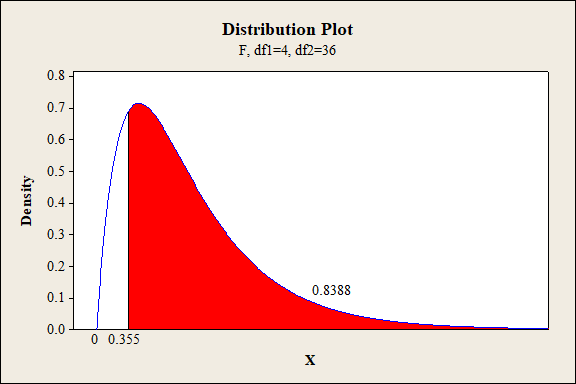
P-value for the interaction effect of A, B, C and D:

Software procedure:

Step-by-step procedure to find the P-value is given below:

• Click on Graph, select View Probability and click OK.
• Select F, enter 4 in numerator df and 36 in denominator df.
• Under Shaded Area Tab select X value under Define Shaded Area By and select right tails.
• Choose X value as 0.355.
• Click OK.

Output obtained from MINITAB is given below:

Conclusion:

For the main effect of A:

The P- value for the factor A (fabric) is 0.000 and the level of significance is 0.01.

Here, the P- value is lesser than the level of significance.

That is, $0.000\left(=P\text{-value}\right)<0.01\left(=\alpha \right)$.

Thus, the null hypothesis is rejected,

Hence, there is sufficient of evidence to conclude that there is an effect of fabric on the extent of color change at 1% level of significance.

For main effect of B:

The P- value for the factor B (exposure level) is 0.000 and the level of significance is 0.01.

Here, the P- value is lesser than the level of significance.

That is, $0.000\left(=P\text{-value}\right)<0.01\left(=\alpha \right)$.

Thus, the null hypothesis is not rejected.

Hence, there is sufficient of evidence to conclude that there is an effect exposure type on the extent of color change at 1% level of significance.

For main effect of C:

The P- value for the factor C (exposure level) is 0.000 and the level of significance is 0.01.

Here, the P- value is lesser than the level of significance.

That is, $0.000\left(=P\text{-value}\right)<0.01\left(=\alpha \right)$.

Thus, the null hypothesis is rejected.

Hence, there is sufficient of evidence to conclude that there is an effect of exposure level on the extent of color change at 1% level of significance.

For main effect of D:

The P- value for the factor D (fabric direction) is 0.8243 and the level of significance is 0.01.

Here, the P- value is greater than the level of significance.

That is, $0.8243\left(=P\text{-value}\right)>0.01\left(=\alpha \right)$.

Thus, the null hypothesis is not rejected.

Hence, there is no sufficient of evidence to conclude that there is an effect of fabric direction on the extent of color change at 1% level of significance.

Interaction effect of factor A and B:

The P- value for the interaction effect AB (fabric and exposure type) is 0.000 and the level of significance is 0.01.

Here, the P- value is lesser than the level of significance.

That is, $0.000\left(=P\text{-value}\right)<0.01\left(=\alpha \right)$.

Thus, the null hypothesis is rejected,

Hence, there is sufficient of evidence to conclude that there is an interaction effect of fabric and exposure type on the extent of color change at 1% level of significance.

Interaction effect of factor A and C:

The P- value for the interaction effect AC (fabric and exposure level) is 0.000 and the level of significance is 0.01.

Here, the P- value is lesser than the level of significance.

That is, $0.000\left(=P\text{-value}\right)<0.01\left(=\alpha \right)$.

Thus, the null hypothesis is rejected.

Hence, there is sufficient of evidence to conclude that there is an interaction effect of fabric and exposure level on the extent of color change at 1% level of significance.

Interaction effect of factor A and D:

The P- value for the interaction effect AD (fabric and fabric direction) is 0.6227 and the level of significance is 0.01.

Here, the P- value is greater than the level of significance.

That is, $0.6227\left(=P\text{-value}\right)>0.01\left(=\alpha \right)$.

Thus, the null hypothesis is not rejected.

Hence, there is no sufficient of evidence to conclude that there is an interaction effect of fabric and fabric direction on the extent of color change at 1% level of significance.

Interaction effect of factor B and C:

The P- value for the interaction effect BC (exposure type and exposure level) is 0.1266 and the level of significance is 0.01.

Here, the P- value is greater than the level of significance.

That is, $0.1266\left(=P\text{-value}\right)>0.01\left(=\alpha \right)$.

Thus, the null hypothesis is not rejected,

Hence, there is no sufficient of evidence to conclude that there is an interaction effect of exposure type and exposure level on the extent of color change at 1% level of significance.

Interaction effect of factor B and D:

The P- value for the interaction effect BD (exposure type and fabric direction) is 0.5999 and the level of significance is 0.01.

Here, the P- value is greater than the level of significance.

That is, $0.5999\left(=P\text{-value}\right)>0.01\left(=\alpha \right)$.

Thus, the null hypothesis is not rejected,

Hence, there is no sufficient of evidence to conclude that there is an interaction effect of exposure type and fabric direction on the extent of color change at 1% level of significance.

Interaction effect of factor C and D:

The P- value for the interaction effect CD (exposure level and fabric direction) is 0.7801 and the level of significance is 0.01.

Here, the P- value is greater than the level of significance.

That is, $0.7801\left(=P\text{-value}\right)>0.01\left(=\alpha \right)$.

Thus, the null hypothesis is not rejected,

Hence, there is no sufficient of evidence to conclude that there is an interaction effect of exposure level and fabric direction on the extent of color change at 1% level of significance.

Interaction effect of factor A,B and C:

The P- value for the interaction effect ABC (fabric, exposure type and exposure level) is 0.01119 and the level of significance is 0.01.

Here, the P- value is greater than the level of significance.

That is, $0.1119\left(=P\text{-value}\right)>0.01\left(=\alpha \right)$.

Thus, the null hypothesis is not rejected.

Hence, there is no sufficient of evidence to conclude that there is an interaction effect of fabric, exposure type and exposure level on the extent of color change at 1% level of significance.

Interaction effect of factor A,B and D:

The P- value for the interaction effect ABD (fabric, exposure type and fabric direction) is 0.0235 and the level of significance is 0.01.

Here, the P- value is greater than the level of significance.

That is, $0.0235\left(=P\text{-value}\right)>0.01\left(=\alpha \right)$.

Thus, the null hypothesis is not rejected.

Hence, there is no sufficient of evidence to conclude that there is an interaction effect of fabric, exposure type and fabric direction on the extent of color change at 1% level of significance.

Interaction effect of factor A,C and D:

The P- value for the interaction effect ACD (fabric, exposure level and fabric direction) is 0.5394 and the level of significance is 0.01.

Here, the P- value is greater than the level of significance.

That is, $0.5394\left(=P\text{-value}\right)>0.01\left(=\alpha \right)$.

Thus, the null hypothesis is not rejected.

Hence, there is no sufficient of evidence to conclude that there is an interaction effect of fabric, exposure level and fabric direction on the extent of color change at 1% level of significance.

Interaction effect of factor B, C and D:

The P- value for the interaction effect BCD (exposure type, exposure level and fabric direction) is 0.7500 and the level of significance is 0.01.

Here, the P- value is greater than the level of significance.

That is, $0.7500\left(=P\text{-value}\right)>0.01\left(=\alpha \right)$.

Thus, the null hypothesis is not rejected.

Hence, there is no sufficient of evidence to conclude that there is an interaction effect of exposure type, exposure level and fabric direction on the extent of color change at 1% level of significance.

Interaction effect of factor A, B, C and D:

The P- value for the interaction effect ABCD (fabric, exposure type, exposure level and fabric direction) is 0.8388 and the level of significance is 0.01.

Here, the P- value is greater than the level of significance.

That is, $0.8388\left(=P\text{-value}\right)>0.01\left(=\alpha \right)$.

Thus, the null hypothesis is not rejected.

Hence, there is no sufficient of evidence to conclude that there is an interaction effect of fabric, exposure type, exposure level and fabric direction on the extent of color change at 1% level of significance.

Therefore, there is significant difference in the extent of color change with respect to the main effect A, B, D and interaction effects AB, AC are significant at 1% level of significance. The remaining second order interactions and third order interaction are not significant at 1% level of significance.