Chapter 11.3, Problem 13AYU

NW Ramp Metering Ramp metering is a traffic engineering idea that requires cars entering a freeway to stop for a certain period of time before joining the traffic flow. The theory is that ramp metering controls the number of cars on the freeway and the number of cars accessing the freeway, resulting in a freer flow of cars, which ultimately results in faster travel times. To test whether ramp metering is effective in reducing travel times, engineers in Minneapolis, Minnesota, conducted an experiment in which a section of freeway had ramp meters installed on the on-ramps. The response variable for the study was speed of the vehicles. A random sample of 15 cars on the highway for a Monday at 6 P.M. with the ramp meters on and a second random sample of 15 cars on a different Monday at 6 P.M. with the meters off resulted in the following speeds (in miles per hour).

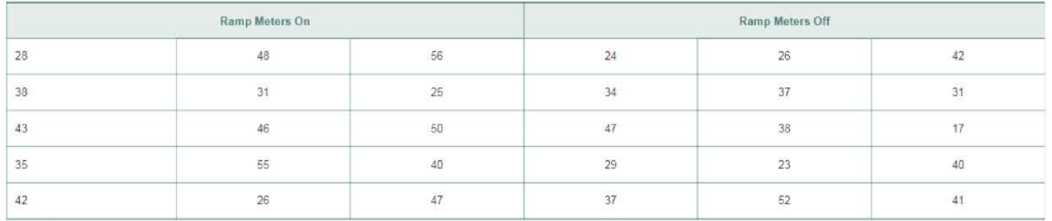
1. a. Draw side-by-side boxplots of each data set. Does there appear to be a difference in the speeds? Are there any outliers?
2. b. Are the ramp meters effective in maintaining a higher speed on the freeway? Use the α = 0.10 level of significance.