
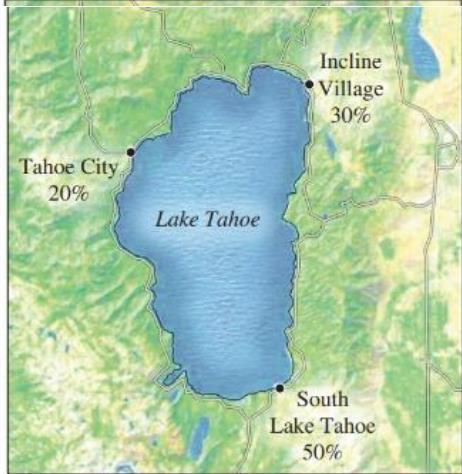
Store location two competitive pet shops want to open stores at Lake Tahoe, where there are currently no pet shops. The following figure shows the percentages of the total Tahoe population serviced by each of the three main business centers. If both shops open in the same business center, then they split all the business equally; if they open in two different centers, then they each get all the business in the center in which they open plus half the business in the third center. Where should the two pet shops open? Set up a game matrix and solve.
Want to see the full answer?
Check out a sample textbook solution
Chapter 11 Solutions
EP FINITE MATH.F/BUS,ECON,LIFE..-ACCESS
Additional Math Textbook Solutions
Elementary Statistics (13th Edition)
Algebra and Trigonometry (6th Edition)
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Calculus: Early Transcendentals (2nd Edition)
College Algebra (7th Edition)
Basic Business Statistics, Student Value Edition
- 3. Differentiate the following functions. Show your work where applicable. a) y = e³x b) f(x)=2 cos(5x) c) y = 1 - 2 d) y = In|secx| e) f(t) = t² e√t f) f(x) = 1+x x sin x 3arrow_forwardBit in a bind with the matharrow_forwardQuadrilateral BCDE is similar to quadrilateral FGHI. Find the measure of side FG. Round your answer to the nearest tenth if necessary. BCDEFGHI2737.55arrow_forward
- Please help on both Part b) and c) below Thanksarrow_forwardfind the zeros of the function algebraically: f(x) = 9x2 - 3x - 2arrow_forwarda small pond contains eight catfish and six bluegill. If seven fish are caught at random, what is the probability that exactly five catfish have been caught?arrow_forward
- Listen A falling object travels a distance given by the formula d = 6t + 9t2 where d is in feet and t is the time in seconds. How many seconds will it take for the object to travel 112 feet? Round answer to 2 decimal places. (Write the number, not the units). Your Answer:arrow_forwardSolve by the quadratic formula or completing the square to obtain exact solutions. 2 e 104 OA) -16±3√6 B) 8±√10 O c) -8±√10 OD) 8±3√√6 Uarrow_forwardQuestion 14 (1 point) Listen The frame on a picture is 18 in by 22 in outside and is of uniform width. Using algebraic methods, what is the width of the frame if the inner area of the picture shown is 250 in²2? Write answer to 2 decimal places. (Write the number with no units). 18 in Your Answer: 22 inarrow_forward
- ◄ Listen A vacant lot is being converted into a community garden. The garden and a walkway around its perimeter have an area of 560 square feet. Find the width of the walkway (x) if the garden measures 15 feet wide by 19 feet long. Write answer to 2 decimal places. (Write the number without units). X 15 feet Your Answer: 19 feet Xarrow_forwardListen A stuntman jumps from a roof 440 feet from the ground. How long will it take him to reach the ground? Use the formula, distance, d = 16t2, (where t is in seconds). Write answer to 1 decimal place. (Write the number, not the units). Your Answer:arrow_forwardSolve x² - 10x + 24 = 0 ○ A) 4,6 B) -12, -2 C) 12,2 D) -4, -6arrow_forward
 Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt





