
The spreadsheet summarizes the results for one student on a 15-question math test with partial credit awarded.
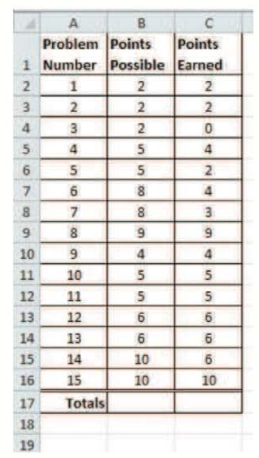
Complete the totals at the bottom of each column using addition.
To calculate: The total of possible points and points earned in the following table:
| Problem number | Points possible | Points earned |
| 1 | 2 | 2 |
| 2 | 2 | 2 |
| 3 | 2 | 0 |
| 4 | 5 | 4 |
| 5 | 5 | 2 |
| 6 | 8 | 4 |
| 7 | 8 | 3 |
| 8 | 9 | 9 |
| 9 | 4 | 4 |
| 10 | 5 | 5 |
| 11 | 5 | 5 |
| 12 | 6 | 6 |
| 13 | 6 | 6 |
| 14 | 10 | 6 |
| 15 | 10 | 10 |
| Totals |
Answer to Problem 1G
Solution:
The total of possible points is
Explanation of Solution
Given Information:
The provided table shows points earned by a student in
| Problem number | Points possible | Points earned |
| 1 | 2 | 2 |
| 2 | 2 | 2 |
| 3 | 2 | 0 |
| 4 | 5 | 4 |
| 5 | 5 | 2 |
| 6 | 8 | 4 |
| 7 | 8 | 3 |
| 8 | 9 | 9 |
| 9 | 4 | 4 |
| 10 | 5 | 5 |
| 11 | 5 | 5 |
| 12 | 6 | 6 |
| 13 | 6 | 6 |
| 14 | 10 | 6 |
| 15 | 10 | 10 |
| Totals |
Calculation:
The total of possible points is sum of all the numbers in the column of possible points.
That is,
Now, the total earned points is sum of all the numbers in the column of earned points.
That is,
Therefore, total possible is points is
Want to see more full solutions like this?
Chapter 1 Solutions
Pathways to Math Literacy (Loose Leaf)
- Q1: A: Let M and N be two subspace of finite dimension linear space X, show that if M = N then dim M = dim N but the converse need not to be true. B: Let A and B two balanced subsets of a linear space X, show that whether An B and AUB are balanced sets or nor. Q2: Answer only two A:Let M be a subset of a linear space X, show that M is a hyperplane of X iff there exists ƒ€ X'/{0} and a € F such that M = (x = x/f&x) = x}. fe B:Show that every two norms on finite dimension linear space are equivalent C: Let f be a linear function from a normed space X in to a normed space Y, show that continuous at x, E X iff for any sequence (x) in X converge to Xo then the sequence (f(x)) converge to (f(x)) in Y. Q3: A:Let M be a closed subspace of a normed space X, constract a linear space X/M as normed space B: Let A be a finite dimension subspace of a Banach space X, show that A is closed. C: Show that every finite dimension normed space is Banach space.arrow_forwardpls helparrow_forwardpls helparrow_forward
 Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt Elementary AlgebraAlgebraISBN:9780998625713Author:Lynn Marecek, MaryAnne Anthony-SmithPublisher:OpenStax - Rice University
Elementary AlgebraAlgebraISBN:9780998625713Author:Lynn Marecek, MaryAnne Anthony-SmithPublisher:OpenStax - Rice University


