MATHEMATICS FOR THE TRADES MYMATHLAB AC
MATHEMATICS FOR THE TRADES MYMATHLAB AC
11th Edition
ISBN: 9780135902028
Author: SAUNDERS
Publisher: PEARSON
bartleby

Concept explainers

Statements and Logic
Logic is the analysis of general patterns of thoughts without regard to any specific sense of context.
bartleby

Videos

Textbook Question
Book Icon
Chapter 1.1, Problem 5EE

E. Calculator Problems

You probably own a calculator and, of course, you are eager to put it to work doing practical math calculations. In this text we include problem sets for calculator users. These problems are taken from real-life situations and, unlike most textbook problems, involve big numbers and lots of calculations. If you think that having an electronic brain-in-a-box means that you do not need to know basic arithmetic, you will be disappointed. The calculator helps you to work faster, but it will not tell you what to do or how to do it.

Detailed instructions on using a calculator with whole numbers appears on page 68.

Here are a few helpful hints for calculator users:

  1. 1. Always estimate your answer before doing a calculation.
  2. 2. Check your answer by comparing it with the estimate or by the other methods shown in this text. Be certain that your answer makes sense.
  3. 3. If you doubt the calculator (they do break down, you know), put a problem in it whose answer you know, preferably a problem like the one you are solving.

Electrical Trades A mapper is a person employed by an electrical utility company who has the job of reading diagrams of utility installations and listing the materials to be installed or removed by engineers. Part of a typical job list might look like this:

INSTALLATION (in feet of conductor)

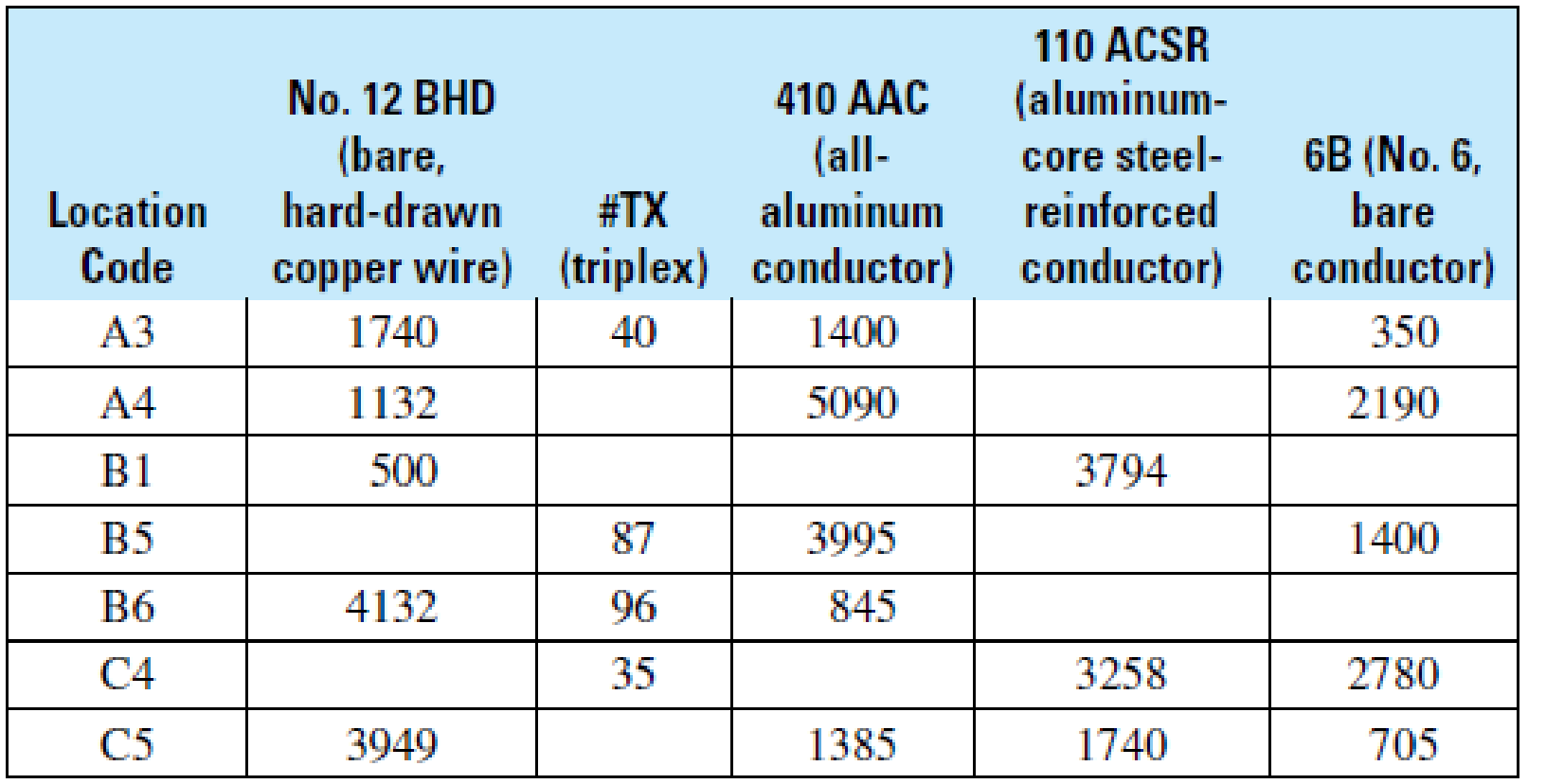
Chapter 1.1, Problem 5EE, E. Calculator Problems You probably own a calculator and, of course, you are eager to put it to work

  1. (a) How many total feet of each kind of conductor must the installer have to complete the job?
  2. (b) How many feet of conductor are to be installed at each of the seven locations?
Expert Solution & Answer
Check Mark

Want to see the full answer?

Check out a sample textbook solution
Blurred answer
Previous
Chapter 1.1, Problem 4EE
Next
Chapter 1.2, Problem 1LC
Students have asked these similar questions
(b) State Fubini's Theorem without proof. Theorem to demonstrate that
(b) Define a simple random variable. Provide an example.
19. Let X be a non-negative random variable. Show that lim nE (IX >n)) = 0. E lim (x)-0. = >

Chapter 1 Solutions

MATHEMATICS FOR THE TRADES MYMATHLAB AC

Ch. 1.1 - Write in numerical form: two hundred six thousand,...Ch. 1.1 - Round the number in problem 1 to the nearest...Ch. 1.1 - Reading, Writing, and Rounding Whole Numbers Write...Ch. 1.1 - Reading, Writing, and Rounding Whole Numbers Write...Ch. 1.1 - Reading, Writing, and Rounding Whole Numbers Write...Ch. 1.1 - Reading, Writing, and Rounding Whole Numbers Write...Ch. 1.1 - Reading, Writing, and Rounding Whole Numbers Write...Ch. 1.1 - Reading, Writing, and Rounding Whole Numbers Write...Ch. 1.1 - Reading, Writing, and Rounding Whole Numbers Write...Ch. 1.1 - Reading, Writing, and Rounding Whole Numbers Write...
Ch. 1.1 - Reading, Writing, and Rounding Whole Numbers Write...Ch. 1.1 - Reading, Writing, and Rounding Whole Numbers Write...Ch. 1.1 - Write as numbers. Three thousand, sixCh. 1.1 - Write as numbers. Seventeen thousand, twenty-fourCh. 1.1 - Write as numbers. Eleven thousand, one hundredCh. 1.1 - Write as numbers. Three million, two thousand,...Ch. 1.1 - Write as numbers. Four million, forty thousand,...Ch. 1.1 - Prob. 16AECh. 1.1 - Round as indicated. 357 to the nearest tenCh. 1.1 - Round as indicated. 4386 to the nearest hundredCh. 1.1 - Round as indicated. 4386 to the nearest thousandCh. 1.1 - Round as indicated. 15,472 to the nearest thousandCh. 1.1 - Round as indicated. 225,799 to the nearest ten...Ch. 1.1 - Round as indicated. 32,408,792 to the nearest...Ch. 1.1 - Add. 4722_Ch. 1.1 - Add. 2731_Ch. 1.1 - Add. 4535_Ch. 1.1 - Add. 3855_Ch. 1.1 - Add. 7548_Ch. 1.1 - Add. 2698_Ch. 1.1 - Add. 4884_Ch. 1.1 - Add. 6769_Ch. 1.1 - Add. 74759_Ch. 1.1 - Add. 50895_Ch. 1.1 - Prob. 11BECh. 1.1 - Add. 432399_Ch. 1.1 - Add. 621388_Ch. 1.1 - Add. 189204_Ch. 1.1 - Add. 375486_Ch. 1.1 - Add. 4237288_Ch. 1.1 - Prob. 17BECh. 1.1 - Prob. 18BECh. 1.1 - Add. 37857643_Ch. 1.1 - Prob. 20BECh. 1.1 - Add. 10674397_Ch. 1.1 - Add. 400267085_Ch. 1.1 - Prob. 23BECh. 1.1 - Add. 198764835_Ch. 1.1 - Add. 7804497684_Ch. 1.1 - Prob. 26BECh. 1.1 - Add. 581824433_Ch. 1.1 - Prob. 28BECh. 1.1 - Prob. 29BECh. 1.1 - B. Add.Ch. 1.1 - C. Arrange vertically and find the sum. 487 + 29 +...Ch. 1.1 - Prob. 2CECh. 1.1 - C. Arrange vertically and find the sum. 322 + 46 +...Ch. 1.1 - C. Arrange vertically and find the sum. 7268 + 209...Ch. 1.1 - Prob. 5CECh. 1.1 - C. Arrange vertically and find the sum. 715 + 4293...Ch. 1.1 - C. Arrange vertically and find the sum....Ch. 1.1 - C. Arrange vertically and find the sum....Ch. 1.1 - C. Arrange vertically and find the sum....Ch. 1.1 - C. Arrange vertically and find the sum....Ch. 1.1 - Prob. 11CECh. 1.1 - C. Arrange vertically and find the sum....Ch. 1.1 - Prob. 13CECh. 1.1 - C. Arrange vertically and find the sum....Ch. 1.1 - Prob. 15CECh. 1.1 - C. Arrange vertically and find the sum....Ch. 1.1 - C. Arrange vertically and find the sum....Ch. 1.1 - C. Arrange vertically and find the sum....Ch. 1.1 - Prob. 19CECh. 1.1 - C. Arrange vertically and find the sum....Ch. 1.1 - D. Practical Applications. Electrical Trades In...Ch. 1.1 - D. Practical Applications. Flooring and Carpeting...Ch. 1.1 - D. Practical Applications. Machine Trades The...Ch. 1.1 - D. Practical Applications. Trades Management In...Ch. 1.1 - D. Practical Applications. Trades Management The...Ch. 1.1 - D. Practical Applications. Roofing On a home...Ch. 1.1 - Prob. 7DECh. 1.1 - D. Practical Applications. Automotive Trades A...Ch. 1.1 - D. Practical Applications. Construction The Happy...Ch. 1.1 - D. Practical Applications. Machine Trades A...Ch. 1.1 - D. Practical Applications. Landscaping A new...Ch. 1.1 - Prob. 12DECh. 1.1 - D. Practical Applications. Electronics When...Ch. 1.1 - Prob. 14DECh. 1.1 - Prob. 15DECh. 1.1 - D. Practical Applications. Allied Health The...Ch. 1.1 - D. Practical Applications. Construction For...Ch. 1.1 - D. Practical Applications. Automotive Trades The...Ch. 1.1 - D. Practical Applications. Sports and Leisure In...Ch. 1.1 - Prob. 1EECh. 1.1 - E. Calculator Problems You probably own a...Ch. 1.1 - E. Calculator Problems You probably own a...Ch. 1.1 - E. Calculator Problems You probably own a...Ch. 1.1 - E. Calculator Problems You probably own a...Ch. 1.2 - Do the following without using a calculator: Add:...Ch. 1.2 - Do the following without using a calculator:...Ch. 1.2 - Subtract. 427_Ch. 1.2 - Prob. 2AECh. 1.2 - Subtract. 349_Ch. 1.2 - Prob. 4AECh. 1.2 - Prob. 5AECh. 1.2 - Prob. 6AECh. 1.2 - Prob. 7AECh. 1.2 - Subtract. 9622_Ch. 1.2 - Prob. 9AECh. 1.2 - Prob. 10AECh. 1.2 - Prob. 11AECh. 1.2 - Subtract. 3617_Ch. 1.2 - Prob. 13AECh. 1.2 - Subtract. 5216_Ch. 1.2 - Subtract. 6527_Ch. 1.2 - Prob. 16AECh. 1.2 - Prob. 17AECh. 1.2 - Subtract. 7048_Ch. 1.2 - Subtract. 349_Ch. 1.2 - Prob. 20AECh. 1.2 - Subtract. 546357_Ch. 1.2 - Prob. 22AECh. 1.2 - Prob. 23AECh. 1.2 - Prob. 24AECh. 1.2 - Prob. 25AECh. 1.2 - Prob. 26AECh. 1.2 - Prob. 27AECh. 1.2 - Prob. 28AECh. 1.2 - Prob. 29AECh. 1.2 - Prob. 30AECh. 1.2 - Prob. 31AECh. 1.2 - Prob. 32AECh. 1.2 - Prob. 33AECh. 1.2 - Prob. 34AECh. 1.2 - Subtract. 5007266_Ch. 1.2 - Prob. 36AECh. 1.2 - Prob. 37AECh. 1.2 - Prob. 38AECh. 1.2 - Prob. 1BECh. 1.2 - Prob. 2BECh. 1.2 - Prob. 3BECh. 1.2 - Prob. 4BECh. 1.2 - Prob. 5BECh. 1.2 - Prob. 6BECh. 1.2 - Prob. 7BECh. 1.2 - Prob. 8BECh. 1.2 - B. Practical Applications Automotive Trades A...Ch. 1.2 - B. Practical Applications Construction A truck...Ch. 1.2 - Prob. 11BECh. 1.2 - Prob. 12BECh. 1.2 - Prob. 13BECh. 1.2 - Prob. 14BECh. 1.2 - B Practical Applications Electronics An electronic...Ch. 1.2 - B Practical Applications Automotive Trades A set...Ch. 1.2 - Prob. 17BECh. 1.2 - B Practical Applications General Interest The...Ch. 1.2 - B Practical Applications Life Skills A potential...Ch. 1.2 - C. Calculator Problems Plumbing The Karroll...Ch. 1.2 - C. Calculator Problems Which sum is greater?Ch. 1.2 - C. Calculator Problems Trades Management If an...Ch. 1.2 - C. Calculator Problems Trades Management The...Ch. 1.2 - C. Calculator Problems Life Skills Balance the...Ch. 1.2 - C. Calculator Problems Construction A water meter...Ch. 1.3 - Subtract: 572286Ch. 1.3 - Multiply: 69Ch. 1.3 - Prob. 1AECh. 1.3 - Multiply. 78_Ch. 1.3 - Prob. 3AECh. 1.3 - Prob. 4AECh. 1.3 - Prob. 5AECh. 1.3 - Prob. 6AECh. 1.3 - Prob. 7AECh. 1.3 - Prob. 8AECh. 1.3 - Prob. 9AECh. 1.3 - Prob. 10AECh. 1.3 - Prob. 11AECh. 1.3 - Prob. 12AECh. 1.3 - Prob. 13AECh. 1.3 - Prob. 14AECh. 1.3 - Prob. 15AECh. 1.3 - Prob. 16AECh. 1.3 - Prob. 17AECh. 1.3 - Prob. 18AECh. 1.3 - Prob. 19AECh. 1.3 - Prob. 20AECh. 1.3 - Prob. 21AECh. 1.3 - Prob. 22AECh. 1.3 - Multiply. 7211_Ch. 1.3 - Prob. 24AECh. 1.3 - Prob. 25AECh. 1.3 - Prob. 26AECh. 1.3 - Prob. 27AECh. 1.3 - Prob. 28AECh. 1.3 - Prob. 29AECh. 1.3 - Prob. 30AECh. 1.3 - Prob. 31AECh. 1.3 - Multiply. 6625_Ch. 1.3 - Prob. 33AECh. 1.3 - Prob. 34AECh. 1.3 - Prob. 35AECh. 1.3 - Prob. 36AECh. 1.3 - Prob. 1BECh. 1.3 - Multiply. 6097_Ch. 1.3 - Prob. 3BECh. 1.3 - Prob. 4BECh. 1.3 - Prob. 5BECh. 1.3 - Prob. 6BECh. 1.3 - Prob. 7BECh. 1.3 - Prob. 8BECh. 1.3 - Prob. 9BECh. 1.3 - Prob. 10BECh. 1.3 - Prob. 11BECh. 1.3 - Prob. 12BECh. 1.3 - Prob. 13BECh. 1.3 - Multiply. 542600_Ch. 1.3 - Multiply. 7009504_Ch. 1.3 - Prob. 16BECh. 1.3 - Prob. 17BECh. 1.3 - Prob. 18BECh. 1.3 - Prob. 19BECh. 1.3 - Prob. 20BECh. 1.3 - Prob. 1CECh. 1.3 - Prob. 2CECh. 1.3 - Prob. 3CECh. 1.3 - Prob. 4CECh. 1.3 - Prob. 5CECh. 1.3 - Prob. 6CECh. 1.3 - Prob. 7CECh. 1.3 - Practical Applications Construction What is the...Ch. 1.3 - Prob. 9CECh. 1.3 - Prob. 10CECh. 1.3 - Prob. 11CECh. 1.3 - Prob. 12CECh. 1.3 - Practical Applications Machine Trades If a machine...Ch. 1.3 - C. Practical Applications Electronics For a...Ch. 1.3 - C. Practical Applications Roofing In the Happy...Ch. 1.3 - C. Practical Applications Electronics A 78-ohm...Ch. 1.3 - Prob. 17CECh. 1.3 - Prob. 18CECh. 1.3 - Prob. 19CECh. 1.3 - Prob. 20CECh. 1.3 - Prob. 21CECh. 1.3 - Prob. 22CECh. 1.3 - Prob. 23CECh. 1.3 - Prob. 24CECh. 1.3 - Prob. 25CECh. 1.3 - Prob. 26CECh. 1.3 - Water/Wastewater Treatment A rural water district...Ch. 1.3 - Prob. 28CECh. 1.3 - Prob. 29CECh. 1.3 - Calculator Problems Business and Finance If an...Ch. 1.3 - Prob. 2DECh. 1.3 - Prob. 3DECh. 1.3 - Prob. 4DECh. 1.3 - Prob. 5DECh. 1.3 - Prob. 6DECh. 1.4 - Multiply: 3845Ch. 1.4 - Prob. 2LCCh. 1.4 - A. Divide. 63 7Ch. 1.4 - Prob. 2AECh. 1.4 - Prob. 3AECh. 1.4 - Prob. 4AECh. 1.4 - A. Divide. 54 9Ch. 1.4 - Prob. 6AECh. 1.4 - A. Divide. 725Ch. 1.4 - Prob. 8AECh. 1.4 - Prob. 9AECh. 1.4 - Prob. 10AECh. 1.4 - Prob. 11AECh. 1.4 - Prob. 12AECh. 1.4 - Prob. 13AECh. 1.4 - Prob. 14AECh. 1.4 - A. Divide. 14767Ch. 1.4 - A. Divide. 7364Ch. 1.4 - Prob. 17AECh. 1.4 - A. Divide. 42018Ch. 1.4 - A. Divide. 92000Ch. 1.4 - A. Divide. 71000Ch. 1.4 - A. Divide. 73507Ch. 1.4 - Prob. 22AECh. 1.4 - Prob. 23AECh. 1.4 - Prob. 24AECh. 1.4 - Divide. 322 14Ch. 1.4 - Prob. 2BECh. 1.4 - Prob. 3BECh. 1.4 - Prob. 4BECh. 1.4 - Prob. 5BECh. 1.4 - Prob. 6BECh. 1.4 - Prob. 7BECh. 1.4 - Prob. 8BECh. 1.4 - B. Divide. 42371Ch. 1.4 - Prob. 10BECh. 1.4 - Prob. 11BECh. 1.4 - Prob. 12BECh. 1.4 - Prob. 13BECh. 1.4 - B. Divide. 2400 75Ch. 1.4 - Prob. 15BECh. 1.4 - Prob. 16BECh. 1.4 - Prob. 17BECh. 1.4 - Prob. 18BECh. 1.4 - Prob. 19BECh. 1.4 - B. Divide. 4794425Ch. 1.4 - Prob. 21BECh. 1.4 - B. Divide. 23114091Ch. 1.4 - Prob. 23BECh. 1.4 - Prob. 24BECh. 1.4 - Prob. 25BECh. 1.4 - Prob. 26BECh. 1.4 - Prob. 27BECh. 1.4 - Prob. 28BECh. 1.4 - Prob. 29BECh. 1.4 - C. For each of the following whole numbers, (a)...Ch. 1.4 - Prob. 2CECh. 1.4 - Prob. 3CECh. 1.4 - Prob. 4CECh. 1.4 - Prob. 5CECh. 1.4 - C. For each of the following whole numbers, (a)...Ch. 1.4 - D. Applied Problems Machine Trades A machinist has...Ch. 1.4 - Prob. 2DECh. 1.4 - Prob. 3DECh. 1.4 - Prob. 4DECh. 1.4 - Prob. 5DECh. 1.4 - Prob. 6DECh. 1.4 - Prob. 7DECh. 1.4 - Prob. 8DECh. 1.4 - Prob. 9DECh. 1.4 - D. Applied Problems Transportation A delivery...Ch. 1.4 - D. Applied Problems Automotive Trades A mechanic...Ch. 1.4 - D. Applied Problems Metalworking One cubic foot of...Ch. 1.4 - D. Applied Problems Printing A printer needs...Ch. 1.4 - D. Applied Problems Water/Wastewater Treatment A...Ch. 1.4 - D. Applied Problems HVAC A geothermal heat pump...Ch. 1.4 - Prob. 16DECh. 1.4 - D. Applied Problems HVAC A family wants to replace...Ch. 1.4 - D. Applied Problems Agriculture Barley weighs 48...Ch. 1.4 - D. Applied Problems Water/Wastewater Treatment A...Ch. 1.4 - D. Applied Problems Electrical Trades A...Ch. 1.4 - D. Applied Problems Carpentry Each 8-foot length...Ch. 1.4 - D. Applied Problems Automotive Trades The...Ch. 1.4 - E. Calculator Problems Calculate the following....Ch. 1.4 - Prob. 2EECh. 1.4 - Prob. 3EECh. 1.4 - Prob. 4EECh. 1.4 - Prob. 5EECh. 1.4 - E. Calculator Problems Painting Following are four...Ch. 1.4 - Prob. 7EECh. 1.5 - Divide 24768Ch. 1.5 - Calculate: 8 4 2Ch. 1.5 - Perform all operations in the correct order. 2 + 8...Ch. 1.5 - Prob. 2AECh. 1.5 - Perform all operations in the correct order. 40 ...Ch. 1.5 - Perform all operations in the correct order. 16 +...Ch. 1.5 - Prob. 5AECh. 1.5 - Prob. 6AECh. 1.5 - Prob. 7AECh. 1.5 - Perform all operations in the correct order. 64 ...Ch. 1.5 - Prob. 9AECh. 1.5 - Prob. 10AECh. 1.5 - Prob. 11AECh. 1.5 - Prob. 12AECh. 1.5 - Prob. 13AECh. 1.5 - Prob. 14AECh. 1.5 - Prob. 15AECh. 1.5 - Prob. 16AECh. 1.5 - Prob. 17AECh. 1.5 - Prob. 18AECh. 1.5 - Prob. 19AECh. 1.5 - Prob. 20AECh. 1.5 - Prob. 21AECh. 1.5 - Perform all operations in the correct order. 54 ...Ch. 1.5 - Perform all operations in the correct order. (4 3...Ch. 1.5 - Prob. 24AECh. 1.5 - Prob. 25AECh. 1.5 - Prob. 26AECh. 1.5 - Prob. 27AECh. 1.5 - Prob. 28AECh. 1.5 - Perform all operations in the correct order. 12 7...Ch. 1.5 - Prob. 30AECh. 1.5 - Prob. 31AECh. 1.5 - Prob. 32AECh. 1.5 - Prob. 33AECh. 1.5 - Prob. 34AECh. 1.5 - Prob. 35AECh. 1.5 - Prob. 36AECh. 1.5 - Prob. 37AECh. 1.5 - Prob. 38AECh. 1.5 - Prob. 39AECh. 1.5 - Prob. 40AECh. 1.5 - Painting A painter ordered 3 gallons of acrylic...Ch. 1.5 - Landscaping On a certain landscaping job, Steve...Ch. 1.5 - Prob. 3BECh. 1.5 - Prob. 4BECh. 1.5 - Prob. 5BECh. 1.5 - Prob. 6BECh. 1.5 - Prob. 7BECh. 1.5 - Prob. 8BECh. 1.5 - Prob. 9BECh. 1.5 - Prob. 10BECh. 1.5 - Prob. 11BECh. 1.5 - C. Calculator Problems 462 + 83 95Ch. 1.5 - Prob. 2CECh. 1.5 - Prob. 3CECh. 1.5 - Prob. 4CECh. 1.5 - Prob. 5CECh. 1.5 - Prob. 6CECh. 1.5 - Prob. 7CECh. 1.5 - Prob. 8CECh. 1.5 - Prob. 9CECh. 1.5 - Prob. 10CECh. 1.5 - C. Calculator Problems 864 16 27Ch. 1.5 - Prob. 12CECh. 1.5 - Prob. 13CECh. 1.5 - Prob. 14CECh. 1.5 - Prob. 15CECh. 1.5 - Prob. 16CECh. 1 - (a) Write whole numbers in words. (b) Write, in...Ch. 1 - Round whole numbers. Round 214,659 (a) to the...Ch. 1 - Add whole numbers. (a) 67 + 58 (b) 7009 + 1598Ch. 1 - Prob. 4PCh. 1 - Prob. 5PCh. 1 - Prob. 6PCh. 1 - Prob. 7PCh. 1 - Use the correct order of operations with addition,...Ch. 1 - Prob. 9PCh. 1 - A. Reading, Writing, and Rounding Whole Numbers...Ch. 1 - A. Reading, Writing, and Rounding Whole Numbers...Ch. 1 - Prob. 3APSCh. 1 - Prob. 4APSCh. 1 - Prob. 5APSCh. 1 - A. Reading, Writing, and Rounding Whole Numbers...Ch. 1 - Prob. 7APSCh. 1 - Prob. 8APSCh. 1 - Prob. 9APSCh. 1 - Prob. 10APSCh. 1 - Prob. 11APSCh. 1 - Prob. 12APSCh. 1 - Prob. 13APSCh. 1 - Prob. 14APSCh. 1 - Prob. 15APSCh. 1 - A. Reading, Writing, and Rounding Whole Numbers...Ch. 1 - A. Reading, Writing, and Rounding Whole Numbers...Ch. 1 - Prob. 18APSCh. 1 - Prob. 19APSCh. 1 - Prob. 20APSCh. 1 - Prob. 21APSCh. 1 - Prob. 1BPSCh. 1 - Prob. 2BPSCh. 1 - Prob. 3BPSCh. 1 - Prob. 4BPSCh. 1 - Prob. 5BPSCh. 1 - Prob. 6BPSCh. 1 - Prob. 7BPSCh. 1 - Prob. 8BPSCh. 1 - Prob. 9BPSCh. 1 - Prob. 10BPSCh. 1 - Prob. 11BPSCh. 1 - Prob. 12BPSCh. 1 - Perform the arithmetic as shown. 734 85Ch. 1 - Prob. 14BPSCh. 1 - Prob. 15BPSCh. 1 - Prob. 16BPSCh. 1 - Perform the arithmetic as shown. 376 4Ch. 1 - Prob. 18BPSCh. 1 - Prob. 19BPSCh. 1 - Prob. 20BPSCh. 1 - B. Perform the arithmetic as shown. 207 63Ch. 1 - B. Perform the arithmetic as shown. 314 926Ch. 1 - Prob. 23BPSCh. 1 - Prob. 24BPSCh. 1 - Prob. 25BPSCh. 1 - Prob. 26BPSCh. 1 - B. Perform the arithmetic as shown. 422394Ch. 1 - Prob. 28BPSCh. 1 - Prob. 29BPSCh. 1 - Prob. 30BPSCh. 1 - Prob. 31BPSCh. 1 - Prob. 32BPSCh. 1 - B. Perform the arithmetic as shown. 36911342Ch. 1 - Prob. 34BPSCh. 1 - Prob. 35BPSCh. 1 - B. Perform the arithmetic as shown. 32 4 + 16 2 ...Ch. 1 - Prob. 37BPSCh. 1 - Prob. 38BPSCh. 1 - Prob. 39BPSCh. 1 - Prob. 40BPSCh. 1 - Prob. 41BPSCh. 1 - Prob. 42BPSCh. 1 - C. For each of the following whole numbers, (a)...Ch. 1 - C. For each of the following whole numbers, (a)...Ch. 1 - C. For each of the following whole numbers, (a)...Ch. 1 - C. For each of the following whole numbers, (a)...Ch. 1 - C. For each of the following whole numbers, (a)...Ch. 1 - C. For each of the following whole numbers, (a)...Ch. 1 - D. Practical Applications Electrical Trades From a...Ch. 1 - D. Practical Applications Machine Trades A machine...Ch. 1 - D. Practical Applications Construction Find the...Ch. 1 - D. Practical Applications Allied Health A patient...Ch. 1 - D. Practical Applications Electrical Trades...Ch. 1 - D. Practical Applications Flooring and Carpeting...Ch. 1 - D. Practical Applications Construction The weights...Ch. 1 - Prob. 8DPSCh. 1 - Prob. 9DPSCh. 1 - D. Practical Applications Electronics The output...Ch. 1 - Prob. 11DPSCh. 1 - Prob. 12DPSCh. 1 - D. Practical Applications Fire Protection A fire...Ch. 1 - D. Practical Applications Construction A pile of...Ch. 1 - D. Practical Applications Marine Technology If the...Ch. 1 - D. Practical Applications Automotive Trades A rule...Ch. 1 - D. Practical Applications Machine Trades If it...Ch. 1 - Prob. 18DPSCh. 1 - D. Practical Applications Manufacturing A gallon...Ch. 1 - D. Practical Applications Office Services The Ace...Ch. 1 - D. Practical Applications Manufacturing At 8 A.M....Ch. 1 - D. Practical Applications Fire Protection The...Ch. 1 - D. Practical Applications Carpentry A fireplace...Ch. 1 - D. Practical Applications Electronics When...Ch. 1 - D. Practical Applications Trades Management RAD...Ch. 1 - D. Practical Applications Life Skills An...Ch. 1 - D. Practical Applications Office Services Use the...Ch. 1 - D. Practical Applications Life Skills Gorilla glue...Ch. 1 - D. Practical Applications Automotive Trades A 2017...Ch. 1 - D. Practical Applications Landscaping A landscape...Ch. 1 - Prob. 31DPSCh. 1 - D. Practical Applications Construction A...Ch. 1 - Prob. 33DPSCh. 1 - D. Practical Applications Carpentry A set of eight...Ch. 1 - Agriculture A bushel of oats weighs 32 lb. How...Ch. 1 - Prob. 36DPSCh. 1 - D. Practical Applications HVAC In designing a...
Knowledge Booster
Background pattern image
Math
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
  • Text book image
    Intermediate Algebra
    Algebra
    ISBN:9781285195728
    Author:Jerome E. Kaufmann, Karen L. Schwitters
    Publisher:Cengage Learning
    Text book image
    Algebra for College Students
    Algebra
    ISBN:9781285195780
    Author:Jerome E. Kaufmann, Karen L. Schwitters
    Publisher:Cengage Learning
Text book image
Intermediate Algebra
Algebra
ISBN:9781285195728
Author:Jerome E. Kaufmann, Karen L. Schwitters
Publisher:Cengage Learning
Text book image
Algebra for College Students
Algebra
ISBN:9781285195780
Author:Jerome E. Kaufmann, Karen L. Schwitters
Publisher:Cengage Learning
SEE MORE TEXTBOOKS
Propositional Logic, Propositional Variables & Compound Propositions; Author: Neso Academy;https://www.youtube.com/watch?v=Ib5njCwNMdk;License: Standard YouTube License, CC-BY
Propositional Logic - Discrete math; Author: Charles Edeki - Math Computer Science Programming;https://www.youtube.com/watch?v=rL_8y2v1Guw;License: Standard YouTube License, CC-BY
DM-12-Propositional Logic-Basics; Author: GATEBOOK VIDEO LECTURES;https://www.youtube.com/watch?v=pzUBrJLIESU;License: Standard Youtube License
Lecture 1 - Propositional Logic; Author: nptelhrd;https://www.youtube.com/watch?v=xlUFkMKSB3Y;License: Standard YouTube License, CC-BY
MFCS unit-1 || Part:1 || JNTU || Well formed formula || propositional calculus || truth tables; Author: Learn with Smily;https://www.youtube.com/watch?v=XV15Q4mCcHc;License: Standard YouTube License, CC-BY