
Two bumper cars at the county fair are sliding toward one another (Fig. P11.54). Initially, bumper car 1 is traveling to the east at 5.62 m/s, and bumper car 2 is traveling 60.0° south of west at 10.00 m/s. After they collide, bumper car 1 is observed to be traveling to the west with a speed of 3.14 m/s. Friction is negligible between the cars and the ground. a. If the masses of bumper cars 1 and 2 are 596 kg and 625 kg respectively, what is the velocity of bumper car 2 immediately after the collision? b. What is the kinetic energy lost in the collision?
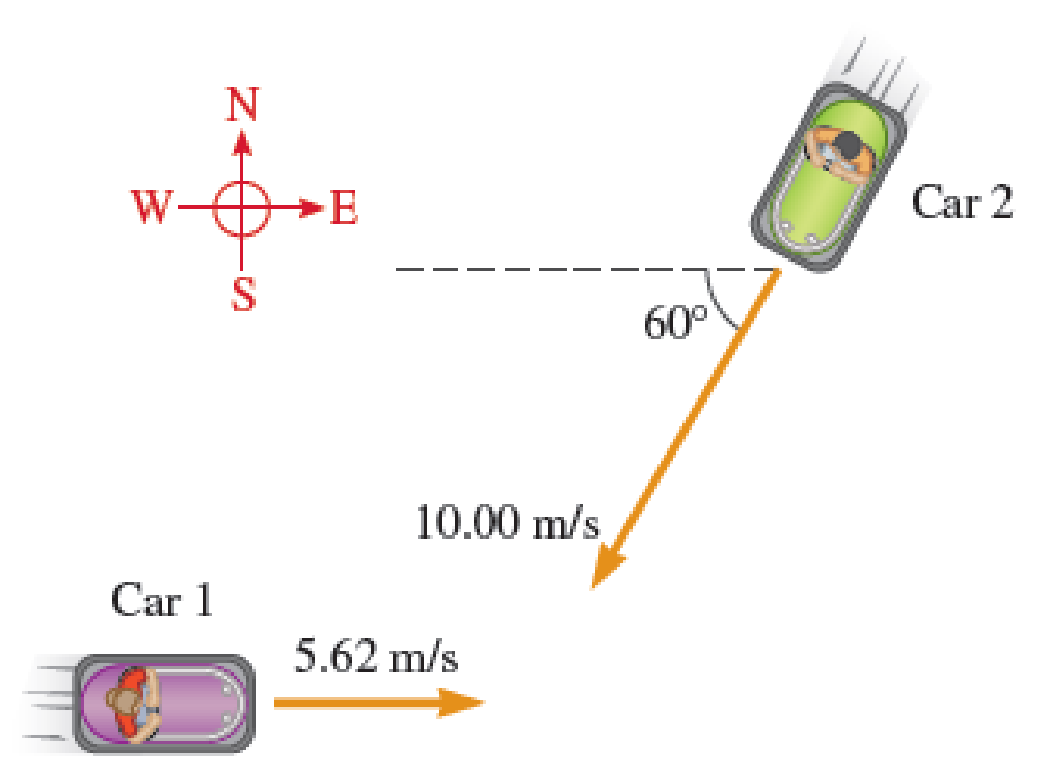
FIGURE P11.54 Problems 54 and 55.
(a)
Velocity of bumper car 2 after collision.
Answer to Problem 54PQ
Velocity of bumper car 2 after collision is
Explanation of Solution
Positive x axis points to the east and the positive y axis points to the north. Apply law of conservation of momentum. The momentum of cars before collision must be equal to the momentum of cars after collision.
Here,
Elaborate equation (I) in terms of mass and velocity.
Here,
Apply the same condition of conservation of momentum in the y direction also. Here only car 2 travels in the y direction.
The initial total momentum in the y direction is equal to the final momentum in the y direction.
Here,
Elaborate equation (III) in terms of mass and velocity.
Here,
Write the equation to find the final velocity of second car.
Here,
Conclusion:
Substitute
Substitute
Substitute
Therefore, velocity of bumper car 2 after collision is
(b)
Kinetic energy lost during the collision.
Answer to Problem 54PQ
The kinetic energy lost is
Explanation of Solution
Write the equation to find the resultant final speed of car 2 after collision.
Here,
The kinetic energy lost is equal to the difference between the kinetic energy before collision and after collision.
Write the equation to find the kinetic energy lost.
Here,
Conclusion:
Substitute
Substitute
Therefore, the kinetic energy lost is
Want to see more full solutions like this?
Chapter 11 Solutions
Webassign Printed Access Card For Katz's Physics For Scientists And Engineers: Foundations And Connections, 1st Edition, Single-term
- please help me solve this questions. show all calculations and a good graph too :)arrow_forwardWhat is the force (in N) on the 2.0 μC charge placed at the center of the square shown below? (Express your answer in vector form.) 5.0 με 4.0 με 2.0 με + 1.0 m 1.0 m -40 με 2.0 μCarrow_forwardWhat is the force (in N) on the 5.4 µC charge shown below? (Express your answer in vector form.) −3.1 µC5.4 µC9.2 µC6.4 µCarrow_forward
- An ideal gas in a sealed container starts out at a pressure of 8900 N/m2 and a volume of 5.7 m3. If the gas expands to a volume of 6.3 m3 while the pressure is held constant (still at 8900 N/m2), how much work is done by the gas? Give your answer as the number of Joules.arrow_forwardThe outside temperature is 25 °C. A heat engine operates in the environment (Tc = 25 °C) at 50% efficiency. How hot does it need to get the high temperature up to in Celsius?arrow_forwardGas is compressed in a cylinder creating 31 Joules of work on the gas during the isothermal process. How much heat flows from the gas into the cylinder in Joules?arrow_forward
- The heat engine gives 1100 Joules of energy of high temperature from the burning gasoline by exhausting 750 Joules to low-temperature . What is the efficiency of this heat engine in a percentage?arrow_forwardL₁ D₁ L₂ D2 Aluminum has a resistivity of p = 2.65 × 10 8 2. m. An aluminum wire is L = 2.00 m long and has a circular cross section that is not constant. The diameter of the wire is D₁ = 0.17 mm for a length of L₁ = 0.500 m and a diameter of D2 = 0.24 mm for the rest of the length. a) What is the resistance of this wire? R = Hint A potential difference of AV = 1.40 V is applied across the wire. b) What is the magnitude of the current density in the thin part of the wire? Hint J1 = c) What is the magnitude of the current density in the thick part of the wire? J₂ = d) What is the magnitude of the electric field in the thin part of the wire? E1 = Hint e) What is the magnitude of the electric field in the thick part of the wire? E2 =arrow_forwardplease helparrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





