EXCURSIONS IN MOD.MATH W/ACCESS >BI<
9th Edition
ISBN: 9781323788721
Author: Tannenbaum
Publisher: PEARSON C
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 11, Problem 32E
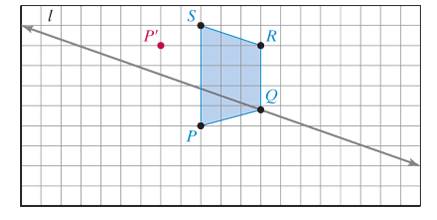
In Fig 11-63,
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Let R be field and X= R³/s Vector space over R
M=(a,b,c)labic, e Rra+b= 3- <3
Show that Ms and why with proof.
1) is convexset and affine set of botost
ii) is blanced set and symmetirs set of x
iii) is hy per space and hyper plane ofx or hot
iii) find f:MR st kerf = M 18/103
and finnd fiM→R/{0} st
M= {xEX, f(t) = x, texiαER?
jiii) show that Mis Maxsubspace or not
and Mis a max. affine set or not.
Solve the next ED: (see image)
Write an equation for the polynomial graphed below. It will probably be easiest to leave your "a" value as a
fraction.
8
7
+
9+
H
6
5
4
3
+ 3
2
1
(-30)
(-1,0)
(1,0)
(3,0)
+
-5
-4
-3
-2
2
3
4
7 2
-1
-2
3 (0,-3)
f(x) =
456
-4
-5
-6+
Chapter 11 Solutions
EXCURSIONS IN MOD.MATH W/ACCESS >BI<
Ch. 11 - In Fig.1135_, indicate which point is the image of...Ch. 11 - Prob. 2ECh. 11 - Prob. 3ECh. 11 - In Fig. 11-38, P is the image of P under a...Ch. 11 - In Fig.11-39, l is the axis of reflection. a.Find...Ch. 11 - In Fig. 11-40, l is the axis of reflection. a....Ch. 11 - Prob. 7ECh. 11 - In Fig 11-42, P is the image of P under a...Ch. 11 - In Fig. 11-43, P is image of P under a reflection....Ch. 11 - Prob. 10E
Ch. 11 - In Fig. 11-45, A and B are fixed points of a...Ch. 11 - Prob. 12ECh. 11 - In Fig. 11-47, indicate which point is a. the...Ch. 11 - Prob. 14ECh. 11 - In each case, give an answer between 0 and 360. 1....Ch. 11 - Prob. 16ECh. 11 - Prob. 17ECh. 11 - Prob. 18ECh. 11 - Prob. 19ECh. 11 - Prob. 20ECh. 11 - Prob. 21ECh. 11 - Prob. 22ECh. 11 - In Fig. 11-54, indicate which point is the image...Ch. 11 - Prob. 24ECh. 11 - Prob. 25ECh. 11 - In Fig. 11-57, Q is the image of Q under a...Ch. 11 - In Fig. 11-58, D is the image of D under a...Ch. 11 - Prob. 28ECh. 11 - Prob. 29ECh. 11 - Prob. 30ECh. 11 - Prob. 31ECh. 11 - In Fig 11-63, P is the image of P under a glide...Ch. 11 - In Fig.11-64, B is the image of B and D is the...Ch. 11 - Prob. 34ECh. 11 - Prob. 35ECh. 11 - Prob. 36ECh. 11 - In Fig 11-68, D is the image of D and C is the...Ch. 11 - In Fig11-69, A is the image of A and D is the...Ch. 11 - Prob. 39ECh. 11 - Prob. 40ECh. 11 - Prob. 41ECh. 11 - Prob. 42ECh. 11 - Prob. 43ECh. 11 - Prob. 44ECh. 11 - Prob. 45ECh. 11 - Prob. 46ECh. 11 - Find the symmetry type for each of the following...Ch. 11 - Prob. 48ECh. 11 - Prob. 49ECh. 11 - Prob. 50ECh. 11 - Prob. 51ECh. 11 - Prob. 52ECh. 11 - Prob. 53ECh. 11 - Prob. 54ECh. 11 - Prob. 55ECh. 11 - Prob. 56ECh. 11 - Prob. 57ECh. 11 - Prob. 58ECh. 11 - Prob. 59ECh. 11 - Prob. 60ECh. 11 - Prob. 61ECh. 11 - Prob. 62ECh. 11 - Prob. 63ECh. 11 - Prob. 64ECh. 11 - Suppose that a rigid motion M is the product of a...Ch. 11 - Prob. 66ECh. 11 - Prob. 67ECh. 11 - Prob. 68ECh. 11 - Prob. 69ECh. 11 - Prob. 70ECh. 11 - Prob. 71ECh. 11 - Prob. 72ECh. 11 - Prob. 73ECh. 11 - Prob. 74ECh. 11 - Prob. 75ECh. 11 - Prob. 76ECh. 11 - Prob. 77ECh. 11 - Prob. 78ECh. 11 - Prob. 79ECh. 11 - Prob. 80E
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Write an equation for the polynomial graphed below 5+ 4 - 3 2 1 + + -5 4-3 -2 -1 1 2 3 4 5 -1 -2 y(x) = -3 -4 5 -5+ Qarrow_forwardWrite an equation for the polynomial graphed below 6+ 5 + -5 -4 3 y(x) = 4 3 2 1 -1 1 1 -1 -2 -3 -4 -5 2 3 4 5arrow_forwardWrite an equation for the polynomial graphed below 5+ 4 3 1 + + + -5-4-3-2 1 13 4 5 -1 -2 -3 -4 -5+ 4 5 Q y(x) =arrow_forward
- 1. Name the ongiewing) 2. Name five pairs of supple 3 27 and 19 form a angles 210 and 21 are complementary angies 4. m210=32 mal!= 5 mc11-72 m10= 6 m210-4x mc11=2x x= 7 m210=x m 11 =x+20; x= 12 and 213 are supplementary angles 8 ma 12 2y m13-3y-15 y= 9 m 12-y+10 m13-3y+ 10: y= 10. The measure of 212 is five times the measure of 13. Find the 213 and 214 are complementary angles, and 14 and 15 are supplementary angies 11 mc13 47 m/14- 12 m 14-78 m13- m215- m15 13 m15-135 m. 13- m.14arrow_forward3. Solve the inequality, and give your answer in interval notation. - (x − 4)³ (x + 1) ≥ 0arrow_forward1. Find the formula to the polynomial at right. Show all your work. (4 points) 1- 2 3 сл 5 6 -4 -3 -2 -1 0 2 3arrow_forward
- 2. Find the leading term (2 points): f(x) = −3x(2x − 1)²(x+3)³ -arrow_forward1- √ √ √³ e³/√xdy dx 1 cy² 2- √ √² 3 y³ exy dx dy So 3- √ √sinx y dy dx 4- Jo √² Sy² dx dyarrow_forwardA building that is 205 feet tall casts a shadow of various lengths æ as the day goes by. An angle of elevation is formed by lines from the top and bottom of the building to the tip of the shadow, as de seen in the following figure. Find the rate of change of the angle of elevation when x 278 feet. dx Round to 3 decimal places. Γ X radians per footarrow_forward
- Find The partial fraction decomposition for each The following 2× B) (x+3) a 3 6 X-3x+2x-6arrow_forward1) Find the partial feraction decomposition for each of 5- X 2 2x+x-1 The following: 3 B) 3 X + 3xarrow_forwardUse the information in the following table to find h' (a) at the given value for a. x|f(x) g(x) f'(x) g(x) 0 0 0 4 3 1 4 4 3 0 2 7 1 2 7 3 3 1 2 9 4 0 4 5 7 h(x) = f(g(x)); a = 0 h' (0) =arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:9781305658004
Author:Ron Larson
Publisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning
HOW TO FIND DETERMINANT OF 2X2 & 3X3 MATRICES?/MATRICES AND DETERMINANTS CLASS XII 12 CBSE; Author: Neha Agrawal Mathematically Inclined;https://www.youtube.com/watch?v=bnaKGsLYJvQ;License: Standard YouTube License, CC-BY
What are Determinants? Mathematics; Author: Edmerls;https://www.youtube.com/watch?v=v4_dxD4jpgM;License: Standard YouTube License, CC-BY