Calculus: Early Transcendentals, Enhanced Etext
Calculus: Early Transcendentals, Enhanced Etext
12th Edition
ISBN: 9781119777984
Author: Howard Anton; Irl C. Bivens; Stephen Davis
Publisher: Wiley Global Education US
bartleby

Concept explainers

Limits
When it comes to calculus, limits are considered to be a very important topic of discussion. The main importance of limit lies in expressing the value of a function as it gets closer to a certain value. Also, limits can help you to understand other topic…
bartleby

Videos

Textbook Question
Book Icon
Chapter 1.1, Problem 31ES

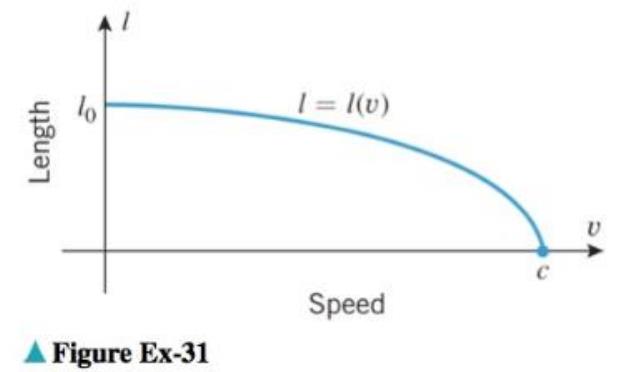
In the special theory of relativity the length l of a narrow rod moving longitudinally is a function l = l υ of the rod’s speed υ . The accompanying figure, in which c denotes the speed of light, displays some of the qualitative features of this function.

(a) What is the physical interpretation of l 0 ?

(b) What is lim υ → c − l υ ? What is the physical significance of this limit?

Chapter 1.1, Problem 31ES, In the special theory of relativity the length l of a narrow rod moving longitudinally is a function

Expert Solution & Answer
Check Mark

Want to see the full answer?

Check out a sample textbook solution
Blurred answer
Previous
Chapter 1.1, Problem 30ES
Next
Chapter 1.1, Problem 32ES
Students have asked these similar questions
Which of the following shows a graph of a tangent function in the form y = atan(bx - c)+d, such that b = 2?
Starting at point (1,0), you move along a distance t along a unit circle until you reach a terminal point at P(1213,513)P(1213,513). Find all six trignometric functions of t. Express your answer as a reduced fraction, NO DECIMALS!
pls help asap. pls only use advanced functions grade 12 methods and not use any calculus while showing steps.

Chapter 1 Solutions

Calculus: Early Transcendentals, Enhanced Etext

Ch. 1.1 - We write limxafx=L provided the values of can be...Ch. 1.1 - We write limxafx=+ provided increases without...Ch. 1.1 - State what must be true about limxafxandlimxa+fx...Ch. 1.1 - The slope of the secant line through P2,4 and...Ch. 1.1 - Use the accompanying graph of y=fxx3 to determine...Ch. 1.1 - In these exercises, make reasonable assumptions...Ch. 1.1 - In these exercises, make reasonable assumptions...Ch. 1.1 - In these exercises, make reasonable assumptions...Ch. 1.1 - In these exercises, make reasonable assumptions...Ch. 1.1 - Prob. 5ES
Ch. 1.1 - In these exercises, make reasonable assumptions...Ch. 1.1 - In these exercises, make reasonable assumptions...Ch. 1.1 - In these exercises, make reasonable assumptions...Ch. 1.1 - In these exercises, make reasonable assumptions...Ch. 1.1 - In these exercises, make reasonable assumptions...Ch. 1.1 - (i) Complete the table and make a guess about the...Ch. 1.1 - (i) Complete the table and make a guess about the...Ch. 1.1 - (i) Make a guess at the limit (if it exists) by...Ch. 1.1 - (i) Make a guess at the limit (if it exists) by...Ch. 1.1 - Prob. 16ESCh. 1.1 - Determine whether the statement is true or false....Ch. 1.1 - True-False Determine whether the statement is true...Ch. 1.1 - True-False Determine whether the statement is true...Ch. 1.1 - Prob. 20ESCh. 1.1 - Sketch a possible graph for a function f with the...Ch. 1.1 - Sketch a possible graph for a function f with the...Ch. 1.1 - Sketch a possible graph for a function f with the...Ch. 1.1 - Prob. 25ESCh. 1.1 - Sketch a possible graph for a function f with the...Ch. 1.1 - Modify he argument of Example 1 to find the...Ch. 1.1 - Modify he argument of Example 1 to find the...Ch. 1.1 - Modify he argument of Example 1 to find the...Ch. 1.1 - Modify he argument of Example 1 to find the...Ch. 1.1 - In the special theory of relativity the length l...Ch. 1.1 - In the special theory of relativity the mass m of...Ch. 1.1 - Two students are discussing the limit of x as x...Ch. 1.1 - Given a function f and a real number a , explain...Ch. 1.2 - In each part, find the limit by inspection. (a)...Ch. 1.2 - Given that limxafx=1 and limxagx=2 , find the...Ch. 1.2 - Find the limits. (a) limx1x3+x2+x101= (b)...Ch. 1.2 - Let fx=x+1,x1x1,x1 Find the limits that exist. (a)...Ch. 1.2 - Given that limxafx=2,limxagx=4,limxahx=0 find the...Ch. 1.2 - Use the graph of f and g in the accompanying...Ch. 1.2 - Find the limits. limx2xx1x+1Ch. 1.2 - Prob. 4ESCh. 1.2 - Find the limits. limx3x22xx+1Ch. 1.2 - Find the limits. limx06x9x312x+3Ch. 1.2 - Find the limits. limx1+x41x1Ch. 1.2 - Find the limits. limt2t3+8t+2Ch. 1.2 - Find the limits. limx1x2+6x+5x23x4Ch. 1.2 - Find the limits. limx2x24x+4x2+x6Ch. 1.2 - Prob. 11ESCh. 1.2 - Find the limits. limx13x2x22x2+x3Ch. 1.2 - Find the limits. limt2t3+3t212t+4t34tCh. 1.2 - Find the limits. limt1t3+t25t+3t33t+2Ch. 1.2 - Find the limits. limx3+xx3Ch. 1.2 - Find the limits. limx3xx3Ch. 1.2 - Find the limits. limx3xx3Ch. 1.2 - Find the limits. limx2+xx24Ch. 1.2 - Find the limits. limx2xx24Ch. 1.2 - Find the limits. limx2xx24Ch. 1.2 - Find the limits. limy6+y+6y236Ch. 1.2 - Find the limits. limy6y+6y236Ch. 1.2 - Find the limits. limy6y+6y236Ch. 1.2 - Find the limits. limx4+3xx22x8Ch. 1.2 - Find the limits. limx43xx22x8Ch. 1.2 - Find the limits. limx43xx22x8Ch. 1.2 - Find the limits. limx2+12xCh. 1.2 - Find the limits. limx31x3Ch. 1.2 - Find the limits. limx9x9x3Ch. 1.2 - Prob. 30ESCh. 1.2 - Let fx=x1,x33x7,x3 Find (a) limx3fx (b) limx3+fx...Ch. 1.2 - Let gt=t2,t0t2,0t22t,t2 Find (a) limt0gt (b)...Ch. 1.2 - True-False Determine whether the statement is true...Ch. 1.2 - True-False Determine whether the statement is true...Ch. 1.2 - True-False Determine whether the statement is true...Ch. 1.2 - True-False Determine whether the statement is true...Ch. 1.2 - First rationalize the numerator and then find the...Ch. 1.2 - First rationalize the numerator and then find the...Ch. 1.2 - Let fx=x31x1 (a) Find limx1fx . (b) Sketch the...Ch. 1.2 - (a) Explain why the following calculation is...Ch. 1.2 - Prob. 42ESCh. 1.2 - Find all value of a such that limx11x1ax21 exists...Ch. 1.2 - (a) Explain informally why limx01x+1x2=+ (b)...Ch. 1.2 - Let px and qx be polynomials, with qx0=0 . Discuss...Ch. 1.2 - Suppose that f and g are two functions such that...Ch. 1.2 - Suppose that f and g are two functions such that...Ch. 1.2 - Suppose that f and g are two functions such that...Ch. 1.3 - Find the limits. (a) limx+2x= (b) limxxx= (c)...Ch. 1.3 - Find the limits that exist. (a) limx2x2+x4x23= (b)...Ch. 1.3 - Given that limx+fx=2andlimx+gx=3 Find the limits...Ch. 1.3 - Consider the graph of y=1/x+1,y=x/x+1, and...Ch. 1.3 - In these exercises, make reasonable assumptions...Ch. 1.3 - In these exercises, make reasonable assumptions...Ch. 1.3 - In these exercises, make reasonable assumptions...Ch. 1.3 - In these exercises, make reasonable assumptions...Ch. 1.3 - Given that limx+fx=3,limx+gx=5,limx+hx=0 find the...Ch. 1.3 - Complete the table and make a guess about the...Ch. 1.3 - Complete the table and make a guess about the...Ch. 1.3 - Prob. 9ESCh. 1.3 - Find the limits. limx+2x3100x+5Ch. 1.3 - Find the limits. limx+xCh. 1.3 - Prob. 12ESCh. 1.3 - Find the limits. limx+3x+12x5Ch. 1.3 - Find the limits. limx+5x24x2x2+3Ch. 1.3 - Find the limits. limy3y+4Ch. 1.3 - Find the limits. limx+1x12Ch. 1.3 - Find the limits. limxx2x2+2x+1Ch. 1.3 - Prob. 18ESCh. 1.3 - Find the limits. limx+76x5x+3Ch. 1.3 - Find the limits. limt52t3t2+1Ch. 1.3 - Find the limits. limt+6t37t3+3Ch. 1.3 - Prob. 22ESCh. 1.3 - Find the limits. limx+2+3x5x21+8x23Ch. 1.3 - Find the limits. lims+3s74s52s7+13Ch. 1.3 - Find the limits. limx5x22x+3Ch. 1.3 - Find the limits. limx+5x22x+3Ch. 1.3 - Find the limits. limy2y7+6y2Ch. 1.3 - Find the limits. limy+2y7+6y2Ch. 1.3 - Find the limits. limx3x4+xx28Ch. 1.3 - Find the limits. limx+3x4+xx28Ch. 1.3 - Find the limits. limx+x2+3xCh. 1.3 - Find the limits. limx+x23xxCh. 1.3 - Determine whether the statement is true or false....Ch. 1.3 - Prob. 34ESCh. 1.3 - Determine whether the statement is true or false....Ch. 1.3 - Determine whether the statement is true or false....Ch. 1.3 - Let T=ft denote the temperature of a baked potato...Ch. 1.3 - Let fx=2x2+5,x035x31+4x+x3,x0 Find (a) limxgx (b)...Ch. 1.3 - Let...Ch. 1.3 - Discuss the limits of px=1xn as x+ and x for...Ch. 1.3 - In each part, find examples of polynomials px and...Ch. 1.3 - (a) Do any of the trigonometric functions sinx,...Ch. 1.3 - Find limx+c0+c1x++cnxnd0+d1x++dmxm where cn0 and...Ch. 1.3 - These exercises develop some versions of the...Ch. 1.3 - These exercises develop some versions of the...Ch. 1.3 - Given that limxfx=0 and limx+fx=+ evaluate the...Ch. 1.3 - Given that limxfx=0 and limx+fx=+ evaluate the...Ch. 1.3 - Given that limxfx=0 and limx+fx=+ evaluate the...Ch. 1.3 - Given that limxfx=0 and limx+fx=+ evaluate the...Ch. 1.3 - The notion of an asymptote can be extended to...Ch. 1.3 - The notion of an asymptote can be extended to...Ch. 1.3 - The notion of an asymptote can be extended to...Ch. 1.4 - The definition of a two-sided limit states:...Ch. 1.4 - Suppose that fx is a function such that for any...Ch. 1.4 - Suppose that is any positive number. Find the...Ch. 1.4 - The definition of limit at + states: limx+fx=L if...Ch. 1.4 - Find the smallest positive number N such that for...Ch. 1.4 - (a) Find the largest open interval, centered at...Ch. 1.4 - Prob. 2ESCh. 1.4 - (a) Find the values of x0 and x1 in the...Ch. 1.4 - (a) Find the values of x0 and x1 in the...Ch. 1.4 - Generate the graph of fx=x34x+5 with a graphing...Ch. 1.4 - Let fx=sin2x/x and use a graphing utility to...Ch. 1.4 - Prob. 9ESCh. 1.4 - A positive number and the limit L of a function f...Ch. 1.4 - Prob. 11ESCh. 1.4 - Prob. 12ESCh. 1.4 - A positive number and the limit L of a function f...Ch. 1.4 - Prob. 14ESCh. 1.4 - Prob. 15ESCh. 1.4 - Prob. 16ESCh. 1.4 - Prob. 17ESCh. 1.4 - Prob. 18ESCh. 1.4 - Use Definition 1.4.1 to prove that the limit is...Ch. 1.4 - Prob. 20ESCh. 1.4 - Prob. 21ESCh. 1.4 - Use Definition 1.4.1 to prove that the limit is...Ch. 1.4 - Use Definition 1.4.1 to prove that the limit is...Ch. 1.4 - Use Definition 1.4.1 to prove that the limit is...Ch. 1.4 - Use Definition 1.4.1 to prove that the limit is...Ch. 1.4 - Prob. 26ESCh. 1.4 - Given rigorous definitions of limxa+fx=L and...Ch. 1.4 - Consider the statement that limxafxL=0 . (a) Using...Ch. 1.4 - (a) Show that 3x2+2x20300=3x+32x10 (b) Find an...Ch. 1.4 - (a) Show that 283x+14=123x+1x2 (b) Is 123x+1...Ch. 1.4 - Use Definition 1.4.1 to prove that the stated...Ch. 1.4 - Use Definition 1.4.1 to prove that the stated...Ch. 1.4 - Prob. 34ESCh. 1.4 - Use Definition 1.4.1 to prove that the stated...Ch. 1.4 - Use Definition 1.4.1 to prove that the stated...Ch. 1.4 - Let fx0,ifxisrationalx,ifxisirrational Use...Ch. 1.4 - Let fx0,ifxisrational1,ifxisirrational Use...Ch. 1.4 - (a) Find the smallest positive number N such that...Ch. 1.4 - In each part, find the smallest positive value of...Ch. 1.4 - (a) Find the values of x1 and x2 in the...Ch. 1.4 - (a) Find the values of x1 and x2 in the...Ch. 1.4 - A positive number and the limit L of a function f...Ch. 1.4 - A positive number and the limit L of a function f...Ch. 1.4 - A positive number and the limit L of a function f...Ch. 1.4 - A positive number and the limit L of a function f...Ch. 1.4 - A positive number and the limit L of a function f...Ch. 1.4 - A positive number and the limit L of a function f...Ch. 1.4 - A positive number and the limit L of a function f...Ch. 1.4 - Prob. 50ESCh. 1.4 - Use Definition 1.4.2 or 1.4.3 to prove that the...Ch. 1.4 - Use Definition 1.4.2 or 1.4.3 to prove that the...Ch. 1.4 - Use Definition 1.4.2 or 1.4.3 to prove that the...Ch. 1.4 - Use Definition 1.4.2 or 1.4.3 to prove that the...Ch. 1.4 - Use Definition 1.4.2 or 1.4.3 to prove that the...Ch. 1.4 - (a) Find the largest open interval, centered at...Ch. 1.4 - In each part, find the largest open interval...Ch. 1.4 - Use Definition 1.4.4 or 1.4.5 to prove that the...Ch. 1.4 - Use Definition 1.4.4 or 1.4.5 to prove that the...Ch. 1.4 - Use Definition 1.4.4 or 1.4.5 to prove that the...Ch. 1.4 - Use Definition 1.4.4 or 1.4.5 to prove that the...Ch. 1.4 - Use Definition 1.4.4 or 1.4.5 to prove that the...Ch. 1.4 - Use Definition 1.4.4 or 1.4.5 to prove that the...Ch. 1.4 - Use the definitions in Exercise 27 to prove that...Ch. 1.4 - Use the definitions in Exercise 27 to prove that...Ch. 1.4 - Use the definitions in Exercise 27 to prove that...Ch. 1.4 - Use the definitions in Exercise 27 to prove that...Ch. 1.4 - Write out the definition for the corresponding...Ch. 1.4 - Write out the definition for the corresponding...Ch. 1.4 - Write out the definition for the corresponding...Ch. 1.4 - Write out the definition for the corresponding...Ch. 1.4 - According to Ohm’s law, when a voltage of V...Ch. 1.5 - What three conditions are satisfied if f is...Ch. 1.5 - Suppose that f and g are continuous functions such...Ch. 1.5 - Suppose that f and g are continuous functions such...Ch. 1.5 - For what values of x, if any, is the function...Ch. 1.5 - Suppose that function f is continuous everywhere...Ch. 1.5 - Let f be the function whose graph is shown. On...Ch. 1.5 - 1-4 Let f be the function whose graph is shown. On...Ch. 1.5 - Consider the functions fx=1,0x0,x0 and gx=0,0x1,x0...Ch. 1.5 - In each part sketch the graph of a function f that...Ch. 1.5 - The accompanying figure models the concentration C...Ch. 1.5 - A student parking lot at a university charges...Ch. 1.5 - In each part determine whether the function is...Ch. 1.5 - Prob. 11ESCh. 1.5 - Find values of x, if any, at which f is not...Ch. 1.5 - Find values of x, if any, at which f is not...Ch. 1.5 - Find values of x, if any, at which f is not...Ch. 1.5 - Find values of x, if any, at which f is not...Ch. 1.5 - Find values of x, if any, at which f is not...Ch. 1.5 - Find values of x, if any, at which f is not...Ch. 1.5 - Prob. 18ESCh. 1.5 - Find values of x, if any, at which f is not...Ch. 1.5 - Find values of x, if any, at which f is not...Ch. 1.5 - Find values of x, if any, at which f is not...Ch. 1.5 - Determine whether the statement is true or false....Ch. 1.5 - Determine whether the statement is true or false....Ch. 1.5 - Determine whether the statement is true or false....Ch. 1.5 - Determine whether the statement is true or false....Ch. 1.5 - Determine whether the statement is true or false....Ch. 1.5 - Determine whether the statement is true or false....Ch. 1.5 - Find a value of the constant k, if possible, that...Ch. 1.5 - Find values of the constants k and m, if possible,...Ch. 1.5 - A function is said to have a removable...Ch. 1.5 - A function f is said to have a removable...Ch. 1.5 - A function is said to have a removable...Ch. 1.5 - (a) Use a graphing utility to generate the graph...Ch. 1.5 - (a) Use a graphing utility to generate the graph...Ch. 1.5 - Prove that fx=x3/5 is continuous everywhere,...Ch. 1.5 - Prove that is continuous everywhere, carefully...Ch. 1.5 - Prove: (a) Part a of Theorem 1.5.3 (b) Part b of...Ch. 1.5 - Prove part of Theorem . Ch. 1.5 - (a) Use Theorem 1.5.5 to prove that if f is...Ch. 1.5 - Prove: If f and g are continuous on a,b, and...Ch. 1.5 - Give an example of a function that is defined on...Ch. 1.5 - Let f be the function whose graph is shown in...Ch. 1.5 - Show that the equation x3+x22x=1 has at least one...Ch. 1.5 - Prove: If is a polynomial of odd degree, then the...Ch. 1.5 - The accompanying figure on the next page shows...Ch. 1.5 - The accompanying figure shows that graph of the...Ch. 1.5 - A sprinter, who is timed with a stopwatch, runs a...Ch. 1.5 - Prove that there exist points on opposite sides of...Ch. 1.5 - Let R denote an elliptical region in the xy-plane,...Ch. 1.5 - Let R denote an elliptical region in the plane....Ch. 1.5 - Suppose that f is continuous on the interval 0,1...Ch. 1.5 - Suppose that f is an invertible function, f0=0,f...Ch. 1.6 - In each part, is the given function continuous on...Ch. 1.6 - Evaluate (a) limx0sinxx (b) limx01cosxx .Ch. 1.6 - Suppose a function f has the property that for all...Ch. 1.6 - Find the discontinuities, if any. fx=sinx22Ch. 1.6 - Find the discontinuities, if any. fx=cotxCh. 1.6 - Find the discontinuities, if any. fx=secxCh. 1.6 - Prob. 5ESCh. 1.6 - Find the discontinuities, if any. fx=11+sin2xCh. 1.6 - Find the discontinuities, if any. fx=112sinxCh. 1.6 - Find the discontinuities, if any. fx=2+tan2xCh. 1.6 - In each part, use Theorem 1.5.6b to show that the...Ch. 1.6 - Prob. 11ESCh. 1.6 - Prob. 12ESCh. 1.6 - Prob. 13ESCh. 1.6 - Find the limits. limh0sinh2hCh. 1.6 - Prob. 15ESCh. 1.6 - Prob. 16ESCh. 1.6 - Find the limits. lim0+sin2Ch. 1.6 - Prob. 18ESCh. 1.6 - Find the limits. limx0tan7xsin3xCh. 1.6 - Find the limits. limx0sin6xsin8xCh. 1.6 - Prob. 21ESCh. 1.6 - Find the limits. limx0sin2x3x2Ch. 1.6 - Find the limits. 23. limx01cos3x+sin4x5xCh. 1.6 - Find the limits. limh0sinh1coshCh. 1.6 - Find the limits. limt0t21cos2tCh. 1.6 - Find the limits. limx0xcos12xCh. 1.6 - Prob. 27ESCh. 1.6 - Find the limits. limh01cos3hcos25h1Ch. 1.6 - Prob. 29ESCh. 1.6 - Prob. 30ESCh. 1.6 - Find the limits. limx0tanaxsinbx,a0,b0Ch. 1.6 - Prob. 32ESCh. 1.6 - Prob. 33ESCh. 1.6 - (a) Complete the table and make a guess about the...Ch. 1.6 - True-False Determine whether the statement is true...Ch. 1.6 - Determine whether the statement is true or false....Ch. 1.6 - Determine whether the statement is true or false....Ch. 1.6 - Determine whether the statement is true or false....Ch. 1.6 - In an attempt to verify that limx0sinx/x=1 , a...Ch. 1.6 - In the circle in the accompanying figure, a...Ch. 1.6 - Find a nonzero value for the constant k that makes...Ch. 1.6 - Is fx=sinxx,x01,x=0 continuous at x=0 ? Explain.Ch. 1.6 - In parts (a)-(c), find the limit by making the...Ch. 1.6 - Find limx2cos/xx2 .Ch. 1.6 - Prob. 45ESCh. 1.6 - Find limx/4tanx1x/4 .Ch. 1.6 - Use the Squeezing Theorem to show that...Ch. 1.6 - Use the Squeezing Theorem to show that...Ch. 1.6 - In Example 3 we used the Squeezing Theorem to...Ch. 1.6 - Prob. 50ESCh. 1.6 - Sketch the graphs of the curves y=1/x,y=1/x, and...Ch. 1.6 - Prob. 52ESCh. 1.6 - (a) Use the Intermediate-Value Theorem to show...Ch. 1.6 - In the study of falling objects near the surface...Ch. 1.7 - Prob. 1QCECh. 1.7 - Prob. 2QCECh. 1.7 - In each part, determine the exact value without...Ch. 1.7 - In each part, determine the exact value without...Ch. 1.7 - Determine where f is continuous. fx=sin12xCh. 1.7 - Determine where f is continuous. fx=tan1xx29Ch. 1.7 - Determine where f is continuous. fx=sin11/xxCh. 1.7 - Given that =tan143, find the exact values of...Ch. 1.7 - Given that =sec12.6, find the exact values of...Ch. 1.7 - For which values of is it true that (a) (b)...Ch. 1.7 - Find the exact value of the given quantity....Ch. 1.7 - Find the exact value of the given quantity....Ch. 1.7 - Complete the identities using the triangle method...Ch. 1.7 - Complete the identities using the triangle method...Ch. 1.7 - (a) Use a calculating utility set to radian...Ch. 1.7 - The law of cosines states that c2=a2+b22abcos...Ch. 1.7 - Prob. 15ESCh. 1.7 - Use a calculating utility to approximate the...Ch. 1.7 - (a) Use a calculating utility to evaluate the...Ch. 1.7 - A soccer player kicks a ball with an initial speed...Ch. 1.7 - Prob. 19ESCh. 1.7 - Find the limits. 20. limxn+tan1(cscx)Ch. 1.7 - Determine whether the statement is true or false....Ch. 1.7 - Determine whether the statement is true or false....Ch. 1.7 - Determine whether the statement is true or false....Ch. 1.7 - Prob. 24ESCh. 1.7 - Prob. 25ESCh. 1.7 - From Exercise 1.5.58, under the assumptions that f...Ch. 1.7 - Prob. 27ESCh. 1.7 - Prob. 28ESCh. 1.7 - The function cot1x is defined to be the inverse of...Ch. 1.7 - The function cot1x is defined to be the inverse of...Ch. 1.7 - Most scientific calculators have keys for the...Ch. 1.7 - A camera is positioned x feet from the base of a...Ch. 1.7 - The number of hours of daylight on a given day at...Ch. 1.7 - An Earth-observing satellite has horizon sensors...Ch. 1.7 - An airplane is flying at a constant height of...Ch. 1.7 - Prove: (a) sin1x=sin1x (b) tan1x=tan1x .Ch. 1.7 - Prove: (a) cos1x=cos1x (b) sec1x=sec1x .Ch. 1.7 - Prove: (a) sin1x=tan1x1x2x1 (b) cos1x=2tan1x1x2x1...Ch. 1.7 - Prove: tan1x+tan1y=tan1x+y1xy provided...Ch. 1.7 - Use the result in Exercise 39 to show that (a)...Ch. 1.7 - Use identities 7 and 10 to obtain identity 14 .Ch. 1.7 - Writing Let =tan13/4 and explain why the triangle...Ch. 1.8 - The function y=12x has domain and range .Ch. 1.8 - The function has domain and range . Ch. 1.8 - Express as a power of 4 : (a) 1 (b) 2 (c) 116 (d)...Ch. 1.8 - Solve each equation for x . (a) ex=12 (b)...Ch. 1.8 - Solve each equation for x . (a) lnx=3 (b) logx1=2...Ch. 1.8 - Simplify the expression without using a...Ch. 1.8 - Simplify the expression without using a...Ch. 1.8 - Use a calculating utility to approximate the...Ch. 1.8 - Prob. 4ESCh. 1.8 - Find the exact value of the expression without...Ch. 1.8 - Prob. 6ESCh. 1.8 - Use a calculating utility to approximate the...Ch. 1.8 - Prob. 8ESCh. 1.8 - Use the logarithm properties in Theorem 1.8.3 to...Ch. 1.8 - Prob. 10ESCh. 1.8 - Expand the logarithm in terms of sums,...Ch. 1.8 - Prob. 12ESCh. 1.8 - Rewrite the expression as a single logarithm....Ch. 1.8 - Rewrite the expression as a single logarithm....Ch. 1.8 - Rewrite the expression as a single logarithm....Ch. 1.8 - Prob. 16ESCh. 1.8 - Solve for x without using a calculating utility....Ch. 1.8 - Prob. 18ESCh. 1.8 - Solve for x without using a calculating utility....Ch. 1.8 - Prob. 20ESCh. 1.8 - Solve for x without using a calculating utility....Ch. 1.8 - Solve for x without using a calculating utility....Ch. 1.8 - Solve for x without using a calculating utility....Ch. 1.8 - Solve for x without using a calculating utility....Ch. 1.8 - Solve for x without using a calculating utility....Ch. 1.8 - Solve for x without using a calculating utility....Ch. 1.8 - Solve for x without using a calculating utility....Ch. 1.8 - Solve for x without using a calculating utility....Ch. 1.8 - Solve for x without using a calculating utility....Ch. 1.8 - Solve e2x3ex=2 for x without using a calculating...Ch. 1.8 - In each part, identify the domain and range of the...Ch. 1.8 - In each part, identify the domain and range of the...Ch. 1.8 - Determine whether the statement is true or false....Ch. 1.8 - Determine whether the statement is true or false....Ch. 1.8 - Determine whether the statement is true or false....Ch. 1.8 - Determine whether the statement is true or false....Ch. 1.8 - Prob. 39ESCh. 1.8 - Graph the functions on the same screen of a...Ch. 1.8 - Graph the functions on the same screen of a...Ch. 1.8 - (a) Derive the general change of base formula...Ch. 1.8 - Prob. 43ESCh. 1.8 - Use a graphing utility to estimate the two points...Ch. 1.8 - (a) Is the curve in the accompanying figure the...Ch. 1.8 - (a) Make a conjecture about the general shape of...Ch. 1.8 - Find the fallacy in the following “proof� that...Ch. 1.8 - Prove the four algebraic properties of logarithms...Ch. 1.8 - Prob. 49ESCh. 1.8 - Find the limits. limx+1ex1+exCh. 1.8 - Find the limits. limx+ex+exexexCh. 1.8 - Prob. 52ESCh. 1.8 - Find the limits. limx+ln2x2Ch. 1.8 - Prob. 54ESCh. 1.8 - Find the limits. limx+x+1xxxCh. 1.8 - Find the limits. limx+1+1xxCh. 1.8 - Evaluate the limit using an appropriate...Ch. 1.8 - Evaluate the limit using an appropriate...Ch. 1.8 - Prob. 59ESCh. 1.8 - Prob. 60ESCh. 1.8 - Evaluate the limit using an appropriate...Ch. 1.8 - Evaluate the limit using an appropriate...Ch. 1.8 - Evaluate the limit using an appropriate...Ch. 1.8 - Prob. 64ESCh. 1.8 - Let fx=bx, where 0b . Use the substitution...Ch. 1.8 - Prove that limx01+x1/x=e by completing parts (a)...Ch. 1.8 - Suppose that the speed (in ft/s) of a skydiver t...Ch. 1.8 - The population p of the United States (in...Ch. 1.8 - (a) Compute the (approximate) values of the terms...Ch. 1.8 - Let fx=1+1xx . (a) Prove the identity fx=xx1fx1...Ch. 1.8 - If equipment in the satellite of Example 3...Ch. 1.8 - The equation Q=12e0.055t gives the mass Q in grams...Ch. 1.8 - The acidity of a substance is measured by its pH...Ch. 1.8 - Use the definition of pH in Exercise 73 to find H+...Ch. 1.8 - The perceived loudness of a sound in decibels dB...Ch. 1.8 - Use the definition of the decibel level of a sound...Ch. 1.8 - Use the definition of the decibel level of a sound...Ch. 1.8 - Use the definition of the decibel level of a sound...Ch. 1.8 - On the Richter scale, the magnitude M of an...Ch. 1.8 - Suppose that the magnitudes of two earthquakes...Ch. 1 - In each part, complete the table and make a...Ch. 1 - (a) Approximate the value of the limit limx03x2xx...Ch. 1 - Find the limits. limx1x3x2x1Ch. 1 - Find the limits. limx1x3x2x1Ch. 1 - Prob. 7RECh. 1 - Prob. 8RECh. 1 - Find the limits. limx+2x153x2+2x7x39xCh. 1 - Find the limits. limx0x2+42x2Ch. 1 - In each part, find limxafx, if exists, where a is...Ch. 1 - Prob. 13RECh. 1 - Find the limits. limx0xsinx1cosxCh. 1 - Find the limits. limx03xsinkxx,k0Ch. 1 - Prob. 16RECh. 1 - Prob. 17RECh. 1 - Prob. 18RECh. 1 - Prob. 19RECh. 1 - Find the limits. limx+1+axbx,a,b0Ch. 1 - If $1000 is invested in an account that pays 7...Ch. 1 - (a) Write a paragraph or two that describes how...Ch. 1 - (a) Find a formula for a rational function that...Ch. 1 - The limit limx0sinxx=1 ensures that there is a...Ch. 1 - In each part, a positive number and the limit L...Ch. 1 - Use Definition 1.4.1 to prove that stated limits...Ch. 1 - (a) Let fx=sinxsin1x1 Approximate limx1fx by...Ch. 1 - Find values of x, if any, at which the given...Ch. 1 - Show that the conclusion of the Intermediate-Value...Ch. 1 - Suppose that f is continuous on the interval 0,1,...Ch. 1 - In each part, find f1x if the inverse exists. (a)...Ch. 1 - In each part, find the exact numerical value of...Ch. 1 - In each part, sketch the graph, and check your...Ch. 1 - Suppose that the graph of y=logx is drawn with...Ch. 1 - Prob. 42RECh. 1 - Express the following function as a rational...Ch. 1 - Suppose that y=Cekt, where C and k are constants,...Ch. 1 - Suppose that a package of medical supplies is...Ch. 1 - A breeding group of 20 bighorn sheep is released...Ch. 1 - An oven is preheated and then remains at a...Ch. 1 - (a) Show that for x0 and k0 the equations xk=ex...Ch. 1 - Consider fx=x2tanx+lnx,0x/2 . (a) Explain why f is...

Additional Math Textbook Solutions

Find more solutions based on key concepts
Whether the ‘Physicians Committee for Responsible Medicine’ has the potential to create a bias in a statistical...

Elementary Statistics

Normal Distributions. In Exercises 9 and 10, using a loose interpretation of the criteria for determining wheth...

Elementary Statistics (13th Edition)

In track, the second lane from the inside of the track is longer than the inside lane. Use this information to ...

A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)

NOTE: Write your answers using interval notation when appropriate. CHECKING ANALYTIC SKILLS Fill in each blank ...

Graphical Approach To College Algebra

Coke versus Pepsi (Example 5) Suppose you are testing someone to see whether she or he can tell Coke from Pepsi...

Introductory Statistics

Which of the series in Exercises 17–56 converge, and which diverge? Use any method, and give reasons for your a...

University Calculus: Early Transcendentals (4th Edition)

Knowledge Booster
Background pattern image
Calculus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Similar questions
Recommended textbooks for you
Text book image
Functions and Change: A Modeling Approach to Coll...
Algebra
ISBN:9781337111348
Author:Bruce Crauder, Benny Evans, Alan Noell
Publisher:Cengage Learning
Text book image
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Text book image
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning
Text book image
College Algebra
Algebra
ISBN:9781938168383
Author:Jay Abramson
Publisher:OpenStax
Text book image
College Algebra
Algebra
ISBN:9781337282291
Author:Ron Larson
Publisher:Cengage Learning
Text book image
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
SEE MORE TEXTBOOKS
Limits and Continuity; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=9brk313DjV8;License: Standard YouTube License, CC-BY