
Concept explainers
The nonisomorphic graphs of order 1, order 2 and order 3, and explain why the answer is
Answer to Problem 1E
The number nonisomorphic graphs of order 1 is
Explanation of Solution
Definition used:
“Two general graphs
Calculation:
By the definition of the isomorphic graphs, it is observed that the two graphs will have same number of vertices and edges having structural similarities.
Consider the case when order of a simple graph is 1. This graph will have exactly 1 vertex.
The only possible simple graph of order 1 is the graph with one vertex having no edge, which is shown below in Figure 1.
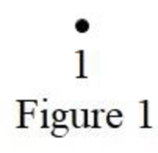
From Figure 1, it is observed that the number of nonisomorphic graphs of order 1 is
Consider the case when order of a simple graph is 2. This graph will have exactly 2 vertex.
The only possible simple graphs of order 2 is the graph with two vertex having no edge as well as one edge, which is shown below in Figure 2.
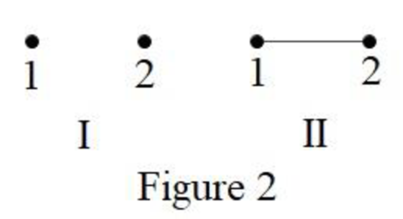
From Figure 2, it is observed that the graphs I and II are nonisomorphic.
Therefore, the number of nonisomorphic graphs of order 2 is
Consider the case when order of a simple graph is 3. This graph will have exactly 3 vertex.
There are 7 possible simple graphs of order 3, which is shown below in Figure 3.
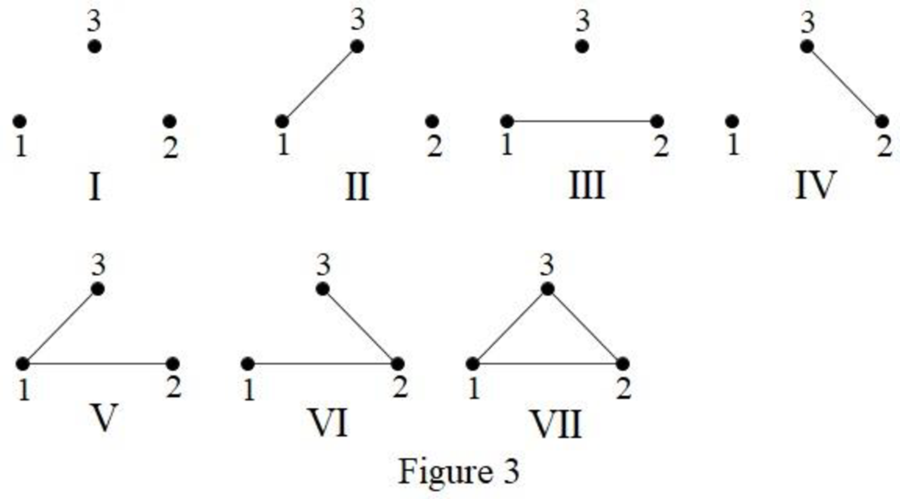
From Figure 3, it is observed that the graphs II, III and IV are isomorphic.
Also, the graphs V and VI are isomorphic.
Thus, the nonisomorphic graphs of order 3 are I, II, V and VII which has the number of edges 0, 1, 2 and 3, respectively.
Therefore, the number nonisomorphic graphs of order 3 is
In the case of general graphs, loops and multi-edges will be present.
That is, for general graphs there is no bound on the number of edges irrespective of the order. Even a single vertex may have many loops.
For example, consider the graph shown below in Figure 4.
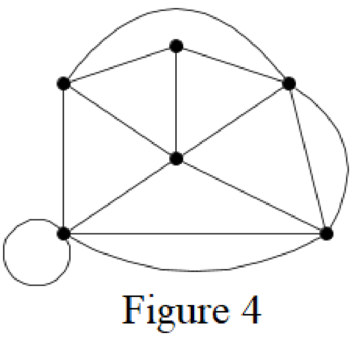
The graph in Figure 4 has multiple edges and loops. There can be many more loops and multiple edges possible in the same graph.
It is known that a graph of order n can have n loops,
Thus, for general graphs, the number of nonisomorphic graphs of order n will be infinite.
Want to see more full solutions like this?
Chapter 11 Solutions
Introductory Combinatorics
- Use the figure for Exercises 1-2. Suppose you use geometry software to construct a secant CE and tangent CD that intersect on a circle at point C. File Edit Display Construct Transform Measure Graph Window Help D 1. Suppose you measure /DCE and you measure CBE. Then you drag the points around the circle and measure the angle and arc three more times. What would you expect to find each time? Which theorem from the lesson would you be demonstrating? 2. When the measure of the intercepted arc is 180°, what is the measure of the angle? What does that tell you about the secant?arrow_forwardQ.3.2 A sample of consumers was asked to name their favourite fruit. The results regarding the popularity of the different fruits are given in the following table. Type of Fruit Number of Consumers Banana 25 Apple 20 Orange 5 TOTAL 50 Draw a bar chart to graphically illustrate the results given in the table.arrow_forwardFor the given right triangle, the longer leg is 8 units long and the shorter leg is 6 units long. sina=arrow_forward
- Q.2.3 The probability that a randomly selected employee of Company Z is female is 0.75. The probability that an employee of the same company works in the Production department, given that the employee is female, is 0.25. What is the probability that a randomly selected employee of the company will be female and will work in the Production department? Q.2.4 There are twelve (12) teams participating in a pub quiz. What is the probability of correctly predicting the top three teams at the end of the competition, in the correct order? Give your final answer as a fraction in its simplest form.arrow_forwardQ.2.1 A bag contains 13 red and 9 green marbles. You are asked to select two (2) marbles from the bag. The first marble selected will not be placed back into the bag. Q.2.1.1 Construct a probability tree to indicate the various possible outcomes and their probabilities (as fractions). Q.2.1.2 What is the probability that the two selected marbles will be the same colour? Q.2.2 The following contingency table gives the results of a sample survey of South African male and female respondents with regard to their preferred brand of sports watch: PREFERRED BRAND OF SPORTS WATCH Samsung Apple Garmin TOTAL No. of Females 30 100 40 170 No. of Males 75 125 80 280 TOTAL 105 225 120 450 Q.2.2.1 What is the probability of randomly selecting a respondent from the sample who prefers Garmin? Q.2.2.2 What is the probability of randomly selecting a respondent from the sample who is not female? Q.2.2.3 What is the probability of randomly…arrow_forwardCan you answer this question and give step by step and why and how to get it. Can you write it (numerical method)arrow_forward
- Construct tables showing the values of alI the Dirichlet characters mod k fork = 8,9, and 10. (please show me result in a table and the equation in mathematical format.)arrow_forwardExample: For what odd primes p is 11 a quadratic residue modulo p? Solution: This is really asking "when is (11 | p) =1?" First, 11 = 3 (mod 4). To use LQR, consider two cases p = 1 or 3 (mod 4): p=1 We have 1 = (11 | p) = (p | 11), so p is a quadratic residue modulo 11. By brute force: 121, 224, 3² = 9, 4² = 5, 5² = 3 (mod 11) so the quadratic residues mod 11 are 1,3,4,5,9. Using CRT for p = 1 (mod 4) & p = 1,3,4,5,9 (mod 11). p = 1 (mod 4) & p = 1 (mod 11 gives p 1 (mod 44). p = 1 (mod 4) & p = 3 (mod 11) gives p25 (mod 44). p = 1 (mod 4) & p = 4 (mod 11) gives p=37 (mod 44). p = 1 (mod 4) & p = 5 (mod 11) gives p 5 (mod 44). p = 1 (mod 4) & p=9 (mod 11) gives p 9 (mod 44). So p =1,5,9,25,37 (mod 44).arrow_forwardCan you answer this question and give step by step and why and how to get it. Can you write it (numerical method)arrow_forward
- Jamal wants to save $48,000 for a down payment on a home. How much will he need to invest in an account with 11.8% APR, compounding daily, in order to reach his goal in 10 years? Round to the nearest dollar.arrow_forwardr nt Use the compound interest formula, A (t) = P(1 + 1)". An account is opened with an intial deposit of $7,500 and earns 3.8% interest compounded semi- annually. Round all answers to the nearest dollar. a. What will the account be worth in 10 years? $ b. What if the interest were compounding monthly? $ c. What if the interest were compounded daily (assume 365 days in a year)? $arrow_forwardKyoko has $10,000 that she wants to invest. Her bank has several accounts to choose from. Her goal is to have $15,000 by the time she finishes graduate school in 7 years. To the nearest hundredth of a percent, what should her minimum annual interest rate be in order to reach her goal assuming they compound daily? (Hint: solve the compound interest formula for the intrerest rate. Also, assume there are 365 days in a year) %arrow_forward
 Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education
Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
 Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON
Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning,
Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning, Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education
Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education





