
To use a software to create Normal quantile plots for each of the three groups of the forest plots and explain are the three distributions roughly Normal and what are the most prominent deviations from Normality that you see.
Answer to Problem 11.51E
Yes, the three groups are roughly Normal.
Explanation of Solution
In the question, the data is given that described of the effects of logging on counts in the Borneo rainforest as:
Thus, we will use the excel to construct the Normal quantile plot by using z-scores. And the excel
So, for group one, we have the following calculation as:
| Group 1 | Rank | Rank proportion | Rank based z score | Group 1 |
| 16 | 1 | =(AA81-0.5)/COUNT($Z$81:$Z$92) | =NORMSINV(AB81) | 16 |
| 19 | 2 | =(AA82-0.5)/COUNT($Z$81:$Z$92) | =NORMSINV(AB82) | 19 |
| 19 | 3 | =(AA83-0.5)/COUNT($Z$81:$Z$92) | =NORMSINV(AB83) | 19 |
| 20 | 4 | =(AA84-0.5)/COUNT($Z$81:$Z$92) | =NORMSINV(AB84) | 20 |
| 21 | 5 | =(AA85-0.5)/COUNT($Z$81:$Z$92) | =NORMSINV(AB85) | 21 |
| 22 | 6 | =(AA86-0.5)/COUNT($Z$81:$Z$92) | =NORMSINV(AB86) | 22 |
| 24 | 7 | =(AA87-0.5)/COUNT($Z$81:$Z$92) | =NORMSINV(AB87) | 24 |
| 27 | 8 | =(AA88-0.5)/COUNT($Z$81:$Z$92) | =NORMSINV(AB88) | 27 |
| 27 | 9 | =(AA89-0.5)/COUNT($Z$81:$Z$92) | =NORMSINV(AB89) | 27 |
| 28 | 10 | =(AA90-0.5)/COUNT($Z$81:$Z$92) | =NORMSINV(AB90) | 28 |
| 29 | 11 | =(AA91-0.5)/COUNT($Z$81:$Z$92) | =NORMSINV(AB91) | 29 |
| 33 | 12 | =(AA92-0.5)/COUNT($Z$81:$Z$92) | =NORMSINV(AB92) | 33 |
The result is as:
| Group 1 | Rank | Rank proportion | Rank based z score | Group 1 |
| 16 | 1 | 0.041667 | -1.73166 | 16 |
| 19 | 2 | 0.125 | -1.15035 | 19 |
| 19 | 3 | 0.208333 | -0.81222 | 19 |
| 20 | 4 | 0.291667 | -0.54852 | 20 |
| 21 | 5 | 0.375 | -0.31864 | 21 |
| 22 | 6 | 0.458333 | -0.10463 | 22 |
| 24 | 7 | 0.541667 | 0.104633 | 24 |
| 27 | 8 | 0.625 | 0.318639 | 27 |
| 27 | 9 | 0.708333 | 0.548522 | 27 |
| 28 | 10 | 0.791667 | 0.812218 | 28 |
| 29 | 11 | 0.875 | 1.150349 | 29 |
| 33 | 12 | 0.958333 | 1.731664 | 33 |
Thus, we will select the last two column and then go to the insert tab and select the chart option and then select the plot, so the normal quantile plot is as:
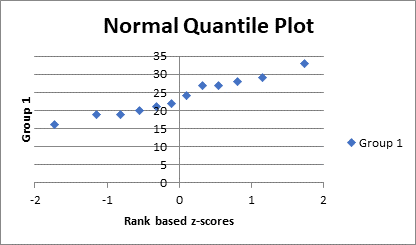
So, for the group two we have the calculation as:
| Group 2 | Rank | Rank proportion | Rank based z score | Group 2 |
| 2 | 1 | =(AG81-0.5)/COUNT($AF$81:$AF$92) | =NORMSINV(AH81) | 2 |
| 9 | 2 | =(AG82-0.5)/COUNT($AF$81:$AF$92) | =NORMSINV(AH82) | 9 |
| 12 | 3 | =(AG83-0.5)/COUNT($AF$81:$AF$92) | =NORMSINV(AH83) | 12 |
| 12 | 4 | =(AG84-0.5)/COUNT($AF$81:$AF$92) | =NORMSINV(AH84) | 12 |
| 14 | 5 | =(AG85-0.5)/COUNT($AF$81:$AF$92) | =NORMSINV(AH85) | 14 |
| 14 | 6 | =(AG86-0.5)/COUNT($AF$81:$AF$92) | =NORMSINV(AH86) | 14 |
| 15 | 7 | =(AG87-0.5)/COUNT($AF$81:$AF$92) | =NORMSINV(AH87) | 15 |
| 17 | 8 | =(AG88-0.5)/COUNT($AF$81:$AF$92) | =NORMSINV(AH88) | 17 |
| 17 | 9 | =(AG89-0.5)/COUNT($AF$81:$AF$92) | =NORMSINV(AH89) | 17 |
| 18 | 10 | =(AG90-0.5)/COUNT($AF$81:$AF$92) | =NORMSINV(AH90) | 18 |
| 19 | 11 | =(AG91-0.5)/COUNT($AF$81:$AF$92) | =NORMSINV(AH91) | 19 |
| 20 | 12 | =(AG92-0.5)/COUNT($AF$81:$AF$92) | =NORMSINV(AH92) | 20 |
Thus, the result is as:
| Group 2 | Rank | Rank proportion | Rank based z score | Group 2 |
| 2 | 1 | 0.0416667 | -1.731664396 | 2 |
| 9 | 2 | 0.125 | -1.15034938 | 9 |
| 12 | 3 | 0.2083333 | -0.812217801 | 12 |
| 12 | 4 | 0.2916667 | -0.548522283 | 12 |
| 14 | 5 | 0.375 | -0.318639364 | 14 |
| 14 | 6 | 0.4583333 | -0.104633456 | 14 |
| 15 | 7 | 0.5416667 | 0.104633456 | 15 |
| 17 | 8 | 0.625 | 0.318639364 | 17 |
| 17 | 9 | 0.7083333 | 0.548522283 | 17 |
| 18 | 10 | 0.7916667 | 0.812217801 | 18 |
| 19 | 11 | 0.875 | 1.15034938 | 19 |
| 20 | 12 | 0.9583333 | 1.731664396 | 20 |
Thus, we will select the last two column and then go to the insert tab and select the chart option and then select the plot, so the normal quantile plot is as:
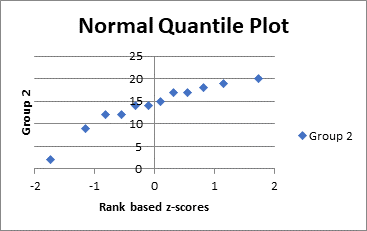
So, for the group three we have the calculation as:
| Group3 | Rank | Rank proportion | Rank based z score | Group3 |
| 4 | 1 | =(T81-0.5)/COUNT($S$81:$S$89) | =NORMSINV(U81) | 4 |
| 12 | 2 | =(T82-0.5)/COUNT($S$81:$S$89) | =NORMSINV(U82) | 12 |
| 12 | 3 | =(T83-0.5)/COUNT($S$81:$S$89) | =NORMSINV(U83) | 12 |
| 15 | 4 | =(T84-0.5)/COUNT($S$81:$S$89) | =NORMSINV(U84) | 15 |
| 18 | 5 | =(T85-0.5)/COUNT($S$81:$S$89) | =NORMSINV(U85) | 18 |
| 18 | 6 | =(T86-0.5)/COUNT($S$81:$S$89) | =NORMSINV(U86) | 18 |
| 19 | 7 | =(T87-0.5)/COUNT($S$81:$S$89) | =NORMSINV(U87) | 19 |
| 22 | 8 | =(T88-0.5)/COUNT($S$81:$S$89) | =NORMSINV(U88) | 22 |
| 22 | 9 | =(T89-0.5)/COUNT($S$81:$S$89) | =NORMSINV(U89) | 22 |
The result is as:
| Group3 | Rank | Rank proportion | Rank based z score | Group3 |
| 4 | 1 | 0.055555556 | -1.593218818 | 4 |
| 12 | 2 | 0.166666667 | -0.967421566 | 12 |
| 12 | 3 | 0.277777778 | -0.589455798 | 12 |
| 15 | 4 | 0.388888889 | -0.282216147 | 15 |
| 18 | 5 | 0.5 | 0 | 18 |
| 18 | 6 | 0.611111111 | 0.282216147 | 18 |
| 19 | 7 | 0.722222222 | 0.589455798 | 19 |
| 22 | 8 | 0.833333333 | 0.967421566 | 22 |
| 22 | 9 | 0.944444444 | 1.593218818 | 22 |
Thus, we will select the last two column and then go to the insert tab and select the chart option and then select the plot, so the normal quantile plot is as:
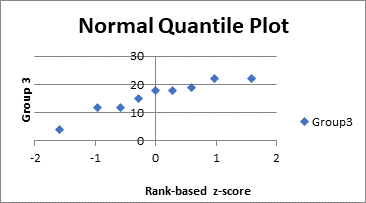
Thus, we can see that in the three groups the points are approximately in a straight line and increasing in nature. Thus, we can say that the three groups are approximately follows
Want to see more full solutions like this?
Chapter 11 Solutions
Practice of Statistics in the Life Sciences
- Obtain the linear equation for trend for time series with St² = 140, Ey = 16.91 and Σty= 62.02, m n = 7arrow_forwardA quality characteristic of a product is normally distributed with mean μ and standard deviation σ = 1. Speci- fications on the characteristic are 6≤x≤8. A unit that falls within specifications on this quality characteristic results in a profit of Co. However, if x 8, the profit is -C2. Find the value ofμ that maximizes the expected profit.arrow_forwardA) The output voltage of a power supply is normally distributed with mean 5 V and standard deviation 0.02 V. If the lower and upper specifications for voltage are 4.95 V and 5.05 V, respectively, what is the probability that a power supply selected at random conform to the specifications on voltage? B) Continuation of A. Reconsider the power supply manufacturing process in A. Suppose We wanted to improve the process. Can shifting the mean reduce the number of nonconforming units produced? How much would the process variability need to be reduced in order to have all but one out of 1000 units conform to the specifications?arrow_forward
- der to complete the Case X T Civil Service Numerical Test Sec X T Casework Skills Practice Test Maseline Vaseline x + euauthoring.panpowered.com/DeliveryWeb/Civil Service Main/84589a48-6934-4b6e-a6e1-a5d75f559df9?transferToken-News NGSSON The table below shows the best price available for various items from 4 uniform suppliers. The prices do not include VAT (charged at 20%). Item Waterproof boots A1-Uniforms (£)Best Trade (£)Clothing Tech (£)Dress Right (£) 59.99 39.99 59.99 49.99 Trousers 9.89 9.98 9.99 11.99 Shirts 14.99 15.99 16.99 12.99 Hi-Vis vest 4.49 4.50 4.00 4.00 20.00 25.00 19.50 19.99 Hard hats A company needs to buy a set of 12 uniforms which includes 1 of each item. If the special offers are included which supplier is cheapest? OOO A1-Uniforms Best Trade Clothing Tech Q Search + ** 109 8 CO* F10 Home F11 F12 6arrow_forwardto complete the Case × T Civil Service Numerical Test Sec x T Casework Skills Practice Test + Vaseline euauthoring.panpowered.com/DeliveryWeb/Civil Service Main/84589a48-b934-4b6e-a6e1-a5d75f559df9?transferToken=MxNewOS NGFSPSZSMOMzuz The table below shows the best price available for various items from 4 uniform suppliers. The prices do not include VAT (charged at 20%). Item A1-Uniforms (£)Best Trade (£)Clothing Tech (£)Dress Right (£) Waterproof boots 59.99 39.99 59.99 49.99 Trousers 9.89 9.98 9.99 11.99 Shirts 14.99 15.99 16.99 12.99 Hi-Vis vest 4.49 4.50 4.00 4.00 20.00 25.00 19.50 19.99 Hard hats A company needs to buy a set of 12 uniforms which includes 1 of each item. If the special offers are included, which supplier is cheapest? O O O O A1-Uniforms Best Trade Clothing Tech Dress Right Q Search ENG L UK +0 F6 四吧 6 78 ㄓ F10 9% * CO 1 F12 34 Oarrow_forwardCritics review films out of 5 based on three attributes: the story, the special effects and the acting. The ratings of four critics for a film are collected in the table below.CriticSpecialStory rating Effects rating Acting rating Critic 14.44.34.5Critic 24.14.23.9Critic 33.943.4Critic 44.24.14.2Critic 1 also gave the film a rating for the Director's ability. If the average of Critic 1's ratings was 4.3 what rating did they give to the Director's ability?3.94.04.14.24.3arrow_forward
- Two measurements are made of some quantity. For the first measurement, the average is 74.4528, the RMS error is 6.7441, and the uncertainty of the mean is 0.9264. For the second one, the average is 76.8415, the standard deviation is 8.3348, and the uncertainty of the mean is 1.1448. The expected value is exactly 75. 13. Express the first measurement in public notation. 14. Is there a significant difference between the two measurements? 1 15. How does the first measurement compare with the expected value? 16. How does the second measurement compare with the expected value?arrow_forwardA hat contains slips of paper numbered 1 through 6. You draw two slips of paper at random from the hat,without replacing the first slip into the hat.(a) (5 points) Write out the sample space S for this experiment.(b) (5 points) Express the event E : {the sum of the numbers on the slips of paper is 4} as a subset of S.(c) (5 points) Find P(E)(d) (5 points) Let F = {the larger minus the smaller number is 0}. What is P(F )?(e) (5 points) Are E and F disjoint? Why or why not?(f) (5 points) Find P(E ∪ F )arrow_forwardIn addition to the in-school milk supplement program, the nurse would like to increase the use of daily vitamin supplements for the children by visiting homes and educating about the merits of vitamins. She believes that currently, about 50% of families with school-age children give the children a daily megavitamin. She would like to increase this to 70%. She plans a two-group study, where one group serves as a control and the other group receives her visits. How many families should she expect to visit to have 80% power of detecting this difference? Assume that drop-out rate is 5%.arrow_forward
- A recent survey of 400 americans asked whether or not parents do too much for their young adult children. The results of the survey are shown in the data file. a) Construct the frequency and relative frequency distributions. How many respondents felt that parents do too much for their adult children? What proportion of respondents felt that parents do too little for their adult children? b) Construct a pie chart. Summarize the findingsarrow_forwardThe average number of minutes Americans commute to work is 27.7 minutes (Sterling's Best Places, April 13, 2012). The average commute time in minutes for 48 cities are as follows: Click on the datafile logo to reference the data. DATA file Albuquerque 23.3 Jacksonville 26.2 Phoenix 28.3 Atlanta 28.3 Kansas City 23.4 Pittsburgh 25.0 Austin 24.6 Las Vegas 28.4 Portland 26.4 Baltimore 32.1 Little Rock 20.1 Providence 23.6 Boston 31.7 Los Angeles 32.2 Richmond 23.4 Charlotte 25.8 Louisville 21.4 Sacramento 25.8 Chicago 38.1 Memphis 23.8 Salt Lake City 20.2 Cincinnati 24.9 Miami 30.7 San Antonio 26.1 Cleveland 26.8 Milwaukee 24.8 San Diego 24.8 Columbus 23.4 Minneapolis 23.6 San Francisco 32.6 Dallas 28.5 Nashville 25.3 San Jose 28.5 Denver 28.1 New Orleans 31.7 Seattle 27.3 Detroit 29.3 New York 43.8 St. Louis 26.8 El Paso 24.4 Oklahoma City 22.0 Tucson 24.0 Fresno 23.0 Orlando 27.1 Tulsa 20.1 Indianapolis 24.8 Philadelphia 34.2 Washington, D.C. 32.8 a. What is the mean commute time for…arrow_forwardMorningstar tracks the total return for a large number of mutual funds. The following table shows the total return and the number of funds for four categories of mutual funds. Click on the datafile logo to reference the data. DATA file Type of Fund Domestic Equity Number of Funds Total Return (%) 9191 4.65 International Equity 2621 18.15 Hybrid 1419 2900 11.36 6.75 Specialty Stock a. Using the number of funds as weights, compute the weighted average total return for these mutual funds. (to 2 decimals) % b. Is there any difficulty associated with using the "number of funds" as the weights in computing the weighted average total return in part (a)? Discuss. What else might be used for weights? The input in the box below will not be graded, but may be reviewed and considered by your instructor. c. Suppose you invested $10,000 in this group of mutual funds and diversified the investment by placing $2000 in Domestic Equity funds, $4000 in International Equity funds, $3000 in Specialty Stock…arrow_forward
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman





