
Determine the moments at A,B, and C, then draw the moment diagram for the beam. The moment of inertia of each span is indicated in the figure. Assume the support at B is a roller and A and C are fixed. E = 29(103) ksi.
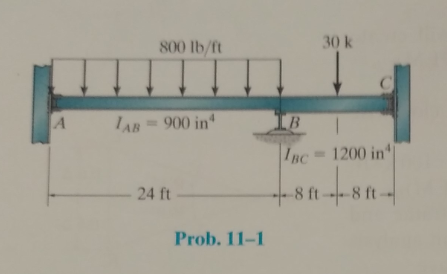
The moments at A, B, and C, and to draw the moment diagram for the beam.
Answer to Problem 11.1P
The moment at A for member AB is,
The moment at B for member BA is,
The moment at B for member BC is,
The moment at C for member CB is,
The following figure shows the moment diagram of the beam.
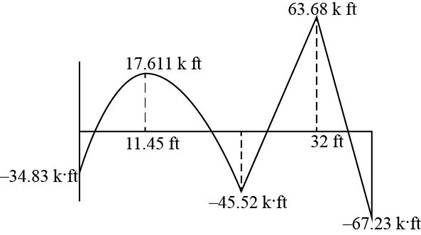
Explanation of Solution
Calculation:
The following figure shows the beam diagram.
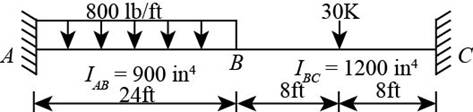
Figure-(1)
Calculate the fixed end moments at every end as shown below.
Calculate fixed end moments of member AB.
Here, given load is
Substitute
Calculate fixed end moments of member BA.
Substitute
Calculate fixed end moments of member BC.
Substitute
Calculate fixed end moments of member CB.
Substitute
Calculate the member relative stiffness factors on either side of B.
Calculate relative stiffness of member BA.
Here,
Substitute
Calculate relative stiffness of member BC.
Substitute
Calculate the distribution factors for different members.
Calculate distribution factors for AB.
Calculate distribution factors for BA.
Substitute
Substitute
Calculate distribution factors for BC.
Substitute
Substitute
Calculate distribution factors for CB.
Calculate the balance moment for each member as shown below.
Calculate balance moment foe BA.
Calculate balance moment for BC.
Draw the moment distribution table as shown below.
| Joints | A | B | C | |
| Member | AB | BA | BC | CB |
| DF | | | | |
| FEM | | | | |
| Balance | - | | | - |
| Carry over moment | | | | |
| Balance | | | | |
| | | | | |
Consider the section AB as shown below.
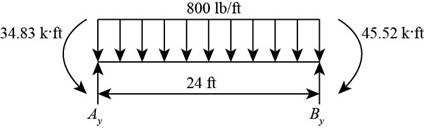
Figure-(2)
Write the Equation for sum of vertical forces.
Here, vertical reaction at A and B are
Write the Equation for sum of moment about A.
Substitute
Calculate the distance at which shear force changing its sign for maximum moment.
Write the Equation for shear force at distance
Equate the value of shear force to zero for distance.
Calculate the value of maximum moment at a distance of
Consider the section BC as shown below.
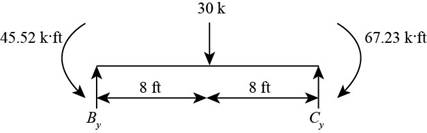
Figure-(3)
Write the Equation for sum of vertical forces.
Write the Equation for sum of moment about B.
Here, vertical reaction at C is
Substitute
For member BC, moment will be maximum at the center.
Calculate maximum moment at the center of BC.
Conclusion:
The moment at A for member AB is,
The moment at B for member BA is,
The moment at B for member BC is,
The moment at C for member CB is,
The following diagram shows the moment diagram of the beam.
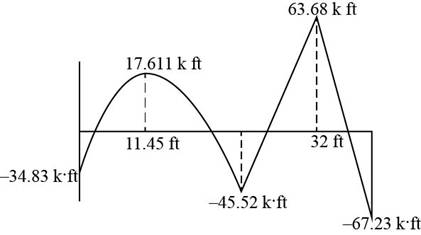
Figure-(4)
Want to see more full solutions like this?
Chapter 11 Solutions
Structural Analysis, Student Value Edition
Additional Engineering Textbook Solutions
Elementary Surveying: An Introduction To Geomatics (15th Edition)
Database Concepts (8th Edition)
Java: An Introduction to Problem Solving and Programming (8th Edition)
Web Development and Design Foundations with HTML5 (8th Edition)
Java How to Program, Early Objects (11th Edition) (Deitel: How to Program)
Starting Out with Programming Logic and Design (5th Edition) (What's New in Computer Science)
- A sample of Achilles saturated with water has a mass of 1710 g. After heating in an oven, a constant mass of 1815 g is obtained. The density of solid Achilles seeds is 2.78 g/cm3. We are asked to calculate: a) The water content and void ratio b) The porosity and specific gravity of the clayey soil c) The wet density of the clayey soil, the corresponding dry density and dry densityarrow_forward8. A prestressed concrete beam is subjected to the following stress distributions: Pi is the initial prestressing force, Pe is the effective prestressing force, M, is the bending moment due to self- weight, Ma and M, are the dead load and live load bending moment, respectively. The concrete has the following properties: fr = 6000 psi and fri = 4200 psi +250 -85 -2500 +550 Pe+ Mo+Ma+Mi P alone P₁+ Mo -2450 -3500 Stress at midspan +210 +250 P, alone Pe alone -2500 -3500 Stress at ends Using Table 22.1, evaluate whether the stresses at the center of the span and the end of the span comply with the permissible stress limits. The beam is classified as U-class. Provide justifications for each condition listed in the table. Note: Calculated stresses are to be taken from the above diagram, and permissible stresses are to be calculated using Table 22.1. Compressive stresses immediately after transfer Tensile stresses immediately after transfer Compressive stresses under sustained and total…arrow_forward10. A short column is subjected to an eccentric loading. The axial load P = 1000 kips and the eccentricity e = 12 in. The material strengths are fy = 60 ksi and f = 6000 psi. The Young's modulus of steel is 29000 ksi. (a) Fill in the blanks in the interaction diagram shown below. (2pts each, 10pt total) Po Pn (1) failure range H 3" 30" Ast 6 No. 10 bars = P 22" I e H 3" (4) e = e small Load path for given e Radial lines show constant (2) eb (3) e large failure range Mn (5) e= Mo (b) Compute the balanced failure point, i.e., P and Mb.arrow_forward
- No chatgpt plsarrow_forward11. The prestressed T beam shown below is pretensioned using low relaxation stress-relieved Grade 270 strands. The steel area Aps = 2.5 in². The tensile strength is fpu = 270 ksi, and the concrete compressive strength is fr = 6000 psi. (a) Calculate the nominal moment strength Mn with hr = 6 in. 22" 15" T hf (b) Since this beam is a T-beam, the nominal moment strength M₁ increases with a thicker hf. However, M, stops increasing if he reaches a value. Determine the minimum thickness hy that can achieve the maximum nominal moment strength Mr. Also, calculate the corresponding maximum nominal moment strength Mn with the computed hf.arrow_forward10. A short column is subjected to an eccentric loading. The axial load P = 1000 kips and the eccentricity e = 12 in. The material strengths are fy = 60 ksi and f = 6000 psi. The Young's modulus of steel is 29000 ksi. (a) Fill in the blanks in the interaction diagram shown below. 30" Ast 6 No. 10 bars = Pn (1) Po (4) e = e small Load path for given e failure range Radial lines show constant (2) eb (3) e large failure range Mn (5) e= Mo (b) Compute the balanced failure point, i.e., P and Mb. H 3" P 22" I e H 3"arrow_forward
- 10. A short column is subjected to an eccentric loading. The axial load P = 1000 kips and the eccentricity e = 12 in. The material strengths are fy = 60 ksi and f = 6000 psi. The Young's modulus of steel is 29000 ksi. (a) Fill in the blanks in the interaction diagram shown below. 30" Ast 6 No. 10 bars = Pn (1) Po (4) e = e small Load path for given e failure range Radial lines show constant (2) eb (3) e large failure range Mn (5) e= Mo (b) Compute the balanced failure point, i.e., P and Mb. H 3" P 22" I e H 3"arrow_forward7. Match the given strand profiles with the corresponding loading conditions for a prestressed concrete (PSC) beam. Strand profile (b) (d) (c) (a) Ꮎ Load on a beamarrow_forward4. For serviceability considerations, the effective moment of inertia (Ie) is calculated using the following formula: le 1 - 1cr ((2/3) Mcr) Ma 2 - وا ≥ Note that the upper bound was previously set as Iut in the earlier ACI equation. (a) Arrange the following moment of inertia values in ascending order (from smallest to largest): le, Ier, Ig and lut (b) Mer is the cracking moment. Choose the cross-section that should be used to compute Mcr. NA. h 5. Identify and circle the figure that represents the scenario in which the torsional effect is permitted to be reduced according to the ACI code provisions. (3 pts) mt mi B (b)arrow_forward
- I will rate, thanksarrow_forward. 9. A reinforced concrete beam is subjected to V/ = 40 kips and Tu/ = 12 ft kips at the critical section. Given conditions: ⚫ Longitudinal reinforcements use No. 8 grade 60 steel with an effective depth d = 20 in. For shear capacity, V = 18 kips and V₂ = 22 kips • For transverse reinforcements, use No. 3 bars with grade 60. • The effective torsional area of A. = 150 in². • Crack angle = 45° ⚫ The minimum stirrup spacing is Smin = 4" and the maximum stirrup spacing is Smax = Find the required stirrup spacing at the critical section. 8".arrow_forward3. The beam shown on the right uses three No. 8 bars made of Grade 60 steel as longitudinal reinforcement. The allowable maximum center-to-center spacing of the longitudinal rebars has been determined to be 10 inches. Now assume that Grade 80 steel will be used instead. Determine whether the beam satisfies the rebar spacing requirements according to the ACI Code. Additional assumptions: • Estimate fs = fy • 20" Clear cover: ? 12" Clear side cover: 1.5" The clear cover depth cc and the clear side cover remain unchanged, regardless of the change in material.arrow_forward

 Steel Design (Activate Learning with these NEW ti...Civil EngineeringISBN:9781337094740Author:Segui, William T.Publisher:Cengage Learning
Steel Design (Activate Learning with these NEW ti...Civil EngineeringISBN:9781337094740Author:Segui, William T.Publisher:Cengage Learning Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781305081550Author:Braja M. DasPublisher:Cengage Learning
Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781305081550Author:Braja M. DasPublisher:Cengage Learning Residential Construction Academy: House Wiring (M...Civil EngineeringISBN:9781285852225Author:Gregory W FletcherPublisher:Cengage Learning
Residential Construction Academy: House Wiring (M...Civil EngineeringISBN:9781285852225Author:Gregory W FletcherPublisher:Cengage Learning Materials Science And Engineering PropertiesCivil EngineeringISBN:9781111988609Author:Charles GilmorePublisher:Cengage Learning
Materials Science And Engineering PropertiesCivil EngineeringISBN:9781111988609Author:Charles GilmorePublisher:Cengage Learning Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning
Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning





