
Concept explainers
A quantitative measure of how efficiently spheres pack into unit cells is called packing efficiency, which is the percentage of the cell space occupied by the spheres. Calculate the packing efficiencies of a simple cubic cell, a body-centered cubic cell, and a face-centered cubic cell. (Hint: Refer to Figure 11.22 and use the relationship that the volume of a sphere is
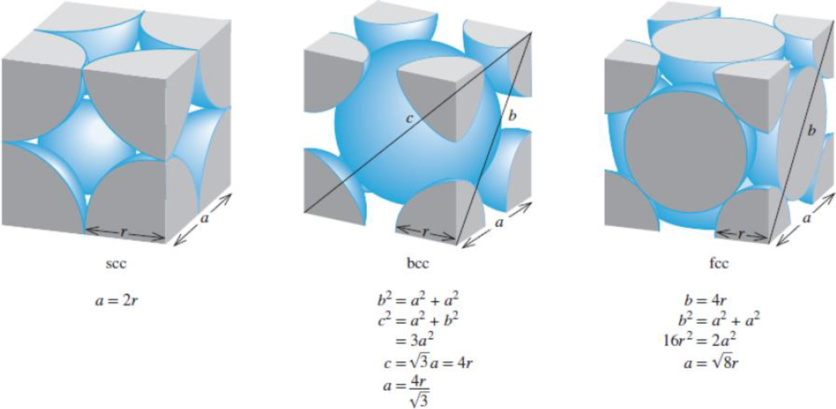
Figure 11.22 The relationship between the edge length (a) and radius (r) of atoms in the simple cubic cell, body-centered cubic cell, and face-centered cubic cell.
Interpretation: Packing efficiency of a simple cubic cell, body-centred cubic and face-centred cubic unit cells, have to be calculated.
Concept Introduction:
The major types of cubic unit cells are:
- Simple cubic unit cell.
- Face-centered cubic unit cell.
- Body-centered cubic unit cell.
Packing efficiency, is the percentage of the cell space occupied by the spheres in a cubic unit cell of any type. The atoms in the unit cells are considered as spheres.
Answer to Problem 11.134QP
The packing efficiency of a simple cubic unit cell is
The packing efficiency of a body-centred cubic unit cell is
The packing efficiency of a face-centered cubic unit cell is
Explanation of Solution
Calculating the packing efficiency for a simple cubic unit cell:
Edge length is
The relation between edge length and volume is
So the volume of the unit cell is
The number of atoms in the simple cubic unit cell is 1.
An atom is considered as sphere.
The volume of sphere is
So, the volume of atoms in the simple cubic unit cell can be expressed as:
Thus, the packing efficiency of a simple cubic unit cell is
Calculating the packing efficiency for a body-centered cubic unit cell:
Edge length is
The relation between edge length and volume is
So the volume of the unit cell is
The number of atoms in the body-centered cubic unit cell is 2.
An atom is considered as sphere.
The volume of sphere is
So, the volume of atoms in the body-centered cubic unit cell can be expressed as:
Thus, the packing efficiency of a body-centered cubic unit cell is
Calculating the packing efficiency for a face-centered cubic unit cell:
Edge length is
The relation between edge length and volume is
So the volume of the unit cell is
The number of atoms in the body-centered cubic unit cell is 4.
An atom is considered as sphere.
The volume of sphere is
So, the volume of atoms in the body-centered cubic unit cell can be expressed as:
Thus, the packing efficiency of a face-centered cubic unit cell is
Using figure 11.2 as reference, the packing efficiency for the different types of cubic unit cells have been calculated.
Want to see more full solutions like this?
Chapter 11 Solutions
CHEMISTRY-ALEKS 360 ACCESS
- 10. Stereochemistry. Assign R/S stereochemistry for the chiral center indicated on the following compound. In order to recieve full credit, you MUST SHOW YOUR WORK! H₂N CI OH CI カー 11. () Stereochemistry. Draw all possible stereoisomers of the following compound. Assign R/S configurations for all stereoisomers and indicate the relationship between each as enantiomer, diastereomer, or meso. NH2 H HNH, -18arrow_forwardb) 8. Indicate whether the following carbocation rearrangements are likely to occur Please explain your rational using 10 words or less not likely to occur • The double bond is still in the Same position + Likely to oc occur WHY? -3 H3C Brave Chair Conformers. Draw the chair conformer of the following substituted cyclohexane. Peform a RING FLIP and indicate the most stable conformation and briefly explain why using 20 words or less. CI 2 -cobs ?? MUST INDICATE H -2 -2 Br EQ Cl OR AT Br H& most stable WHY? - 4arrow_forwardCH 12 Conformational Analysis. Draw all 6 conformers (one above each letter) of the compound below looking down the indicated bond. Write the letter of the conformer with the HIGHEST and LOWEST in energies on the lines provided. NOTE: Conformer A MUST be the specific conformer of the structure as drawn below -4 NOT HOH OH 3 Conformer A: Br OH A Samo Br H 04 Br H H3 CH₂ H anti stagere Br CH clipsed H Brott H IV H MISSING 2 -2 B C D E F X 6 Conformer with HIGHEST ENERGY: 13. (1 structure LOWEST ENERGY: Nomenclature. a) Give the systematic (IUPAC) name structure. b) Draw the corresponding to this name. HINT: Do not forget to indicate stereochemistry when applicable. a) ८८ 2 "Br {t༐B,gt)-bemn€-nehpརི་ཚ༐lnoa Parent name (noname) 4 Bromo Sub = 2-methylethyl-4 Bromo nonane b) (3R,4S)-3-chloro-4-ethyl-2,7-dimethyloctane # -2 -2arrow_forward
- in the scope of the SCH4U course! please show all steps as im still learning how to format my answers in the format given, thank you!arrow_forwardhelp me solve this HWarrow_forwardMolecules of the form AH2 can exist in two potential geometries: linear or bent. Construct molecular orbital diagrams for linear and bent CH2. Identify the relevant point group, include all of the appropriate symmetry labels and pictures, and fill in the electrons. Which geometry would you predict to be more stable, and why? (Please draw out the diagram and explain)arrow_forward
 General Chemistry - Standalone book (MindTap Cour...ChemistryISBN:9781305580343Author:Steven D. Gammon, Ebbing, Darrell Ebbing, Steven D., Darrell; Gammon, Darrell Ebbing; Steven D. Gammon, Darrell D.; Gammon, Ebbing; Steven D. Gammon; DarrellPublisher:Cengage Learning
General Chemistry - Standalone book (MindTap Cour...ChemistryISBN:9781305580343Author:Steven D. Gammon, Ebbing, Darrell Ebbing, Steven D., Darrell; Gammon, Darrell Ebbing; Steven D. Gammon, Darrell D.; Gammon, Ebbing; Steven D. Gammon; DarrellPublisher:Cengage Learning ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning
ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning Chemistry: An Atoms First ApproachChemistryISBN:9781305079243Author:Steven S. Zumdahl, Susan A. ZumdahlPublisher:Cengage Learning
Chemistry: An Atoms First ApproachChemistryISBN:9781305079243Author:Steven S. Zumdahl, Susan A. ZumdahlPublisher:Cengage Learning
 Chemistry & Chemical ReactivityChemistryISBN:9781337399074Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning
Chemistry & Chemical ReactivityChemistryISBN:9781337399074Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning Chemistry: Principles and PracticeChemistryISBN:9780534420123Author:Daniel L. Reger, Scott R. Goode, David W. Ball, Edward MercerPublisher:Cengage Learning
Chemistry: Principles and PracticeChemistryISBN:9780534420123Author:Daniel L. Reger, Scott R. Goode, David W. Ball, Edward MercerPublisher:Cengage Learning





