
Concept explainers
Determine the ohms-per-mil-foot of an aluminum conductor located in an area with a temperature of 104°F (40°C).
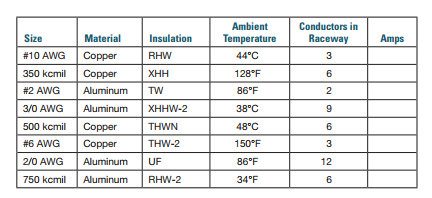
Use the NEC to determine the ampacity of the following conductors.
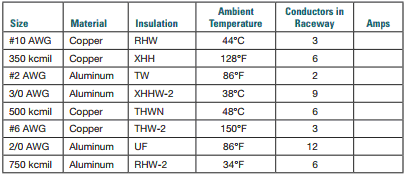
To find:
The ohms-per-mil-foot of an aluminum conductor located in an area with a temperature of 104°F (40°C). Also, use the NEC to determine the ampacity of the following conductors.
Answer to Problem 10PP
The resistance of a 16 AWG copper conductor is 1.27 ohms.
Explanation of Solution
The resistivity, K of the conductor at temperature T is
where, Rref is the resistance at 20°C
From Figure 10-16, the value of Rref can be obtained
Tref is the reference temperature (20°C)
Substituting the values, we get
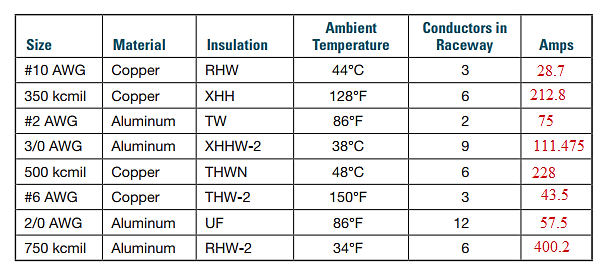
(a) From Table 310.15(B)(16), we know that the maximum ampacity of a 10 AWG copper conductor of Type RHW insulation is 35A and the rated temperature is
Thus, from Table 310.15(B)(2)(a), the correction factor of the ambient air temperature at
Thus, after correction, the ampacity will be
(b) From Table 310.15(B)(16), we know that the maximum ampacity of a 350 kcmil copper conductor of Type XHH insulation is 350A and the rated temperature is
Thus, from Table 310.15(B)(2)(a), the correction factor of the ambient air temperature at
Thus, after correction, the ampacity will be
If a raceway is to contain more than three conductors, the ampacity of the conductors must be de-rated. The correction factors for six copper conductors is 80%. Thus, after correction, the ampacity will be
(c) From Table 310.15(B)(16), we know that the maximum ampacity of a 2 AWG aluminum conductor of Type TW insulation is 75A and the rated temperature is
Thus, from Table 310.15(B)(2)(a), the correction factor of the ambient air temperature at
Thus, after correction, the ampacity will be
(d) From Table 310.15(B)(16), we know that the maximum ampacity of a 3/0 AWG aluminum conductor of Type XHHW-2 insulation is 175A and the rated temperature is
Thus, from Table 310.15(B)(2)(a), the correction factor of the ambient air temperature at
Thus, after correction, the ampacity will be
If a raceway is to contain more than three conductors, the ampacity of the conductors must be de-rated. The correction factors for nine aluminum conductors is 70%. Thus, after correction, the ampacity will be
(e) From Table 310.15(B)(16), we know that the maximum ampacity of a 500 kcmil copper conductor of Type THWN insulation is 380A and the rated temperature is
Thus, from Table 310.15(B)(2)(a), the correction factor of the ambient air temperature at
Thus, after correction, the ampacity will be
If a raceway is to contain more than three conductors, the ampacity of the conductors must be de-rated. The correction factors for six copper conductors is 80%. Thus, after correction, the ampacity will be
(f) From Table 310.15(B)(16), we know that the maximum ampacity of a 6 AWG copper conductor of Type THW-2 insulation is 75A and the rated temperature is
Thus, from Table 310.15(B)(2)(a), the correction factor of the ambient air temperature at
Thus, after correction, the ampacity will be
(g) From Table 310.15(B)(16), we know that the maximum ampacity of a 2/0 AWG aluminum conductor of Type UF insulation is 115A and the rated temperature is
Thus, from Table 310.15(B)(2)(a), the correction factor of the ambient air temperature at
Thus, after correction, the ampacity will be
If a raceway is to contain more than three conductors, the ampacity of the conductors must be de-rated. The correction factors for 12 aluminum conductors is 50%. Thus, after correction, the ampacity will be
(h) From Table 310.15(B)(16), we know that the maximum ampacity of a 750 kcmil aluminum conductor of Type RHW-2 insulation is 435A and the rated temperature is
Thus, from Table 310.15(B)(2)(a), the correction factor of the ambient air temperature at
Thus, after correction, the ampacity will be
If a raceway is to contain more than three conductors, the ampacity of the conductors must be de-rated. The correction factors for 6 aluminum conductors is 80%. Thus, after correction, the ampacity will be
Thus, the table will be:
Want to see more full solutions like this?
Chapter 11 Solutions
DELMAR'S STANDARD TEXT OF ELECTRICITY
- solve by impedancearrow_forwardConsider the circuit diagram below. Compute a single equivalent impedance for this circuit for a source frequency of F = 60 Hz. Express your final answer as a complex impedance with rectangular coordinates. You must show your all your work for the complex math. Include a diagram of the equivalent circuit as part of your solution.arrow_forwardConsider the circuit diagram below. Compute a single equivalent impedance for this circuit for a source frequency of f = 165 Hz. Express your final answer as a phasor with polar coordinates. You must show your all your work for the complex math. Include a diagram of the equivalent circuit as part of your solution.arrow_forward
- Consider the circuit diagram below. Using mesh analysis, compute the currents (a) IR1, (b) IL1, and (c) IC1. Express your final answers as phasors using polar coordinates with phase angles measured in degrees. Your solution should include the circuit diagram redrawn to indicate these currents and their directions. You must solve the system of equations using MATLAB and include the code or commands you ran as part of your solution.arrow_forwarduse kvl to solvearrow_forwardR1 is 978 ohms R2 is 2150 ohms R3 is 4780 R1 is parallel to R2 and R2 is parallel to R3 and R1 and R3 are in seriesarrow_forward
- Q7 For the circuit shown in Fig. 2.20, the transistors are identical and have the following parameters: hfe = 50, hie = 1.1K, hre = 0, and hoe = 0. Calculate Auf, Rif and Rof. Ans: 45.4; 112 KQ; 129. 25 V 10k 47k 4.7k Vo 150k w Vs 47k 4.7k W 22 5μF 33k 50uF 50μF 4.7k 4.7k R₁ Rof Rif R1000 Fig. 2.20 Circuit for Q7.arrow_forwardQ6)) The transistors in the feedback amplifier shown are identical, and their h-parameters are.. hie = 1.1k, hfe = 50, hre=o, and hoe = 0. Calculate Auf, Rif and Rof. {Ans: 6031583; 4. Kor. Is 4 4.7 k www 4.7k 91k 4.7k 91k 10k 1k. 10k 21000 4.7k w 15k Fig. 2.19 Circuit for Q6.arrow_forwardQ5 For the circuit shown in Fig. 2.18, hie =1.1 KQ, hfe =50. Find Avf, Rif and Rof Ans: -3.2; 193 ; 728 N. Vcc Vs Rs=10kQ Re=4KQ RF - = 40ΚΩ www Fig. 2.18 Circuit for Qs.arrow_forward
 Power System Analysis and Design (MindTap Course ...Electrical EngineeringISBN:9781305632134Author:J. Duncan Glover, Thomas Overbye, Mulukutla S. SarmaPublisher:Cengage Learning
Power System Analysis and Design (MindTap Course ...Electrical EngineeringISBN:9781305632134Author:J. Duncan Glover, Thomas Overbye, Mulukutla S. SarmaPublisher:Cengage Learning Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning
Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning

