USING+UNDERSTAND MATH W/MATHLABPLUS >I
15th Edition
ISBN: 9781269927116
Author: Bennett
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Question
Chapter 10.A, Problem 1QQ
To determine
Any two points can be used to define.
Expert Solution & Answer
Answer to Problem 1QQ
Solution:
Any two points can be used to define line.
Therefore, the correct option is (a)
Explanation of Solution
Through two points in a space, only a line can be drawn. A line is formed by connecting two points along the shortest possible path.
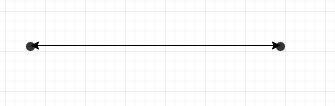Line
Conclusion:
With any two given point, a line can be drawn.
Want to see more full solutions like this?
Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Students have asked these similar questions
Answers
What is a solution to a differential equation? We said that a differential equation is an equation that
describes the derivative, or derivatives, of a function that is unknown to us. By a solution to a differential
equation, we mean simply a function that satisfies this description.
2. Here is a differential equation which describes an unknown position function s(t):
ds
dt
318
4t+1,
ds
(a) To check that s(t) = 2t2 + t is a solution to this differential equation, calculate
you really do get 4t +1.
and check that
dt'
(b) Is s(t) = 2t2 +++ 4 also a solution to this differential equation?
(c) Is s(t)=2t2 + 3t also a solution to this differential equation?
ds
1
dt
(d) To find all possible solutions, start with the differential equation = 4t + 1, then move dt to the
right side of the equation by multiplying, and then integrate both sides. What do you get?
(e) Does this differential equation have a unique solution, or an infinite family of solutions?
these are solutions to a tutorial that was done and im a little lost. can someone please explain to me how these iterations function, for example i Do not know how each set of matrices produces a number if someine could explain how its done and provide steps it would be greatly appreciated thanks.
Chapter 10 Solutions
USING+UNDERSTAND MATH W/MATHLABPLUS >I
Ch. 10.A - Prob. 1QQCh. 10.A - Prob. 2QQCh. 10.A - An acute angle is a. less than 90°. b. exactly...Ch. 10.A - 4. A regular polygon always has
a. four sides. b....Ch. 10.A - 5. A right triangle always has
three equal-length...Ch. 10.A - 6. The circumference of a circle of radius r...Ch. 10.A - The volume of a sphere of radius r is a. \[\pi...Ch. 10.A - Prob. 8QQCh. 10.A - If you triple the radius of a sphere, the volume...Ch. 10.A - Suppose you cut a large stone block into four...
Ch. 10.A - What do we mean by Euclidean geometry?Ch. 10.A - Prob. 2ECh. 10.A - What do we mean by dimension? How is dimension...Ch. 10.A - Prob. 4ECh. 10.A - What is plane geometry? What does it mean for...Ch. 10.A - 6. What is a polygon? How do we measure the...Ch. 10.A - What are the formulas for the circumference and...Ch. 10.A - 8. Describe how we calculate the volumes and...Ch. 10.A - What are the scaling laws for area and volume?...Ch. 10.A - Prob. 10ECh. 10.A - Prob. 11ECh. 10.A - Prob. 12ECh. 10.A - My bedroom is a rectangular prism that measures 12...Ch. 10.A - walked around the circular pond to a point on the...Ch. 10.A - Prob. 15ECh. 10.A - 16. By building a fence across my rectangular...Ch. 10.A - Prob. 17ECh. 10.A - Prob. 18ECh. 10.A - Angles and Circles. Find the degree measure of the...Ch. 10.A - 17-22: Angles and Circles. Find the degree measure...Ch. 10.A - 17-22: Angles and Circles. Find the degree measure...Ch. 10.A - 17-22: Angles and Circles. Find the degree measure...Ch. 10.A - Prob. 23ECh. 10.A - Prob. 24ECh. 10.A - Prob. 25ECh. 10.A - Prob. 26ECh. 10.A - Prob. 27ECh. 10.A - Prob. 28ECh. 10.A - Prob. 29ECh. 10.A - Prob. 30ECh. 10.A - Prob. 31ECh. 10.A - Prob. 32ECh. 10.A - Circle Practice. Find the circumference and area...Ch. 10.A - Prob. 34ECh. 10.A - Circle Practice. Find the circumference and area...Ch. 10.A - Prob. 36ECh. 10.A - Prob. 37ECh. 10.A - Prob. 38ECh. 10.A - Perimeters and Areas. Use Table 10.2 to find the...Ch. 10.A - Prob. 40ECh. 10.A - Prob. 41ECh. 10.A - Prob. 42ECh. 10.A - Triangle Geometry. Find the perimeter and area of...Ch. 10.A - Prob. 44ECh. 10.A - 43-46: Triangle Geometry. Find the perimeter and...Ch. 10.A - 43-46: Triangle Geometry. Find the perimeter and...Ch. 10.A - Window Space. A picture window has a length of 8...Ch. 10.A - A Running Track. A running track has straight legs...Ch. 10.A - Building Stairs. Refer to Figure 10.14, showing...Ch. 10.A - No Calculation Required. The end views of two...Ch. 10.A - Parking Lot. A parking lot is shaped like a...Ch. 10.A - Prob. 52ECh. 10.A - Prob. 53ECh. 10.A - Prob. 54ECh. 10.A - Three-Dimensional Objects. Use the formulas in...Ch. 10.A - Prob. 56ECh. 10.A - Prob. 57ECh. 10.A - 58. Water Canal. A water canal has a rectangular...Ch. 10.A - 59. Water Reservoir. The water reservoir for a...Ch. 10.A - 60. Oil Drums. Which holds more: an oil drum with...Ch. 10.A - Prob. 61ECh. 10.A - Architectural Model. Suppose you build an...Ch. 10.A - Architectural Model: Suppose you build an...Ch. 10.A - Prob. 64ECh. 10.A - Architectural Model: Suppose you build an...Ch. 10.A - Prob. 66ECh. 10.A - Architectural Model: Suppose you build an...Ch. 10.A - Prob. 68ECh. 10.A - Quadrupling Your Size. Suppose you magically...Ch. 10.A - Quadrupling Your Size. Suppose you magically...Ch. 10.A - Quadrupling Your Size. Suppose you magically...Ch. 10.A - 72-74: Comparing People. Consider a person named...Ch. 10.A - 72-74: Comparing People. Consider a person named...Ch. 10.A - Prob. 74ECh. 10.A - Squirrels or People? Squirrels and humans are both...Ch. 10.A - 75-76: Squirrels or People? Squirrels and humans...Ch. 10.A - Prob. 77ECh. 10.A - Prob. 78ECh. 10.A - Comparing Balls. Consider a softball with a radius...Ch. 10.A - Prob. 80ECh. 10.A - Dimension. Examine a closed book. How many...Ch. 10.A - Perpendicular and Parallel. Suppose you mark a...Ch. 10.A - Perpendicular and Parallel. Suppose you draw two...Ch. 10.A - Backyard. Figure 10.25 shows the layout of a...Ch. 10.A - Human Lung. The human lung has approximately 300...Ch. 10.A - 86. Automobile Engine Capacity. The size of a car...Ch. 10.A - Prob. 87ECh. 10.A - Prob. 88ECh. 10.A - Prob. 89ECh. 10.A - Prob. 90ECh. 10.A - The Geometry of Ancient Cultures. Research the use...Ch. 10.A - Surveying and GIS. Surveying is one of the oldest...Ch. 10.A - Platonic Solids. Why are there five and only five...Ch. 10.B - The number of minutes of are in a full circle is...Ch. 10.B - Prob. 2QQCh. 10.B - If you travel due east, you are traveling along a...Ch. 10.B - 4. If you are located at latitude 30°S and...Ch. 10.B - What would be different about the Sun if you...Ch. 10.B - Prob. 6QQCh. 10.B - If you are bicycling eastward up a hill with a 10%...Ch. 10.B - Prob. 8QQCh. 10.B - Prob. 9QQCh. 10.B - Prob. 10QQCh. 10.B - How do we describe fractions of a degree of angle?Ch. 10.B - Prob. 2ECh. 10.B - How is angular size related to physical size?Ch. 10.B - Prob. 4ECh. 10.B - Give at least two examples of ways in which the...Ch. 10.B - Prob. 6ECh. 10.B - Give an example of a practical problem that can be...Ch. 10.B - 8. What is an optimization problem? Give an...Ch. 10.B - 9. In December, it is winter at 70oW and 44oS.
Ch. 10.B - Prob. 10ECh. 10.B - Prob. 11ECh. 10.B - Prob. 12ECh. 10.B - Prob. 13ECh. 10.B - Prob. 14ECh. 10.B - Angle Conversions I. Convert the given degree...Ch. 10.B - 15-20: Angle Conversions I. Convert the given...Ch. 10.B - Prob. 17ECh. 10.B - Prob. 18ECh. 10.B - Prob. 19ECh. 10.B - Angle Conversions I. Convert the given degree...Ch. 10.B - 21-26: Angle Conversions II. Convert the given...Ch. 10.B - 21-26: Angle Conversions II. Convert the given...Ch. 10.B - Prob. 23ECh. 10.B - Prob. 24ECh. 10.B - Angle Conversions II. Convert the given angle...Ch. 10.B - Prob. 26ECh. 10.B - Prob. 27ECh. 10.B - Prob. 28ECh. 10.B - Prob. 29ECh. 10.B - Prob. 30ECh. 10.B - Prob. 31ECh. 10.B - Prob. 32ECh. 10.B - Prob. 33ECh. 10.B - Prob. 34ECh. 10.B - Prob. 35ECh. 10.B - Prob. 36ECh. 10.B - Angular Size. Use the formula relating angular...Ch. 10.B - Angular Size. Use the formula relating angular...Ch. 10.B - Angular Size. Use the formula relating angular...Ch. 10.B - Prob. 40ECh. 10.B - Prob. 41ECh. 10.B - Prob. 42ECh. 10.B - Prob. 43ECh. 10.B - Prob. 44ECh. 10.B - Prob. 45ECh. 10.B - 46. Grade of a Road. How much does a road with a...Ch. 10.B - 47. Pitch of a Roof. What is the angle (relative...Ch. 10.B - Grade of a Path. What is the approximate grade...Ch. 10.B - Prob. 49ECh. 10.B - Grade of a Trail. How much does a trail with a 22%...Ch. 10.B - Map Distances. Refer to the map in Figure 10.37....Ch. 10.B - Prob. 52ECh. 10.B - Prob. 53ECh. 10.B - Prob. 54ECh. 10.B - Prob. 55ECh. 10.B - Map Distances. Refer to the map in Figure 10.37....Ch. 10.B - Prob. 57ECh. 10.B - Prob. 58ECh. 10.B - 57-60: Acreage Problems. Refer to Figure 10.31,...Ch. 10.B - Acreage Problems. Refer to Figure 10.31, but use...Ch. 10.B - 61-64: Determining Similarity. Determine which...Ch. 10.B - Prob. 62ECh. 10.B - Prob. 63ECh. 10.B - Prob. 64ECh. 10.B - Prob. 65ECh. 10.B - Analyzing Similar Triangles. Determine the lengths...Ch. 10.B - Analyzing Similar Triangles. Determine the lengths...Ch. 10.B - Prob. 68ECh. 10.B - Solar Access. Assume that the policy given In...Ch. 10.B - Solar Access. Assume that the policy given In...Ch. 10.B - Solar Access. Assume that the policy given in...Ch. 10.B - Solar Access. Assume that the policy given in...Ch. 10.B - Prob. 73ECh. 10.B - Prob. 74ECh. 10.B - Prob. 75ECh. 10.B - Prob. 76ECh. 10.B - Prob. 77ECh. 10.B - Designing Plastic Buckets. A company manufactures...Ch. 10.B - Designing Cardboard Boxes. Suppose you are...Ch. 10.B - Designing Steel Safes. A large steel sale with a...Ch. 10.B - Blu-ray Geometry. The capacity of a single-sided,...Ch. 10.B - Prob. 82ECh. 10.B - Prob. 83ECh. 10.B - Prob. 84ECh. 10.B - Prob. 85ECh. 10.B - Prob. 86ECh. 10.B - Prob. 87ECh. 10.B - Filling a Pool. A spherical water tank has a...Ch. 10.B - Prob. 89ECh. 10.B - Prob. 90ECh. 10.B - Prob. 91ECh. 10.B - 92. Estimating Heights. In trying in estimate the...Ch. 10.B - 93. Soda Can Design. Standard soft drink cans hold...Ch. 10.B - 94. Melting Ice. A glaciers surface is...Ch. 10.B - Prob. 95ECh. 10.B - Prob. 96ECh. 10.B - Prob. 97ECh. 10.B - Prob. 98ECh. 10.B - Prob. 99ECh. 10.C - Fractal geometry is useful because it is the only...Ch. 10.C - Prob. 2QQCh. 10.C - Prob. 3QQCh. 10.C - Which of the following is a general characteristic...Ch. 10.C - How do fractal dimensions differ from in Euclidean...Ch. 10.C - 6. An island coastline has a fractal dimension...Ch. 10.C - Prob. 7QQCh. 10.C - Prob. 8QQCh. 10.C - Prob. 9QQCh. 10.C - Prob. 10QQCh. 10.C - Prob. 1ECh. 10.C - Prob. 2ECh. 10.C - Explain the meaning of the factors R and N used in...Ch. 10.C - What is the snowflake curve? Explain why we cannot...Ch. 10.C - Prob. 5ECh. 10.C - Prob. 6ECh. 10.C - Briefly describe what we mean by the process of...Ch. 10.C - 8. What is random iteration? Why do objects...Ch. 10.C - 9. I can use a yardstick to find the area of my...Ch. 10.C - I can use a yardstick to measure the length of the...Ch. 10.C - The area of the snowflake island is given by its...Ch. 10.C - Prob. 12ECh. 10.C - The edge of this leaf has a fractal dimension of...Ch. 10.C - This entire leaf, riddled with holes, has a...Ch. 10.C - Prob. 15ECh. 10.C - Prob. 16ECh. 10.C - Prob. 17ECh. 10.C - Prob. 18ECh. 10.C - Prob. 19ECh. 10.C - Prob. 20ECh. 10.C - 15-26: Ordinary and Fractal Dimensions. Find the...Ch. 10.C - 15-26: Ordinary and Fractal Dimensions. Find the...Ch. 10.C - 15-26: Ordinary and Fractal Dimensions. Find the...Ch. 10.C - Prob. 24ECh. 10.C - Prob. 25ECh. 10.C - Prob. 26ECh. 10.C - Prob. 27ECh. 10.C - Prob. 28ECh. 10.C - Prob. 29ECh. 10.C - Prob. 30ECh. 10.C - Prob. 31ECh. 10.C - Prob. 32ECh. 10.C - Prob. 33ECh. 10.C - Fractal Research. Locate at least two websites...Ch. 10.C - 35. Fractal Art. Visit a website that features...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Q1) Classify the following statements as a true or false statements a. Any ring with identity is a finitely generated right R module.- b. An ideal 22 is small ideal in Z c. A nontrivial direct summand of a module cannot be large or small submodule d. The sum of a finite family of small submodules of a module M is small in M A module M 0 is called directly indecomposable if and only if 0 and M are the only direct summands of M f. A monomorphism a: M-N is said to split if and only if Ker(a) is a direct- summand in M & Z₂ contains no minimal submodules h. Qz is a finitely generated module i. Every divisible Z-module is injective j. Every free module is a projective module Q4) Give an example and explain your claim in each case a) A module M which has two composition senes 7 b) A free subset of a modale c) A free module 24 d) A module contains a direct summand submodule 7, e) A short exact sequence of modules 74.arrow_forward************* ********************************* Q.1) Classify the following statements as a true or false statements: a. If M is a module, then every proper submodule of M is contained in a maximal submodule of M. b. The sum of a finite family of small submodules of a module M is small in M. c. Zz is directly indecomposable. d. An epimorphism a: M→ N is called solit iff Ker(a) is a direct summand in M. e. The Z-module has two composition series. Z 6Z f. Zz does not have a composition series. g. Any finitely generated module is a free module. h. If O→A MW→ 0 is short exact sequence then f is epimorphism. i. If f is a homomorphism then f-1 is also a homomorphism. Maximal C≤A if and only if is simple. Sup Q.4) Give an example and explain your claim in each case: Monomorphism not split. b) A finite free module. c) Semisimple module. d) A small submodule A of a module N and a homomorphism op: MN, but (A) is not small in M.arrow_forwardProve that Σ prime p≤x p=3 (mod 10) 1 Ρ = for some constant A. log log x + A+O 1 log x "arrow_forward
- Prove that, for x ≥ 2, d(n) n2 log x = B ― +0 X (금) n≤x where B is a constant that you should determine.arrow_forwardProve that, for x ≥ 2, > narrow_forwardI need diagram with solutionsarrow_forwardT. Determine the least common denominator and the domain for the 2x-3 10 problem: + x²+6x+8 x²+x-12 3 2x 2. Add: + Simplify and 5x+10 x²-2x-8 state the domain. 7 3. Add/Subtract: x+2 1 + x+6 2x+2 4 Simplify and state the domain. x+1 4 4. Subtract: - Simplify 3x-3 x²-3x+2 and state the domain. 1 15 3x-5 5. Add/Subtract: + 2 2x-14 x²-7x Simplify and state the domain.arrow_forwardQ.1) Classify the following statements as a true or false statements: Q a. A simple ring R is simple as a right R-module. b. Every ideal of ZZ is small ideal. very den to is lovaginz c. A nontrivial direct summand of a module cannot be large or small submodule. d. The sum of a finite family of small submodules of a module M is small in M. e. The direct product of a finite family of projective modules is projective f. The sum of a finite family of large submodules of a module M is large in M. g. Zz contains no minimal submodules. h. Qz has no minimal and no maximal submodules. i. Every divisible Z-module is injective. j. Every projective module is a free module. a homomorp cements Q.4) Give an example and explain your claim in each case: a) A module M which has a largest proper submodule, is directly indecomposable. b) A free subset of a module. c) A finite free module. d) A module contains no a direct summand. e) A short split exact sequence of modules.arrow_forward1 2 21. For the matrix A = 3 4 find AT (the transpose of A). 22. Determine whether the vector @ 1 3 2 is perpendicular to -6 3 2 23. If v1 = (2) 3 and v2 = compute V1 V2 (dot product). .arrow_forward7. Find the eigenvalues of the matrix (69) 8. Determine whether the vector (£) 23 is in the span of the vectors -0-0 and 2 2arrow_forward1. Solve for x: 2. Simplify: 2x+5=15. (x+3)² − (x − 2)². - b 3. If a = 3 and 6 = 4, find (a + b)² − (a² + b²). 4. Solve for x in 3x² - 12 = 0. -arrow_forward5. Find the derivative of f(x) = 6. Evaluate the integral: 3x3 2x²+x— 5. - [dz. x² dx.arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education
Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON
Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning,
Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education
Discrete Mathematics and Its Applications ( 8th I...
Math
ISBN:9781259676512
Author:Kenneth H Rosen
Publisher:McGraw-Hill Education
Mathematics for Elementary Teachers with Activiti...
Math
ISBN:9780134392790
Author:Beckmann, Sybilla
Publisher:PEARSON
Thinking Mathematically (7th Edition)
Math
ISBN:9780134683713
Author:Robert F. Blitzer
Publisher:PEARSON
Discrete Mathematics With Applications
Math
ISBN:9781337694193
Author:EPP, Susanna S.
Publisher:Cengage Learning,
Pathways To Math Literacy (looseleaf)
Math
ISBN:9781259985607
Author:David Sobecki Professor, Brian A. Mercer
Publisher:McGraw-Hill Education
Points, Lines, Planes, Segments, & Rays - Collinear vs Coplanar Points - Geometry; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=dDWjhRfBsKM;License: Standard YouTube License, CC-BY
Naming Points, Lines, and Planes; Author: Florida PASS Program;https://www.youtube.com/watch?v=F-LxiLSSaLg;License: Standard YouTube License, CC-BY