Chapter 10.6, Problem 53E

How would you like to live to be 200 years old? For centuries, humankind has sought the key to the mystery of aging. What causes aging? How can aging be slowed? Studies have focused on biomarkers, physical or biological changes that occur at a predictable time in a person’s life. The theory is that, if ways can be found to delay the occurrence of these biomarkers, human life can be extended. A key biomarker, according to scientists, is forced vital capacity (FVC), the volume of air that a person can expel after taking a deep breath. A study of 5209 men and women aged 30 to 62 showed that FVC declined, on the average, 3.8 deciliters (dl) per decade for men and 3.1 deciliters per decade for women.¹⁰ Suppose that you wished to determine whether a physical fitness program for men and women aged 50 to 60 would delay aging: to do so, you measured the FVC for 30 men and 30 women participating in the fitness program at the beginning and end of the 50-to 60-year age interval and recorded the drop in FVC for each person. A summary of the data appears in the accompanying table.

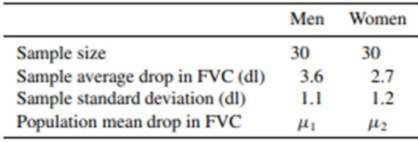
1. a Do the data provide sufficient evidence to indicate that the decrease in the mean FVC over the decade for the men on the physical fitness program is less than 3.8 dl? Find the attained significance level for the test.
2. b Refer to part (a). If you choose α = .05, do the data support the contention that the mean decrease in FVC is less titan 3.8 dl?
3. c Test to determine whether the FVC drop for women on the physical fitness program was less than 3.1 dl for the decade. Find the attained significance level for the test.
4. d Refer to part (c). If you choose α = .05, do the data support the contention that the mean decrease in FVC is less than 3.1 dl?