Algebra and Trigonometry (6th Edition)
6th Edition
ISBN: 9780134463216
Author: Robert F. Blitzer
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 10.5, Problem 70E
The path of a projectile that is launched h feet above the ground with an initial velocity of t\) feet per second and at an angle 0 with the horizontal is given by the parametric equations
where t is the time, in seconds, after the projectile was launched. The parametric equation for x gives the projectile’s horizontal distance, in feet. The parametric equation for y gives the projectile’s| height, in feet. Use these parametric equations to solve Exercises 69 -70.
The figure shows the path for a baseball that was hit with an initial velocity of 150 feet per second at an angle of 35° to the horizontal. The ball was hit at a height of 3 feet off the ground.
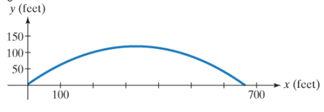
a. Find the parametric equations that describe the position of the ball as a function of time.
b. Describe the ball's position after 1, 2, and 3 seconds. Round to the nearest tenth of a foot. Locate your solutions on the plane curve.
c. How long is the ball in flight? (Round to the nearest tenth of a second. ) What is the total horizontal distance that it travels, to the nearest tenth of a foot, before it lands? Is your answer consistent with the figure shown?
d. Use the graph to describe something about the path of the baseball that might be of interest to the player who hit the ball. Then verify your observation algebraically.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
For each graph below, state whether it represents a function.
Graph 1
24y
Graph 2
Graph 3
4
2
-8
-6 -4
-2
-2
2 4 6
Function?
○ Yes
○ No
○ Yes
○ No
Graph 4
Graph 5
8
Function?
Yes
No
Yes
No
-2.
○ Yes
○ No
Graph 6
4
+
2
4
-8 -6 -4 -2
2 4 6
8
Yes
-4++
No
Practice
k Help
ises
A
96
Anewer The probability that you get a sum of at least 10 is
Determine the number of ways that the specified event can occur when
two number cubes are rolled.
1. Getting a sum of 9 or 10
3. Getting a sum less than 5
2. Getting a sum of 6 or 7
4. Getting a sum that is odd
Tell whether you would use the addition principle or the multiplication
principle to determine the total number of possible outcomes for the
situation described.
5. Rolling three number cubes
6. Getting a sum of 10 or 12 after rolling three number cubes
A set of playing cards contains four groups of cards designated by color
(black, red, yellow, and green) with cards numbered from 1 to 14 in each
group. Determine the number of ways that the specified event can occur
when a card is drawn from the set.
7. Drawing a 13 or 14
9. Drawing a number less than 4
8. Drawing a yellow or green card
10. Drawing a black, red, or green car
The spinner is divided into equal parts.
Find the specified…
Answer the questions
Chapter 10 Solutions
Algebra and Trigonometry (6th Edition)
Ch. 10.1 - Fill in each blank so that the resulting statement...Ch. 10.1 - Prob. 2CVCCh. 10.1 - Prob. 3CVCCh. 10.1 - Prob. 4CVCCh. 10.1 - The graph of (x+1)225+(y4)29=1 has its center...Ch. 10.1 - Prob. 6CVCCh. 10.1 - Prob. 7CVCCh. 10.1 - 8. In the equation , we complete the square on x...Ch. 10.1 - In Exercises 1-18, graph each ellipse and locate...Ch. 10.1 - Prob. 2E
Ch. 10.1 - In Exercises 1-18, graph each ellipse and locate...Ch. 10.1 - In Exercises 1-18, graph each ellipse and locate...Ch. 10.1 - In Exercises 1-18, graph each ellipse and locate...Ch. 10.1 - In Exercises 1-18, graph each ellipse and locate...Ch. 10.1 - In Exercises 1-18, graph each ellipse and locate...Ch. 10.1 - In Exercises 1-18, graph each ellipse and locate...Ch. 10.1 - In Exercises 1-18, graph each ellipse and locate...Ch. 10.1 - In Exercises 1-18, graph each ellipse and locate...Ch. 10.1 - In Exercises 1-18, graph each ellipse and locate...Ch. 10.1 - In Exercises 1-18, graph each ellipse and locate...Ch. 10.1 - In Exercises 1-18, graph each ellipse and locate...Ch. 10.1 - In Exercises 1-18, graph each ellipse and locate...Ch. 10.1 - In Exercises 1-18, graph each ellipse and locate...Ch. 10.1 - In Exercises 1-18, graph each ellipse and locate...Ch. 10.1 - In Exercises 1-18, graph each ellipse and locate...Ch. 10.1 - In Exercises 1-18, graph each ellipse and locate...Ch. 10.1 - In Exercises 19-24, find the standard form of the...Ch. 10.1 - In Exercises 19-24, find the standard form of the...Ch. 10.1 - Prob. 21ECh. 10.1 - Prob. 22ECh. 10.1 - Prob. 23ECh. 10.1 - Prob. 24ECh. 10.1 - Prob. 25ECh. 10.1 - Prob. 26ECh. 10.1 - Prob. 27ECh. 10.1 - Prob. 28ECh. 10.1 - Prob. 29ECh. 10.1 - Prob. 30ECh. 10.1 - Prob. 31ECh. 10.1 - Prob. 32ECh. 10.1 - Prob. 33ECh. 10.1 - Prob. 34ECh. 10.1 - Prob. 35ECh. 10.1 - Prob. 36ECh. 10.1 - Prob. 37ECh. 10.1 - Prob. 38ECh. 10.1 - Prob. 39ECh. 10.1 - Prob. 40ECh. 10.1 - Prob. 41ECh. 10.1 - Prob. 42ECh. 10.1 - Prob. 43ECh. 10.1 - Prob. 44ECh. 10.1 - Prob. 45ECh. 10.1 - Prob. 46ECh. 10.1 - Prob. 47ECh. 10.1 - Prob. 48ECh. 10.1 - Prob. 49ECh. 10.1 - Prob. 50ECh. 10.1 - Prob. 51ECh. 10.1 - Prob. 52ECh. 10.1 - Prob. 53ECh. 10.1 - In Exercises 51-60, convert each equation to...Ch. 10.1 - Prob. 55ECh. 10.1 - Prob. 56ECh. 10.1 - Prob. 57ECh. 10.1 - Prob. 58ECh. 10.1 - Prob. 59ECh. 10.1 - Prob. 60ECh. 10.1 - Prob. 61ECh. 10.1 - Prob. 62ECh. 10.1 - Prob. 63ECh. 10.1 - Prob. 64ECh. 10.1 - Prob. 65ECh. 10.1 - Prob. 66ECh. 10.1 - Prob. 67ECh. 10.1 - Prob. 68ECh. 10.1 - Prob. 69ECh. 10.1 - Prob. 70ECh. 10.1 - The elliptical ceiling in Statuary Hall in the...Ch. 10.1 - Prob. 72ECh. 10.1 - Prob. 73ECh. 10.1 - Prob. 74ECh. 10.1 - Prob. 75ECh. 10.1 - Prob. 76ECh. 10.1 - Prob. 77ECh. 10.1 - Prob. 78ECh. 10.1 - Prob. 79ECh. 10.1 - Prob. 80ECh. 10.1 - Prob. 81ECh. 10.1 - 82. Write an equation for the path of each of the...Ch. 10.1 - Make Sense? In Exercises 83-86, determine whether...Ch. 10.1 - Prob. 84ECh. 10.1 - Prob. 85ECh. 10.1 - Prob. 86ECh. 10.1 - Prob. 87ECh. 10.1 - Prob. 88ECh. 10.1 - Prob. 89ECh. 10.1 - Prob. 90ECh. 10.1 - Prob. 91ECh. 10.1 - Prob. 92ECh. 10.1 - Prob. 93ECh. 10.1 - Prob. 94ECh. 10.1 - Prob. 95ECh. 10.1 - Prob. 96ECh. 10.1 - Exercises 95-97 will help you prepare for the...Ch. 10.2 - Fill in each blank so that the resulting statement...Ch. 10.2 - Prob. 2CVCCh. 10.2 - Prob. 3CVCCh. 10.2 - Prob. 4CVCCh. 10.2 - Prob. 5CVCCh. 10.2 - Prob. 6CVCCh. 10.2 - Prob. 7CVCCh. 10.2 - Prob. 8CVCCh. 10.2 - Prob. 9CVCCh. 10.2 - Prob. 10CVCCh. 10.2 - In Exercises 1-4, find the vertices and locate the...Ch. 10.2 - Prob. 2ECh. 10.2 - Prob. 3ECh. 10.2 - Prob. 4ECh. 10.2 - Prob. 5ECh. 10.2 - Prob. 6ECh. 10.2 - Prob. 7ECh. 10.2 - Prob. 8ECh. 10.2 - In Exercises 5-12, find the standard form of the...Ch. 10.2 - Prob. 10ECh. 10.2 - Prob. 11ECh. 10.2 - In Exercises 5-12, find the standard form of the...Ch. 10.2 - Prob. 13ECh. 10.2 - Prob. 14ECh. 10.2 - Prob. 15ECh. 10.2 - In Exercises 13-26, use vertices and asymptotes to...Ch. 10.2 - Prob. 17ECh. 10.2 - Prob. 18ECh. 10.2 - Prob. 19ECh. 10.2 - Prob. 20ECh. 10.2 - Prob. 21ECh. 10.2 - Prob. 22ECh. 10.2 - Prob. 23ECh. 10.2 - Prob. 24ECh. 10.2 - Prob. 25ECh. 10.2 - Prob. 26ECh. 10.2 - Prob. 27ECh. 10.2 - Prob. 28ECh. 10.2 - Prob. 29ECh. 10.2 - Prob. 30ECh. 10.2 - Prob. 31ECh. 10.2 - Prob. 32ECh. 10.2 - Prob. 33ECh. 10.2 - Prob. 34ECh. 10.2 - Prob. 35ECh. 10.2 - Prob. 36ECh. 10.2 - Prob. 37ECh. 10.2 - Prob. 38ECh. 10.2 - In Exercises 33—42, use the center, vertices, and...Ch. 10.2 - Prob. 40ECh. 10.2 - In Exercises 33—42, use the center, vertices, and...Ch. 10.2 - Prob. 42ECh. 10.2 - Prob. 43ECh. 10.2 - Prob. 44ECh. 10.2 - Prob. 45ECh. 10.2 - In Exercises -43-50, convert each equation to...Ch. 10.2 - Prob. 47ECh. 10.2 - Prob. 48ECh. 10.2 - Prob. 49ECh. 10.2 - Prob. 50ECh. 10.2 - Prob. 51ECh. 10.2 - Prob. 52ECh. 10.2 - Prob. 53ECh. 10.2 - Prob. 54ECh. 10.2 - Prob. 55ECh. 10.2 - Prob. 56ECh. 10.2 - Prob. 57ECh. 10.2 - Prob. 58ECh. 10.2 - Prob. 59ECh. 10.2 - Prob. 60ECh. 10.2 - 61. An explosion is recorded by two microphones...Ch. 10.2 - Radio lowers A and B. 200 kilometers apart, are...Ch. 10.2 - Prob. 63ECh. 10.2 - Prob. 64ECh. 10.2 - Prob. 65ECh. 10.2 - Prob. 66ECh. 10.2 - Prob. 67ECh. 10.2 - Prob. 68ECh. 10.2 - Prob. 69ECh. 10.2 - Prob. 70ECh. 10.2 - Prob. 71ECh. 10.2 - Prob. 72ECh. 10.2 - Prob. 73ECh. 10.2 - Prob. 74ECh. 10.2 - Prob. 75ECh. 10.2 - Prob. 76ECh. 10.2 - Prob. 77ECh. 10.2 - Prob. 78ECh. 10.2 - Prob. 79ECh. 10.2 - Prob. 80ECh. 10.2 - Prob. 81ECh. 10.2 - I noticed that the definition of a hyperbola...Ch. 10.2 - Prob. 83ECh. 10.2 - Prob. 84ECh. 10.2 - Prob. 85ECh. 10.2 - In Exercises 85-88, determine whether each...Ch. 10.2 - Prob. 87ECh. 10.2 - Prob. 88ECh. 10.2 - Prob. 89ECh. 10.2 - Prob. 90ECh. 10.2 - Prob. 91ECh. 10.2 - Prob. 92ECh. 10.2 - Prob. 93ECh. 10.2 - Prob. 94ECh. 10.2 - Prob. 95ECh. 10.2 - Prob. 96ECh. 10.2 - Prob. 97ECh. 10.2 - Prob. 98ECh. 10.3 - The set of all points in a plane that are...Ch. 10.3 - Prob. 2CVCCh. 10.3 - Use the graph shown to answer Exercises 2-5. If...Ch. 10.3 - Prob. 4CVCCh. 10.3 - Use the graph shown to answer Exercises 2-5. If...Ch. 10.3 - Use the graph shown lo answer Exercises 6-9.
6....Ch. 10.3 - Prob. 7CVCCh. 10.3 - Use the graph shown to answer Exercises 6-9. If...Ch. 10.3 - Use the graph shown to answer Exercises 6-9. If...Ch. 10.3 - Prob. 10CVCCh. 10.3 - In Exercises 1-4, find the focus and directrix of...Ch. 10.3 - Prob. 2ECh. 10.3 - Prob. 3ECh. 10.3 - Prob. 4ECh. 10.3 - Prob. 5ECh. 10.3 - Prob. 6ECh. 10.3 - Prob. 7ECh. 10.3 - Prob. 8ECh. 10.3 - Prob. 9ECh. 10.3 - Prob. 10ECh. 10.3 - Prob. 11ECh. 10.3 - Prob. 12ECh. 10.3 - Prob. 13ECh. 10.3 - Prob. 14ECh. 10.3 - Prob. 15ECh. 10.3 - Prob. 16ECh. 10.3 - In Exercises 17-30, find the standard form of the...Ch. 10.3 - Prob. 18ECh. 10.3 - Prob. 19ECh. 10.3 - Prob. 20ECh. 10.3 - Prob. 21ECh. 10.3 - Prob. 22ECh. 10.3 - Prob. 23ECh. 10.3 - Prob. 24ECh. 10.3 - Prob. 25ECh. 10.3 - Prob. 26ECh. 10.3 - Prob. 27ECh. 10.3 - Prob. 28ECh. 10.3 - Prob. 29ECh. 10.3 - Prob. 30ECh. 10.3 - Prob. 31ECh. 10.3 - Prob. 32ECh. 10.3 - Prob. 33ECh. 10.3 - Prob. 34ECh. 10.3 - Prob. 35ECh. 10.3 - Prob. 36ECh. 10.3 - Prob. 37ECh. 10.3 - Prob. 38ECh. 10.3 - Prob. 39ECh. 10.3 - Prob. 40ECh. 10.3 - Prob. 41ECh. 10.3 - Prob. 42ECh. 10.3 - Prob. 43ECh. 10.3 - Prob. 44ECh. 10.3 - Prob. 45ECh. 10.3 - Prob. 46ECh. 10.3 - Prob. 47ECh. 10.3 - Prob. 48ECh. 10.3 - Prob. 49ECh. 10.3 - Prob. 50ECh. 10.3 - Prob. 51ECh. 10.3 - Prob. 52ECh. 10.3 - Prob. 53ECh. 10.3 - Prob. 54ECh. 10.3 - Prob. 55ECh. 10.3 - Prob. 56ECh. 10.3 - Prob. 57ECh. 10.3 - Prob. 58ECh. 10.3 - Prob. 59ECh. 10.3 - Prob. 60ECh. 10.3 - Prob. 61ECh. 10.3 - In Exercises 57-62, use the vertex and the...Ch. 10.3 - Prob. 63ECh. 10.3 - Prob. 64ECh. 10.3 - Prob. 65ECh. 10.3 - Prob. 66ECh. 10.3 - Prob. 67ECh. 10.3 - Prob. 68ECh. 10.3 - Prob. 69ECh. 10.3 - Prob. 70ECh. 10.3 - Prob. 71ECh. 10.3 - Prob. 72ECh. 10.3 - Prob. 73ECh. 10.3 - 74. The towers of a suspension bridge are 800 feet...Ch. 10.3 - Prob. 75ECh. 10.3 - Prob. 76ECh. 10.3 - Prob. 77ECh. 10.3 - Prob. 78ECh. 10.3 - Prob. 79ECh. 10.3 - 80. Describe one similarity and one difference...Ch. 10.3 - Prob. 81ECh. 10.3 - Prob. 82ECh. 10.3 - Prob. 83ECh. 10.3 - Prob. 84ECh. 10.3 - Prob. 85ECh. 10.3 - Prob. 86ECh. 10.3 - Prob. 87ECh. 10.3 - Prob. 88ECh. 10.3 - Prob. 89ECh. 10.3 - Make Sense? In Exercises 90-93. determine whether...Ch. 10.3 - Prob. 91ECh. 10.3 - Prob. 92ECh. 10.3 - Prob. 93ECh. 10.3 - Prob. 94ECh. 10.3 - Prob. 95ECh. 10.3 - Prob. 96ECh. 10.3 - Prob. 97ECh. 10.3 - Prob. 98ECh. 10.3 - Prob. 99ECh. 10.3 - Prob. 100ECh. 10.3 - Prob. 101ECh. 10.3 - Prob. 102ECh. 10.3 - Prob. 103ECh. 10.3 - Prob. 104ECh. 10.3 - Prob. 105ECh. 10.3 - Prob. 106ECh. 10.3 - Prob. 107ECh. 10.4 - Prob. 1CVCCh. 10.4 - Prob. 2CVCCh. 10.4 - Prob. 1ECh. 10.4 - Prob. 2ECh. 10.4 - Prob. 3ECh. 10.4 - Prob. 4ECh. 10.4 - Prob. 5ECh. 10.4 - Prob. 6ECh. 10.4 - Prob. 7ECh. 10.4 - Prob. 8ECh. 10.4 - Prob. 9ECh. 10.4 - Prob. 10ECh. 10.4 - Prob. 11ECh. 10.4 - Prob. 12ECh. 10.4 - In Exercises 7-18, write the appropriate rotation...Ch. 10.4 - Prob. 14ECh. 10.4 - Prob. 15ECh. 10.4 - Prob. 16ECh. 10.4 - Prob. 17ECh. 10.4 - Prob. 18ECh. 10.4 - Prob. 19ECh. 10.4 - Prob. 20ECh. 10.4 - Prob. 21ECh. 10.4 - Prob. 22ECh. 10.4 - Prob. 23ECh. 10.4 - Prob. 24ECh. 10.4 - Prob. 25ECh. 10.4 - Prob. 26ECh. 10.4 - Prob. 27ECh. 10.4 - Prob. 28ECh. 10.4 - Prob. 29ECh. 10.4 - Prob. 30ECh. 10.4 - Prob. 31ECh. 10.4 - Prob. 32ECh. 10.4 - Prob. 33ECh. 10.4 - Prob. 34ECh. 10.4 - Prob. 35ECh. 10.4 - In Exercises 31-36.identify each equation without...Ch. 10.4 - In Exercises 37-40,
• If the graph of the equation...Ch. 10.4 - Prob. 38ECh. 10.4 - In Exercises 37-40, If the graph of the equation...Ch. 10.4 - In Exercises 37-40. If the graph of the equation...Ch. 10.4 - Prob. 41ECh. 10.4 - Prob. 42ECh. 10.4 - Prob. 43ECh. 10.4 - Prob. 44ECh. 10.4 - Prob. 45ECh. 10.4 - Prob. 46ECh. 10.4 - Prob. 47ECh. 10.4 - Prob. 48ECh. 10.4 - Prob. 49ECh. 10.4 - Prob. 50ECh. 10.4 - Prob. 51ECh. 10.4 - Prob. 52ECh. 10.4 - Prob. 53ECh. 10.4 - Prob. 54ECh. 10.4 - Prob. 55ECh. 10.4 - Prob. 56ECh. 10.4 - Prob. 57ECh. 10.4 - In Exercises 58 -59, let Ax2+Bxy+Cy2+Dx+Ey+F=0 be...Ch. 10.4 - Prob. 59ECh. 10.4 - Prob. 60ECh. 10.4 - Prob. 61ECh. 10.4 - Prob. 62ECh. 10.4 - Prob. 63ECh. 10.4 - Prob. 64ECh. 10.4 - Prob. 65ECh. 10.4 - Prob. 66ECh. 10.5 - Prob. 1CVCCh. 10.5 - Prob. 2CVCCh. 10.5 - Prob. 3CVCCh. 10.5 - Prob. 4CVCCh. 10.5 - Prob. 1ECh. 10.5 - Prob. 2ECh. 10.5 - Prob. 3ECh. 10.5 - Prob. 4ECh. 10.5 - Prob. 5ECh. 10.5 - Prob. 6ECh. 10.5 - Prob. 7ECh. 10.5 - Prob. 8ECh. 10.5 - Prob. 9ECh. 10.5 - Prob. 10ECh. 10.5 - Prob. 11ECh. 10.5 - Prob. 12ECh. 10.5 - Prob. 13ECh. 10.5 - Prob. 14ECh. 10.5 - Prob. 15ECh. 10.5 - Prob. 16ECh. 10.5 - Prob. 17ECh. 10.5 - Prob. 18ECh. 10.5 - Prob. 19ECh. 10.5 - Prob. 20ECh. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - Prob. 41ECh. 10.5 - Prob. 42ECh. 10.5 - Prob. 43ECh. 10.5 - Prob. 44ECh. 10.5 - Prob. 45ECh. 10.5 - Prob. 46ECh. 10.5 - Prob. 47ECh. 10.5 - Prob. 48ECh. 10.5 - Prob. 49ECh. 10.5 - Prob. 50ECh. 10.5 - Prob. 51ECh. 10.5 - Prob. 52ECh. 10.5 - Prob. 53ECh. 10.5 - Prob. 54ECh. 10.5 - Prob. 55ECh. 10.5 - Prob. 56ECh. 10.5 - Prob. 57ECh. 10.5 - Prob. 58ECh. 10.5 - Prob. 59ECh. 10.5 - Prob. 60ECh. 10.5 - Prob. 61ECh. 10.5 - Prob. 62ECh. 10.5 - Prob. 63ECh. 10.5 - In Exercises 63-68, sketch the function...Ch. 10.5 - In Exercises 63-68, sketch the function...Ch. 10.5 - Prob. 66ECh. 10.5 - Prob. 67ECh. 10.5 - Prob. 68ECh. 10.5 - Prob. 69ECh. 10.5 - The path of a projectile that is launched h feet...Ch. 10.5 - Prob. 71ECh. 10.5 - Prob. 72ECh. 10.5 - What is the significance of arrows along a plane...Ch. 10.5 - Prob. 74ECh. 10.5 - Prob. 75ECh. 10.5 - Prob. 76ECh. 10.5 - Prob. 77ECh. 10.5 - Prob. 78ECh. 10.5 - Prob. 79ECh. 10.5 - Prob. 80ECh. 10.5 - Prob. 81ECh. 10.5 - Prob. 82ECh. 10.5 - In Exercises 83-84, use a graphing utility to...Ch. 10.5 - Prob. 84ECh. 10.5 - Prob. 85ECh. 10.5 - Prob. 86ECh. 10.5 - Prob. 87ECh. 10.5 - Prob. 88ECh. 10.5 - Prob. 89ECh. 10.5 - Prob. 90ECh. 10.5 - Prob. 91ECh. 10.5 - Prob. 92ECh. 10.5 - Find all zeros of f(x)=2x3+2x213x+6. (Section 3.4,...Ch. 10.5 - Prob. 94ECh. 10.5 - Prob. 95ECh. 10.5 - Prob. 96ECh. 10.5 - Prob. 97ECh. 10.5 - Prob. 98ECh. 10.5 - Prob. 99ECh. 10.6 - Prob. 1CVCCh. 10.6 - Prob. 2CVCCh. 10.6 - Fill in each blank so that the resulting statement...Ch. 10.6 - Fill in each blank so that the resulting statement...Ch. 10.6 - Fill in each blank so that the resulting statement...Ch. 10.6 - Prob. 1ECh. 10.6 - Prob. 2ECh. 10.6 - Prob. 3ECh. 10.6 - Prob. 4ECh. 10.6 - Prob. 5ECh. 10.6 - Prob. 6ECh. 10.6 - Prob. 7ECh. 10.6 - Prob. 8ECh. 10.6 - Prob. 9ECh. 10.6 - Prob. 10ECh. 10.6 - Prob. 11ECh. 10.6 - Prob. 12ECh. 10.6 - Prob. 13ECh. 10.6 - Prob. 14ECh. 10.6 - Prob. 15ECh. 10.6 - Prob. 16ECh. 10.6 - Prob. 17ECh. 10.6 - Prob. 18ECh. 10.6 - Prob. 19ECh. 10.6 - Prob. 20ECh. 10.6 - Prob. 21ECh. 10.6 - Prob. 22ECh. 10.6 - Prob. 23ECh. 10.6 - Prob. 24ECh. 10.6 - Prob. 25ECh. 10.6 - Prob. 26ECh. 10.6 - Prob. 27ECh. 10.6 - In Exercises 21 -28 , describe a viewing...Ch. 10.6 - Halley's Cornel has an elliptical orbit with the...Ch. 10.6 - Prob. 30ECh. 10.6 - On February 20,1962, John Glenn made the first...Ch. 10.6 - On February 20, 1962, John Glenn made the first...Ch. 10.6 - Prob. 33ECh. 10.6 - Prob. 34ECh. 10.6 - Prob. 35ECh. 10.6 - Prob. 36ECh. 10.6 - Describe a strategy for graphing r=11+sin.Ch. 10.6 - You meet an astronaut and she asks you to tell her...Ch. 10.6 - Use the polar mode of a graphing utility with...Ch. 10.6 - Prob. 40ECh. 10.6 - Prob. 41ECh. 10.6 - Prob. 42ECh. 10.6 - Prob. 43ECh. 10.6 - Prob. 44ECh. 10.6 - Prob. 45ECh. 10.6 - Make Sense? In Exercises 46-49, determine whether...Ch. 10.6 - Prob. 47ECh. 10.6 - Prob. 48ECh. 10.6 - Prob. 49ECh. 10.6 - Prob. 50ECh. 10.6 - In Exercises 51-52, write a polar equation of the...Ch. 10.6 - In Exercises 51-52, write a polar equation of the...Ch. 10.6 - Prob. 53ECh. 10.6 - Prob. 54ECh. 10.6 - 55. Expand: (Section 4.3, Example 4)
Ch. 10.6 - Solve the system: { x+y=1x2+y2=25 (Section 8.4,...Ch. 10.6 - 57. Verify the identity:
...Ch. 10.6 - Two fire-lookout stations are 10 miles apart with...Ch. 10.6 - Exercises 59-61 will help you prepare for the...Ch. 10.6 - Exercises 59-61 will help you prepare for the...Ch. 10.6 - Exercises 59-61 will help you prepare for the...Ch. 10 - In Exercises 1-5, graph each ellipse. Give the...Ch. 10 - Prob. 2MCCPCh. 10 - Prob. 3MCCPCh. 10 - Prob. 4MCCPCh. 10 - Prob. 5MCCPCh. 10 - In Exercises 6-11, graph each hyperbola. Give the...Ch. 10 - In Exercises 6-11, graph each hyperbola. Give the...Ch. 10 - In Exercises 6-11, graph each hyperbola. Give the...Ch. 10 - In Exercises 6-11, graph each hyperbola. Give the...Ch. 10 - In Exercises 6-11. graph each hyperbola. Give the...Ch. 10 - In Exercises 6-11, graph each hyperbola. Give the...Ch. 10 - In Exercises 12-13 , graph each parabola. Give the...Ch. 10 - In Exercises 12-13 . graph each parabola. Give the...Ch. 10 - In Exercises 14-16, identify each equation without...Ch. 10 - In Exercises 14-16, identify each equation without...Ch. 10 - In Exercises 14-16, identify each equation without...Ch. 10 - In Exercises 17-24, graph each equation. x2+y2=4Ch. 10 - In Exercises 17-24, graph each equation.
18.
Ch. 10 - In Exercises 17-24, graph each equation.
19.
Ch. 10 - In Exercises 17-24, graph each equation.
20.
Ch. 10 - In Exercises 17-24, graph each equation.
21.
Ch. 10 - In Exercises 17-24, graph each equation.
22.
Ch. 10 - In Exercises 17-24, graph each equation....Ch. 10 - In Exercises 17-24, graph each equation....Ch. 10 - Prob. 25MCCPCh. 10 - In Exercises 25-30, find the standard form of the...Ch. 10 - Prob. 27MCCPCh. 10 - Prob. 28MCCPCh. 10 - In Exercises 25-30, find the standdpd form of the...Ch. 10 - In Exercises 25-30, find the standard form of the...Ch. 10 - A semielliptical archway over a one-way road has a...Ch. 10 - A lithotriper is used to disentegrate kidney...Ch. 10 - 33. An explosion is recorded by two forest...Ch. 10 - A domed ceiling is a parabolic surface. Ten meters...Ch. 10 - In Exercises 1-8, graph each ellipse and locate...Ch. 10 - Prob. 2RECh. 10 - In Exercises 1-8, graph each ellipse and locate...Ch. 10 - Prob. 4RECh. 10 - Prob. 5RECh. 10 - Prob. 6RECh. 10 - Prob. 7RECh. 10 - Prob. 8RECh. 10 - Prob. 9RECh. 10 - Prob. 10RECh. 10 - Prob. 11RECh. 10 - Prob. 12RECh. 10 - Prob. 13RECh. 10 - Prob. 14RECh. 10 - Prob. 15RECh. 10 - Prob. 16RECh. 10 - Prob. 17RECh. 10 - Prob. 18RECh. 10 - Prob. 19RECh. 10 - Prob. 20RECh. 10 - In Exercises 15-22, graph each hyperbula. Locate...Ch. 10 - In Exercises 15-22, graph each hyperbola. Locate...Ch. 10 - Prob. 23RECh. 10 - Prob. 24RECh. 10 - 25. Explain why it is not possible for a hyperbola...Ch. 10 - 26. Radio tower M2 is located 200 miles due west...Ch. 10 - Prob. 27RECh. 10 - Prob. 28RECh. 10 - Prob. 29RECh. 10 - Prob. 30RECh. 10 - In Exercises 27-33, find the vertex, focus, and...Ch. 10 - Prob. 32RECh. 10 - Prob. 33RECh. 10 - Prob. 34RECh. 10 - Prob. 35RECh. 10 - Prob. 36RECh. 10 - Prob. 37RECh. 10 - Prob. 38RECh. 10 - In Exercises 39 42, identify the conic represented...Ch. 10 - In Exercises 39-42, identify the conic represented...Ch. 10 - In Exercises 39-42, identify the conic represented...Ch. 10 - In Exercises 39-42. identify the conic represented...Ch. 10 - In Exercises 43 -46, identify the conic...Ch. 10 - In Exercises 43 -46, identify the conic...Ch. 10 - In Exercises 43 -46, identify the conic...Ch. 10 - In Exercises 43 -46 , identify the conic...Ch. 10 - Prob. 47RECh. 10 - Prob. 48RECh. 10 - Prob. 49RECh. 10 - Prob. 50RECh. 10 - Prob. 51RECh. 10 - In Exercises 52 -57. eliminate the parameter and...Ch. 10 - In Exercises 52 -57 . eliminate the parameter and...Ch. 10 - In Exercises 52 -57, eliminate the parameter and...Ch. 10 - In Exercises 52 -57. eliminate the parameter and...Ch. 10 - In Exercises 52 -57. eliminate the parameter and...Ch. 10 - In Exercises 52 -57. eliminate the parameter and...Ch. 10 - Find two different sets of parametric equations...Ch. 10 - 59. The path of a projectile that is launched h...Ch. 10 - Prob. 60RECh. 10 - Prob. 61RECh. 10 - Prob. 62RECh. 10 - Prob. 63RECh. 10 - Prob. 64RECh. 10 - Prob. 65RECh. 10 - In Exercises 1-5. graph the conic section with the...Ch. 10 - Prob. 2TCh. 10 - Prob. 3TCh. 10 - Prob. 4TCh. 10 - Prob. 5TCh. 10 - In Exercises 6-8, find the standard form of the...Ch. 10 - Prob. 7TCh. 10 - In Exercises 6-8, find the standard form of the...Ch. 10 - In Exercises 6 ft, find the standard form of the...Ch. 10 - 10. An engineer is designing headlight units for...Ch. 10 - In Exercises 11-12, identify each equation without...Ch. 10 - In Exercises 11-12, identify each equation without...Ch. 10 - Prob. 13TCh. 10 - In Exercises 14 -15. eliminate the parameter and...Ch. 10 - In Exercises 14-15 eliminate the parameter and...Ch. 10 - Prob. 16TCh. 10 - Prob. 17TCh. 10 - Solve each equation or inequality in Exercises...Ch. 10 - Solve each equation or inequality in Exercises...Ch. 10 - Solve each equation or inequality in Exercises...Ch. 10 - Solve each equation or inequality in Exercises...Ch. 10 - Solve each equation or inequality in Exercises...Ch. 10 - Solve each equation or inequality in Exercises...Ch. 10 - Solve each equation or inequality in Exercises...Ch. 10 - Solve each system in Exercises 8-10. 8.
Ch. 10 - Solve each system in Exercises 8-10. 9. {...Ch. 10 - Solve each system in Exercises 8-10. (Use...Ch. 10 - In Exercises 11-13, graph each equation, function,...Ch. 10 - In Exercises 11-13, graph each equation, function,...Ch. 10 - In Exercises 11-13, graph each equation, function,...Ch. 10 - a. List all possible rational roots of...Ch. 10 - 15. The figure shows ihe graph of and its two...Ch. 10 - 16. If
Ch. 10 - 17. Expand using logarithmic properties. Where...Ch. 10 - 18. Write the slope-intercept form of the equation...Ch. 10 - Rent-a-Truck charges a daily rental rate for a...Ch. 10 - The local cable television company offers two...Ch. 10 - 21. Verify the identity:
Ch. 10 - Graph one complete cycle of y=2cos(2x+).Ch. 10 - Prob. 23CRECh. 10 - Solve for :sin2=sin,02.Ch. 10 - In oblique triangle ABC,A=64,B=72,anda=13.6. Solve...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Similar questions
- Solve the problems on the imagearrow_forwardAsked this question and got a wrong answer previously: Third, show that v3 = (−√3, −3, 3)⊤ is an eigenvector of M3 . Also here find the correspondingeigenvalue λ3 . Just from looking at M3 and its components, can you say something about the remaining twoeigenvalues? If so, what would you say?arrow_forwardDetermine whether the inverse of f(x)=x^4+2 is a function. Then, find the inverse.arrow_forward
- The 173 acellus.com StudentFunctions inter ooks 24-25/08 R Mastery Connect ac ?ClassiD-952638111# Introduction - Surface Area of Composite Figures 3 cm 3 cm 8 cm 8 cm Find the surface area of the composite figure. 2 SA = [?] cm² 7 cm REMEMBER! Exclude areas where complex shapes touch. 7 cm 12 cm 10 cm might ©2003-2025 International Academy of Science. All Rights Reserved. Enterarrow_forwardYou are given a plane Π in R3 defined by two vectors, p1 and p2, and a subspace W in R3 spanned by twovectors, w1 and w2. Your task is to project the plane Π onto the subspace W.First, answer the question of what the projection matrix is that projects onto the subspace W and how toapply it to find the desired projection. Second, approach the task in a different way by using the Gram-Schmidtmethod to find an orthonormal basis for subspace W, before then using the resulting basis vectors for theprojection. Last, compare the results obtained from both methodsarrow_forwardPlane II is spanned by the vectors: - (2) · P² - (4) P1=2 P21 3 Subspace W is spanned by the vectors: 2 W1 - (9) · 1 W2 1 = (³)arrow_forward
- show that v3 = (−√3, −3, 3)⊤ is an eigenvector of M3 . Also here find the correspondingeigenvalue λ3 . Just from looking at M3 and its components, can you say something about the remaining twoeigenvalues? If so, what would you say? find v42 so that v4 = ( 2/5, v42, 1)⊤ is an eigenvector of M4 with corresp. eigenvalue λ4 = 45arrow_forwardChapter 4 Quiz 2 As always, show your work. 1) FindΘgivencscΘ=1.045. 2) Find Θ given sec Θ = 4.213. 3) Find Θ given cot Θ = 0.579. Solve the following three right triangles. B 21.0 34.6° ca 52.5 4)c 26° 5) A b 6) B 84.0 a 42° barrow_forwardQ1: A: Let M and N be two subspace of finite dimension linear space X, show that if M = N then dim M = dim N but the converse need not to be true. B: Let A and B two balanced subsets of a linear space X, show that whether An B and AUB are balanced sets or nor. Q2: Answer only two A:Let M be a subset of a linear space X, show that M is a hyperplane of X iff there exists ƒ€ X'/{0} and a € F such that M = (x = x/f&x) = x}. fe B:Show that every two norms on finite dimension linear space are equivalent C: Let f be a linear function from a normed space X in to a normed space Y, show that continuous at x, E X iff for any sequence (x) in X converge to Xo then the sequence (f(x)) converge to (f(x)) in Y. Q3: A:Let M be a closed subspace of a normed space X, constract a linear space X/M as normed space B: Let A be a finite dimension subspace of a Banach space X, show that A is closed. C: Show that every finite dimension normed space is Banach space.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Evaluating Indefinite Integrals; Author: Professor Dave Explains;https://www.youtube.com/watch?v=-xHA2RjVkwY;License: Standard YouTube License, CC-BY
Calculus - Lesson 16 | Indefinite and Definite Integrals | Don't Memorise; Author: Don't Memorise;https://www.youtube.com/watch?v=bMnMzNKL9Ks;License: Standard YouTube License, CC-BY