To graph: The solutions of d y d t = − 1 2 y ln ( y 30 ) with the initial conditions y ( 0 ) = 1 y ( 0 ) = 20 , y ( 0 ) = 40 using the graph with the relative maximum at y ≈ 11.0364 and y -intercept at y = 30 , where the graph of d y d t = − 1 2 y ln ( y 30 ) is given below:

Question

Want to see the full answer?

Answer 1

Question

System that uses coordinates to uniquely determine the position of points. The most common coordinate system is the Cartesian system, where points are given by distance along a horizontal x-axis and vertical y-axis from the origin. A polar coordinate system locates a point by its direction relative to a reference direction and its distance from a given point. In three dimensions, it leads to cylindrical and spherical coordinates.

Chapter 10.5, Problem 16E

To determine

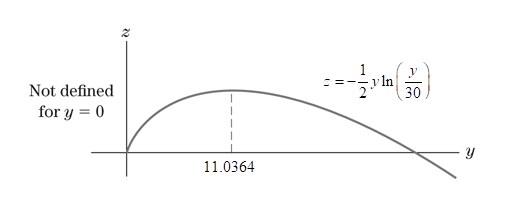
To graph: The solutions of dydt = −12yln(y30) with the initial conditions y(0) = 1 y(0) = 20,y(0)=40 using the graph with the relative maximum at y≈11.0364 and

y-intercept at y=30, where the graph of dydt = −12yln(y30) is given below:

Expert Solution & Answer

Want to see the full answer?

Check out a sample textbook solution

See solution

Students have asked these similar questions

3. Consider the sequences of functions f₁: [-π, π] → R, sin(n²x) An(2) n f pointwise as (i) Find a function ƒ : [-T,π] → R such that fn n∞. Further, show that fn →f uniformly on [-π,π] as n → ∞. [20 Marks] (ii) Does the sequence of derivatives f(x) has a pointwise limit on [-7, 7]? Justify your answer. [10 Marks]

1. (i) Give the definition of a metric on a set X. [5 Marks] (ii) Let X = {a, b, c} and let a function d : XxX → [0, ∞) be defined as d(a, a) = d(b,b) = d(c, c) 0, d(a, c) = d(c, a) 1, d(a, b) = d(b, a) = 4, d(b, c) = d(c,b) = 2. Decide whether d is a metric on X. Justify your answer. = (iii) Consider a metric space (R, d.), where = [10 Marks] 0 if x = y, d* (x, y) 5 if xy. In the metric space (R, d*), describe: (a) open ball B2(0) of radius 2 centred at 0; (b) closed ball B5(0) of radius 5 centred at 0; (c) sphere S10 (0) of radius 10 centred at 0. [5 Marks] [5 Marks] [5 Marks]

(c) sphere S10 (0) of radius 10 centred at 0. [5 Marks] 2. Let C([a, b]) be the metric space of continuous functions on the interval [a, b] with the metric doo (f,g) = max f(x)g(x)|. xЄ[a,b] = 1x. Find: Let f(x) = 1 - x² and g(x): (i) do(f, g) in C'([0, 1]); (ii) do(f,g) in C([−1, 1]). [20 Marks] [20 Marks]

Answer 2

Question

System that uses coordinates to uniquely determine the position of points. The most common coordinate system is the Cartesian system, where points are given by distance along a horizontal x-axis and vertical y-axis from the origin. A polar coordinate system locates a point by its direction relative to a reference direction and its distance from a given point. In three dimensions, it leads to cylindrical and spherical coordinates.

Chapter 10.5, Problem 16E

To determine

To graph: The solutions of dydt = −12yln(y30) with the initial conditions y(0) = 1 y(0) = 20,y(0)=40 using the graph with the relative maximum at y≈11.0364 and

y-intercept at y=30, where the graph of dydt = −12yln(y30) is given below:

Expert Solution & Answer

Want to see the full answer?

Check out a sample textbook solution

See solution

Answer 3

Question

System that uses coordinates to uniquely determine the position of points. The most common coordinate system is the Cartesian system, where points are given by distance along a horizontal x-axis and vertical y-axis from the origin. A polar coordinate system locates a point by its direction relative to a reference direction and its distance from a given point. In three dimensions, it leads to cylindrical and spherical coordinates.

Chapter 10.5, Problem 16E

To determine

To graph: The solutions of dydt = −12yln(y30) with the initial conditions y(0) = 1 y(0) = 20,y(0)=40 using the graph with the relative maximum at y≈11.0364 and

y-intercept at y=30, where the graph of dydt = −12yln(y30) is given below:

Expert Solution & Answer

Want to see the full answer?

Check out a sample textbook solution

See solution

Answer 4

Question

System that uses coordinates to uniquely determine the position of points. The most common coordinate system is the Cartesian system, where points are given by distance along a horizontal x-axis and vertical y-axis from the origin. A polar coordinate system locates a point by its direction relative to a reference direction and its distance from a given point. In three dimensions, it leads to cylindrical and spherical coordinates.

Chapter 10.5, Problem 16E

To determine

To graph: The solutions of dydt = −12yln(y30) with the initial conditions y(0) = 1 y(0) = 20,y(0)=40 using the graph with the relative maximum at y≈11.0364 and

y-intercept at y=30, where the graph of dydt = −12yln(y30) is given below:

Expert Solution & Answer

Want to see the full answer?

Check out a sample textbook solution

See solution

Answer 5

Chapter 10.5, Problem 16E

To determine

To graph: The solutions of dydt = −12yln(y30) with the initial conditions y(0) = 1 y(0) = 20,y(0)=40 using the graph with the relative maximum at y≈11.0364 and

y-intercept at y=30, where the graph of dydt = −12yln(y30) is given below:

Answer 6

Chapter 10.5, Problem 16E

To determine

To graph: The solutions of dydt = −12yln(y30) with the initial conditions y(0) = 1 y(0) = 20,y(0)=40 using the graph with the relative maximum at y≈11.0364 and

y-intercept at y=30, where the graph of dydt = −12yln(y30) is given below:

Answer 7

Chapter 10.5, Problem 16E

To determine

To graph: The solutions of dydt = −12yln(y30) with the initial conditions y(0) = 1 y(0) = 20,y(0)=40 using the graph with the relative maximum at y≈11.0364 and

y-intercept at y=30, where the graph of dydt = −12yln(y30) is given below:

Answer 8

Expert Solution & Answer

Answer 9

Expert Solution & Answer

Answer 10

Want to see the full answer?

Check out a sample textbook solution

See solution

Answer 11

Ch. 10.1 - Show that any function of the form y=Aet3/3, where...Ch. 10.1 - If the function f(t) is a solution of the...Ch. 10.1 - Prob. 3CYU Ch. 10.1 - Show that the function f(t)=32et212 is a solution...Ch. 10.1 - Show that the function f(t)=t212 is a solution of...Ch. 10.1 - Show that the function f(t)=5e2t satisfies...Ch. 10.1 - Show that the function f(t)=(et+1)1 satisfies...Ch. 10.1 - Prob. 5E Ch. 10.1 - Prob. 6E Ch. 10.1 - Is the constant function f(t)=3 a solution of the...

To graph: The solutions of d y d t = − 1 2 y ln ( y 30 ) with the initial conditions y ( 0 ) = 1 y ( 0 ) = 20 , y ( 0 ) = 40 using the graph with the relative maximum at y ≈ 11.0364 and y -intercept at y = 30 , where the graph of d y d t = − 1 2 y ln ( y 30 ) is given below:

Solution Summary: The author explains the graph of dyt= -fruc12y

Concept explainers

Videos

To graph: The solutions of dydt = −12yln(y30) with the initial conditions y(0) = 1 y(0) = 20,y(0)=40 using the graph with the relative maximum at y≈11.0364 and

y-intercept at y=30, where the graph of dydt = −12yln(y30) is given below:

Want to see the full answer?

Chapter 10 Solutions

To graph: The solutions of d y d t = − 1 2 y ln ( y 30 ) with the initial conditions y ( 0 ) = 1 y ( 0 ) = 20 , y ( 0 ) = 40 using the graph with the relative maximum at y ≈ 11.0364 and y -intercept at y = 30 , where the graph of d y d t = − 1 2 y ln ( y 30 ) is given below:

Solution Summary: The author explains the graph of dyt= -fruc12y

Concept explainers

Videos

To graph: The solutions of dydt = −12yln(y30) with the initial conditions y(0) = 1 y(0) = 20,y(0)=40 using the graph with the relative maximum at y≈11.0364 and y-intercept at y=30, where the graph of dydt = −12yln(y30) is given below:

Want to see the full answer?

Chapter 10 Solutions

To graph: The solutions of dydt = −12yln(y30) with the initial conditions y(0) = 1 y(0) = 20,y(0)=40 using the graph with the relative maximum at y≈11.0364 and

y-intercept at y=30, where the graph of dydt = −12yln(y30) is given below: