Calculus: Early Transcendentals
8th Edition
ISBN: 9781285741550
Author: James Stewart
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 10.4, Problem 44E
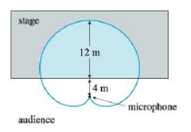
When recording live performances, sound engineers often use a microphone with a cardioid pickup pattern because it suppresses noise from the audience. Suppose the microphone is placed 4 m from the front of the stage (as in the figure) and the boundary of the optimal pickup region is given by the cardioid r = 8 + 8 sin θ, where r is measured in meters and the microphone is at the pole. The musicians want to know the area they will have on stage within the optimal pickup range of the microphone. Answer their question.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
See image for question
For this question, refer to the a1q4.py Python code that follows the assignment, as well as the dataprovided after the assignment.(a) Modify the code presented to plot the data from the two separate sets of information(from each region).(b) For each population of squirbos, let ` be the length of their front claws and s the mass ofthe skull. Determine for what value of m the s is isometric to `m. Justify it with your log − log plotsfrom (a) and suitable sketched lines.(c) What do you notice about the correlus striatus on your plot?(d) What historically might explain their situation?
Please see image for question.
Chapter 10 Solutions
Calculus: Early Transcendentals
Ch. 10.1 - Sketch the curve by using the parametric equations...Ch. 10.1 - Sketch the curve by using the parametric equations...Ch. 10.1 - Prob. 3ECh. 10.1 - Prob. 4ECh. 10.1 - Prob. 5ECh. 10.1 - Prob. 6ECh. 10.1 - Prob. 7ECh. 10.1 - Prob. 8ECh. 10.1 - Prob. 9ECh. 10.1 - Prob. 10E
Ch. 10.1 - (a) Eliminate the parameter to find a Cartesian...Ch. 10.1 - (a) Eliminate the parameter to find a Cartesian...Ch. 10.1 - (a) Eliminate the parameter to find a Cartesian...Ch. 10.1 - Prob. 14ECh. 10.1 - (a) Eliminate the parameter to find a Cartesian...Ch. 10.1 - Prob. 16ECh. 10.1 - Prob. 17ECh. 10.1 - (a) Eliminate the parameter to find a Cartesian...Ch. 10.1 - Describe the motion of a particle with position...Ch. 10.1 - Describe the motion of a particle with position...Ch. 10.1 - Describe the motion of a particle with position...Ch. 10.1 - Describe the motion of a particle with position...Ch. 10.1 - Suppose a curve is given by the parametric...Ch. 10.1 - Match the graphs of the parametric equations x =...Ch. 10.1 - Prob. 25ECh. 10.1 - Prob. 26ECh. 10.1 - Prob. 27ECh. 10.1 - Match the parametric equations with the graphs...Ch. 10.1 - Graph the curve x = y 2 sin y.Ch. 10.1 - Graph the curves y = x3 4x and x = y3 4y and...Ch. 10.1 - (a) Show that the parametric equations x = x1 +...Ch. 10.1 - Use a graphing device and the result of Exercise...Ch. 10.1 - Find parametric equations for the path of a...Ch. 10.1 - (a) Find parametric equations for the ellipse...Ch. 10.1 - Use a graphing calculator or computer to reproduce...Ch. 10.1 - Use a graphing calculator or computer to reproduce...Ch. 10.1 - Compare the curves represented by the parametric...Ch. 10.1 - Prob. 38ECh. 10.1 - Derive Equations 1 for the case /2Ch. 10.1 - Let P be a point at a distance d from the center...Ch. 10.1 - If a and b are fixed numbers, find parametric...Ch. 10.1 - If a and b are fixed numbers, find parametric...Ch. 10.1 - A curve, called a witch of Maria Agnesi, consists...Ch. 10.1 - (a) Find parametric equations for the set of all...Ch. 10.1 - Suppose that the position of one particle at time...Ch. 10.1 - If a projectile is fired with an initial velocity...Ch. 10.1 - Investigate the family of curves defined by the...Ch. 10.1 - The swallowtail catastrophe curves are defined by...Ch. 10.1 - Graph several members of the family of curves with...Ch. 10.1 - Graph several members of the family of curves x =...Ch. 10.1 - Prob. 51ECh. 10.1 - Prob. 52ECh. 10.2 - Find dy/dx. 1. x=t1+t,y=1+tCh. 10.2 - Find dy/dx. 2. x = tet, y = t + sin tCh. 10.2 - Find an equation of the tangent to the curve at...Ch. 10.2 - Find an equation of the tangent to the curve at...Ch. 10.2 - Find an equation of the tangent to the curve at...Ch. 10.2 - Find an equation of the tangent to the curve at...Ch. 10.2 - Find an equation of the tangent to the curve at...Ch. 10.2 - Find an equation of the tangent to the curve at...Ch. 10.2 - Find an equation of the tangent to the curve at...Ch. 10.2 - Find an equation of the tangent to the curve at...Ch. 10.2 - Find dy/dx and d2y/dx2. For which values of t is...Ch. 10.2 - Find dy/dx and d2y/dx2. For which values of t is...Ch. 10.2 - Find dy/dx and d2y/dx2. For which values of t is...Ch. 10.2 - Find dy/dx and d2y/dx2. For which values of t is...Ch. 10.2 - Find dy/dx and d2y/dx2. For which values of t is...Ch. 10.2 - Find dy/dx and d2y/dx2. For which values of t is...Ch. 10.2 - Find the points on the curve where the tangent is...Ch. 10.2 - Find the points on the curve where the tangent is...Ch. 10.2 - Find the points on the curve where the tangent is...Ch. 10.2 - Find the points on the curve where the tangent is...Ch. 10.2 - Use a graph to estimate the coordinates of the...Ch. 10.2 - Prob. 22ECh. 10.2 - Graph the curve in a viewing rectangle that...Ch. 10.2 - Graph the curve in a viewing rectangle that...Ch. 10.2 - Show that the curve x = cos t, y = sin t cos t has...Ch. 10.2 - Prob. 26ECh. 10.2 - (a) Find the slope of the tangent line to the...Ch. 10.2 - (a) Find the slope of the tangent to the astroid x...Ch. 10.2 - At what point(s) on the curve x = 3t2 + 1, y = t3 ...Ch. 10.2 - Find equations of the tangents to the curve x =...Ch. 10.2 - Use the parametric equations of an ellipse, x = a...Ch. 10.2 - Find the area enclosed by the curve x = t2 2t,...Ch. 10.2 - Find the area enclosed by the x-axis and the curve...Ch. 10.2 - Find the area of the region enclosed by the...Ch. 10.2 - Find the area under one arch of the trochoid of...Ch. 10.2 - Let be the region enclosed by the loop of the...Ch. 10.2 - Set up an integral that represents the length of...Ch. 10.2 - Set up an integral that represents the length of...Ch. 10.2 - Set up an integral that represents the length of...Ch. 10.2 - Prob. 40ECh. 10.2 - Find the exact length of the curve. 41. x = 1 +...Ch. 10.2 - Find the exact length of the curve. 42. x = et t,...Ch. 10.2 - Find the exact length of the curve. 43. x = t sin...Ch. 10.2 - Find the exact length of the curve. 44. x = 3 cos...Ch. 10.2 - Graph the curve and find its exact length. 45. x =...Ch. 10.2 - Graph the curve and find its exact length. 46....Ch. 10.2 - Graph the curve x = sin t + sin 1.5t, y = cos t...Ch. 10.2 - Find the length of the loop of the curve x = 3t ...Ch. 10.2 - Prob. 49ECh. 10.2 - In Exercise 10.1.43 you were asked to derive the...Ch. 10.2 - Find the distance traveled by a particle with...Ch. 10.2 - Find the distance traveled by a particle with...Ch. 10.2 - Show that the total length of the ellipse x = a...Ch. 10.2 - Prob. 54ECh. 10.2 - (a) Graph the epitrochoid with equations x = 11...Ch. 10.2 - Set up an integral that represents the area of the...Ch. 10.2 - Prob. 58ECh. 10.2 - Prob. 59ECh. 10.2 - Prob. 60ECh. 10.2 - Find the exact area of the surface obtained by...Ch. 10.2 - Find the exact area of the surface obtained by...Ch. 10.2 - Find the exact area of the surface obtained by...Ch. 10.2 - Prob. 64ECh. 10.2 - Find the surface area generated by rotating the...Ch. 10.2 - Prob. 66ECh. 10.2 - Prob. 67ECh. 10.2 - Prob. 68ECh. 10.2 - Prob. 69ECh. 10.2 - Prob. 70ECh. 10.2 - Prob. 71ECh. 10.2 - Prob. 72ECh. 10.2 - Prob. 73ECh. 10.2 - A cow is tied to a silo with radius r by a rope...Ch. 10.3 - Plot the point whose polar coordinates are given....Ch. 10.3 - Prob. 2ECh. 10.3 - Plot the point whose polar coordinates are given....Ch. 10.3 - Plot the point whose polar coordinates are given....Ch. 10.3 - Prob. 5ECh. 10.3 - Prob. 6ECh. 10.3 - Sketch the region in the plane consisting of...Ch. 10.3 - Prob. 8ECh. 10.3 - Sketch the region in the plane consisting of...Ch. 10.3 - Prob. 10ECh. 10.3 - Sketch the region in the plane consisting of...Ch. 10.3 - Prob. 12ECh. 10.3 - Find the distance between the points with polar...Ch. 10.3 - Prob. 14ECh. 10.3 - Identify the curve by finding a Cartesian equation...Ch. 10.3 - Prob. 16ECh. 10.3 - Identify the curve by finding a Cartesian equation...Ch. 10.3 - Identify the curve by finding a Cartesian equation...Ch. 10.3 - Identify the curve by finding a Cartesian equation...Ch. 10.3 - Prob. 20ECh. 10.3 - Find a polar equation for the curve represented by...Ch. 10.3 - Find a polar equation for the curve represented by...Ch. 10.3 - Prob. 23ECh. 10.3 - Prob. 24ECh. 10.3 - Prob. 25ECh. 10.3 - Find a polar equation for the curve represented by...Ch. 10.3 - Prob. 27ECh. 10.3 - Prob. 28ECh. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Prob. 32ECh. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Prob. 34ECh. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Prob. 44ECh. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Prob. 46ECh. 10.3 - Prob. 47ECh. 10.3 - Prob. 48ECh. 10.3 - Prob. 49ECh. 10.3 - Show that the curve r = 2 csc (also a conchoid)...Ch. 10.3 - Show that the curve r = sin tan (called a...Ch. 10.3 - Sketch the curve (x2 + y2)3 = 4x2y2.Ch. 10.3 - (a) In Example 11 the graphs suggest that the...Ch. 10.3 - Prob. 54ECh. 10.3 - Find the slope of the tangent line to the given...Ch. 10.3 - Find the slope of the tangent line to the given...Ch. 10.3 - Find the slope of the tangent line to the given...Ch. 10.3 - Find the slope of the tangent line to the given...Ch. 10.3 - Find the slope of the tangent line to the given...Ch. 10.3 - Find the slope of the tangent line to the given...Ch. 10.3 - Find the points on the given curve where the...Ch. 10.3 - Find the points on the given curve where the...Ch. 10.3 - Find the points on the given curve where the...Ch. 10.3 - Prob. 64ECh. 10.3 - Prob. 65ECh. 10.3 - Show that the curves r = a sin and r = a cos ...Ch. 10.3 - Use a graphing device to graph the polar curve....Ch. 10.3 - Use a graphing device to graph the polar curve....Ch. 10.3 - Use a graphing device to graph the polar curve....Ch. 10.3 - Prob. 70ECh. 10.3 - Prob. 71ECh. 10.3 - Prob. 72ECh. 10.3 - Prob. 73ECh. 10.3 - Prob. 74ECh. 10.3 - Prob. 75ECh. 10.3 - Prob. 76ECh. 10.3 - Let P be any point (except the origin) on the...Ch. 10.3 - Prob. 78ECh. 10.4 - Find the area of the region that is bounded by the...Ch. 10.4 - Find the area of the region that is bounded by the...Ch. 10.4 - Find the area of the region that is bounded by the...Ch. 10.4 - Find the area of the region that is bounded by the...Ch. 10.4 - Find the area of the shaded region. 5.Ch. 10.4 - Find the area of the shaded region. 6.Ch. 10.4 - Find the area of the shaded region. 7.Ch. 10.4 - Find the area of the shaded region. 8.Ch. 10.4 - Sketch the curve and find the area that it...Ch. 10.4 - Sketch the curve and find the area that it...Ch. 10.4 - Sketch the curve and find the area that it...Ch. 10.4 - Sketch the curve and find the area that it...Ch. 10.4 - Graph the curve and find the area that it...Ch. 10.4 - Prob. 14ECh. 10.4 - Prob. 15ECh. 10.4 - Prob. 16ECh. 10.4 - Find the area of the region enclosed by one loop...Ch. 10.4 - Find the area of the region enclosed by one loop...Ch. 10.4 - Find the area of the region enclosed by one loop...Ch. 10.4 - Find the area of the region enclosed by one loop...Ch. 10.4 - Find the area of the region enclosed by one loop...Ch. 10.4 - Find the area enclosed by the loop of the...Ch. 10.4 - Find the area of the region that lies inside the...Ch. 10.4 - Find the area of the region that lies inside the...Ch. 10.4 - Find the area of the region that lies inside the...Ch. 10.4 - Find the area of the region that lies inside the...Ch. 10.4 - Find the area of the region that lies inside the...Ch. 10.4 - Find the area of the region that lies inside the...Ch. 10.4 - Find the area of the region that lies inside both...Ch. 10.4 - Find the area of the region that lies inside both...Ch. 10.4 - Find the area of the region that lies inside both...Ch. 10.4 - Find the area of the region that lies inside both...Ch. 10.4 - Find the area of the region that lies inside both...Ch. 10.4 - Prob. 34ECh. 10.4 - Find the area inside the larger loop and outside...Ch. 10.4 - Find the area between a large loop and the...Ch. 10.4 - Find all points of intersection of the given...Ch. 10.4 - Find all points of intersection of the given...Ch. 10.4 - Find all points of intersection of the given...Ch. 10.4 - Prob. 40ECh. 10.4 - Find all points of intersection of the given...Ch. 10.4 - Prob. 42ECh. 10.4 - The points of intersection of the cardioid r = 1 +...Ch. 10.4 - When recording live performances, sound engineers...Ch. 10.4 - Find the exact length of the polar curve. 45. r =...Ch. 10.4 - Find the exact length of the polar curve. 46. r =...Ch. 10.4 - Find the exact length of the polar curve. 47. r =...Ch. 10.4 - Find the exact length of the polar curve. 48. r =...Ch. 10.4 - Find the exact length of the curve. Use a graph to...Ch. 10.4 - Find the exact length of the curve. Use a graph to...Ch. 10.4 - Use a calculator to find the length of the curve...Ch. 10.4 - Prob. 52ECh. 10.4 - Prob. 53ECh. 10.4 - Prob. 54ECh. 10.4 - (a) Use Formula 10.2.6 to show that the area of...Ch. 10.4 - Prob. 56ECh. 10.5 - Find the vertex, focus, and directrix of the...Ch. 10.5 - Find the vertex, focus, and directrix of the...Ch. 10.5 - Find the vertex, focus, and directrix of the...Ch. 10.5 - Prob. 4ECh. 10.5 - Find the vertex, focus, and directrix of the...Ch. 10.5 - Prob. 6ECh. 10.5 - Find the vertex, focus, and directrix of the...Ch. 10.5 - Find the vertex, focus, and directrix of the...Ch. 10.5 - Find an equation of the parabola. Then find the...Ch. 10.5 - Find an equation of the parabola. Then find the...Ch. 10.5 - Find the vertices and foci of the ellipse and...Ch. 10.5 - Prob. 12ECh. 10.5 - Find the vertices and foci of the ellipse and...Ch. 10.5 - Prob. 14ECh. 10.5 - Find the vertices and foci of the ellipse and...Ch. 10.5 - Find the vertices and foci of the ellipse and...Ch. 10.5 - Prob. 17ECh. 10.5 - Prob. 18ECh. 10.5 - Prob. 19ECh. 10.5 - Prob. 20ECh. 10.5 - Prob. 21ECh. 10.5 - Prob. 22ECh. 10.5 - Prob. 23ECh. 10.5 - Prob. 24ECh. 10.5 - Identify the type of conic section whose equation...Ch. 10.5 - Identify the type of conic section whose equation...Ch. 10.5 - Prob. 27ECh. 10.5 - Prob. 28ECh. 10.5 - Prob. 29ECh. 10.5 - Identify the type of conic section whose equation...Ch. 10.5 - Prob. 31ECh. 10.5 - Find an equation for the conic that satisfies the...Ch. 10.5 - Prob. 33ECh. 10.5 - Prob. 34ECh. 10.5 - Prob. 35ECh. 10.5 - Prob. 36ECh. 10.5 - Prob. 37ECh. 10.5 - Find an equation for the conic that satisfies the...Ch. 10.5 - Prob. 39ECh. 10.5 - Prob. 40ECh. 10.5 - Prob. 41ECh. 10.5 - Prob. 42ECh. 10.5 - Prob. 43ECh. 10.5 - Prob. 44ECh. 10.5 - Prob. 45ECh. 10.5 - Prob. 46ECh. 10.5 - Prob. 47ECh. 10.5 - Prob. 48ECh. 10.5 - The point in a lunar orbit nearest the surface of...Ch. 10.5 - A cross-section of a parabolic reflector is shown...Ch. 10.5 - The LORAN (LOng RAnge Navigation) radio navigation...Ch. 10.5 - Use the definition of a hyperbola to derive...Ch. 10.5 - Show that the function defined by the upper branch...Ch. 10.5 - Find an equation for the ellipse with foci (1, 1)...Ch. 10.5 - Determine the type of curve represented by the...Ch. 10.5 - Prob. 56ECh. 10.5 - Prob. 57ECh. 10.5 - Prob. 58ECh. 10.5 - Prob. 59ECh. 10.5 - Prob. 60ECh. 10.5 - Find the area of the region enclosed by the...Ch. 10.5 - Prob. 62ECh. 10.5 - Find the centroid of the region enclosed by the...Ch. 10.5 - Prob. 64ECh. 10.5 - Prob. 65ECh. 10.5 - Let P(x1, y1) be a point on the hyperbola x2/a2 ...Ch. 10.6 - Prob. 1ECh. 10.6 - Prob. 2ECh. 10.6 - Prob. 3ECh. 10.6 - Prob. 4ECh. 10.6 - Prob. 5ECh. 10.6 - Prob. 6ECh. 10.6 - Prob. 7ECh. 10.6 - Prob. 8ECh. 10.6 - Prob. 9ECh. 10.6 - Prob. 10ECh. 10.6 - Prob. 11ECh. 10.6 - Prob. 12ECh. 10.6 - Prob. 13ECh. 10.6 - Prob. 14ECh. 10.6 - Prob. 15ECh. 10.6 - Prob. 16ECh. 10.6 - Prob. 17ECh. 10.6 - Prob. 18ECh. 10.6 - Prob. 19ECh. 10.6 - Prob. 20ECh. 10.6 - Prob. 21ECh. 10.6 - Prob. 22ECh. 10.6 - Prob. 23ECh. 10.6 - Prob. 24ECh. 10.6 - Prob. 25ECh. 10.6 - Jupiter's orbit has eccentricity 0.048 and the...Ch. 10.6 - The orbit of Halleys comet, last seen in 1986 and...Ch. 10.6 - Prob. 28ECh. 10.6 - Prob. 29ECh. 10.6 - Prob. 30ECh. 10.6 - Prob. 31ECh. 10 - (a) What is a parametric curve? (b) How do you...Ch. 10 - Prob. 2RCCCh. 10 - Prob. 3RCCCh. 10 - Prob. 4RCCCh. 10 - Prob. 5RCCCh. 10 - Prob. 6RCCCh. 10 - Prob. 7RCCCh. 10 - Prob. 8RCCCh. 10 - (a) What is the eccentricity of a conic section?...Ch. 10 - Determine whether the statement is true or false....Ch. 10 - Determine whether the statement is true or false....Ch. 10 - Determine whether the statement is true or false....Ch. 10 - Determine whether the statement is true or false....Ch. 10 - Prob. 5RQCh. 10 - Determine whether the statement is true or false....Ch. 10 - Determine whether the statement is true or false....Ch. 10 - Determine whether the statement is true or false....Ch. 10 - Determine whether the statement is true or false....Ch. 10 - Determine whether the statement is true or false....Ch. 10 - Prob. 1RECh. 10 - Prob. 2RECh. 10 - Prob. 3RECh. 10 - Prob. 4RECh. 10 - Prob. 5RECh. 10 - Prob. 6RECh. 10 - Prob. 7RECh. 10 - Prob. 8RECh. 10 - Prob. 9RECh. 10 - Prob. 10RECh. 10 - Prob. 11RECh. 10 - Sketch the polar curve. 12. r = 3 + cos 3Ch. 10 - Prob. 13RECh. 10 - Prob. 14RECh. 10 - Prob. 15RECh. 10 - Prob. 16RECh. 10 - Prob. 17RECh. 10 - Prob. 18RECh. 10 - The curve with polar equation r = (sin )/ is...Ch. 10 - Prob. 20RECh. 10 - Prob. 21RECh. 10 - Prob. 22RECh. 10 - Prob. 23RECh. 10 - Prob. 24RECh. 10 - Prob. 25RECh. 10 - Prob. 26RECh. 10 - Prob. 27RECh. 10 - Prob. 28RECh. 10 - Prob. 29RECh. 10 - Prob. 30RECh. 10 - Find the area enclosed by the curve r2 = 9 cos 5.Ch. 10 - Prob. 32RECh. 10 - Prob. 33RECh. 10 - Prob. 34RECh. 10 - Find the area of the region that lies inside both...Ch. 10 - Find the area of the region that lies inside the...Ch. 10 - Prob. 37RECh. 10 - Prob. 38RECh. 10 - Prob. 39RECh. 10 - Prob. 40RECh. 10 - Prob. 41RECh. 10 - Prob. 42RECh. 10 - Prob. 43RECh. 10 - Prob. 44RECh. 10 - Prob. 45RECh. 10 - Prob. 46RECh. 10 - Prob. 47RECh. 10 - Prob. 48RECh. 10 - Prob. 49RECh. 10 - Prob. 50RECh. 10 - Prob. 51RECh. 10 - Prob. 52RECh. 10 - Prob. 53RECh. 10 - Prob. 54RECh. 10 - Prob. 55RECh. 10 - Prob. 56RECh. 10 - In the figure the circle of radius a is...Ch. 10 - A curve called the folium of Descartes is defined...Ch. 10 - The outer circle in the figure has radius 1 and...Ch. 10 - Prob. 2PCh. 10 - Prob. 3PCh. 10 - Four bugs are placed at the four corners of a...Ch. 10 - Prob. 5PCh. 10 - A circle C of radius 2r has its center at the...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Question 2 Find the shortest distance between the lines [x, y, z] = [1,0,4] + t[1, 3, −1] and [x, y, z] = [0,2,0] + s[2, 1, 1]. [Do not use derivatives.]arrow_forwardPlease see image for the questions.arrow_forwardUse the following graphs to evaluate the given one-sided limit. Answer exactly. y = f (x): y = g(x): 8 6 ν -8-6-4-2 2- 1-2-2 -4 -6 -8 ° 4 lim (f(x)+g(x)) = x+2+ 8 6 2 ν 0 x x 6 8 -8 -6-4-2 2 6 8 -2 -4 -6 -8arrow_forward
- Question 1 The points A = (-2, 3, 2) and B = (4, 1, 4) are reflections of one another in a plane S. Find an equation for S.arrow_forwardThe graph below is the function f (x) -D -3-2 4 3 2 Q2 03 Find lim f(x) = x-1- Find lim f(x) = x−1+ Find lim f(x) = x-1 Find f (-1) = 3 4 5arrow_forwardi circled the correct answer and i did most of the question but i cant figure out how to add both residues to get the correct answer could you please show me how to do itarrow_forward
- Question 3 Starting at the point (0, −2,0), I walk up the hill z = 4-x² — y². The projection of my path on the xy plane is the line y = 2x-2. (a) At what point on my path is my altitude (the z-value) the greatest? (b) What is the slope m of my path (taking the z-axis to be vertical) when I am at the point (1, 0, 3)? [Hint: Parametrize my path (take x to be t).]arrow_forwardI circled the correct, could you explain using stokearrow_forwardUse Euler's method to numerically integrate dy dx -2x+12x² - 20x +8.5 from x=0 to x=4 with a step size of 0.5. The initial condition at x=0 is y=1. Recall that the exact solution is given by y = -0.5x+4x³- 10x² + 8.5x+1arrow_forward
- Find an equation of the line tangent to the graph of f(x) = (5x-9)(x+4) at (2,6).arrow_forwardFind the point on the graph of the given function at which the slope of the tangent line is the given slope. 2 f(x)=8x²+4x-7; slope of the tangent line = -3arrow_forwardUse the product rule to find the derivative of the following. p(y) (y¹ + y²) (6y¯³-10y¯4)arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Functions and Change: A Modeling Approach to Coll...
Algebra
ISBN:9781337111348
Author:Bruce Crauder, Benny Evans, Alan Noell
Publisher:Cengage Learning
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Area Between The Curve Problem No 1 - Applications Of Definite Integration - Diploma Maths II; Author: Ekeeda;https://www.youtube.com/watch?v=q3ZU0GnGaxA;License: Standard YouTube License, CC-BY