Pre-Algebra, Student Edition
1st Edition
ISBN: 9780078885150
Author: McGraw-Hill
Publisher: Glencoe/McGraw-Hill
expand_more
expand_more
format_list_bulleted
Videos
Question
Chapter 10.4, Problem 42STP
i.
To determine
Write the process of calculating distance between home plate to second base from figure.
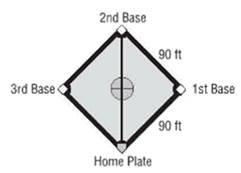
i.
Expert Solution
Answer to Problem 42STP
Distance between home plate to second base can be calculated using Pythagoras theorem.
Explanation of Solution
Given:
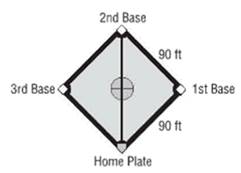
Calculations:
We have given baseball playground base. It is having square shape.
Here, we have to find distance from home base to second base.
According to figure, considering area from home base, first base and second base, it forms right angle
Therefore we can use Pythagoras theorem to calculate distance between home base to second base.
Here,
Distance between home base to first base = 90 ft
Distance between first base to second base = 90ft
As per Pythagoras theorem, hypotenuse square is equal to sum of square of remaining two sides.
Here, hypotenuse is distance from home base to second base.
Conclusion:
Therefore, we are able to calculate distance from home base to second base using Pythagoras theorem.
ii.
To determine
Calculate distance between home plate to second base from figure.
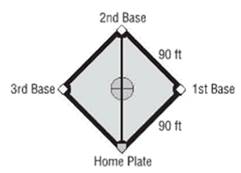
ii.
Expert Solution
Answer to Problem 42STP
Distance between home plate to second base from figure is 127.279ft
Explanation of Solution
Given:
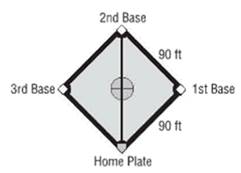
Calculation:
Here, we have to find value of hypotenuse that is distance from home plate to second plate.
Distance between home base to first base = 90 ft
Distance between first base to second base = 90ft
As per Pythagoras theorem,
Conclusion:
Therefore, we are able to calculate distance from home base to second base using Pythagoras theorem.
Chapter 10 Solutions
Pre-Algebra, Student Edition
Ch. 10.1 - Prob. 1ACYPCh. 10.1 - Prob. 1BCYPCh. 10.1 - Prob. 1CCYPCh. 10.1 - Prob. 1DCYPCh. 10.1 - Prob. 2ACYPCh. 10.1 - Prob. 2BCYPCh. 10.1 - Prob. 3ACYPCh. 10.1 - Prob. 3BCYPCh. 10.1 - Prob. 4ACYPCh. 10.1 - Prob. 4BCYP
Ch. 10.1 - Prob. 4CCYPCh. 10.1 - Prob. 4DCYPCh. 10.1 - Prob. 5CYPCh. 10.1 - Prob. 1CYUCh. 10.1 - Prob. 2CYUCh. 10.1 - Prob. 3CYUCh. 10.1 - Prob. 4CYUCh. 10.1 - Prob. 5CYUCh. 10.1 - Prob. 6CYUCh. 10.1 - Prob. 7CYUCh. 10.1 - Prob. 8CYUCh. 10.1 - Prob. 9CYUCh. 10.1 - Prob. 10CYUCh. 10.1 - Prob. 11PPSCh. 10.1 - Prob. 12PPSCh. 10.1 - Prob. 13PPSCh. 10.1 - Prob. 14PPSCh. 10.1 - Prob. 15PPSCh. 10.1 - Prob. 16PPSCh. 10.1 - Prob. 17PPSCh. 10.1 - Prob. 18PPSCh. 10.1 - Prob. 19PPSCh. 10.1 - Prob. 20PPSCh. 10.1 - Prob. 21PPSCh. 10.1 - Prob. 22PPSCh. 10.1 - Prob. 23PPSCh. 10.1 - Prob. 24PPSCh. 10.1 - Prob. 25PPSCh. 10.1 - Prob. 26PPSCh. 10.1 - Prob. 27PPSCh. 10.1 - Prob. 28PPSCh. 10.1 - Prob. 29PPSCh. 10.1 - Prob. 30PPSCh. 10.1 - Prob. 31PPSCh. 10.1 - Prob. 32PPSCh. 10.1 - Prob. 33PPSCh. 10.1 - Prob. 34PPSCh. 10.1 - Prob. 35PPSCh. 10.1 - Prob. 36PPSCh. 10.1 - Prob. 37PPSCh. 10.1 - Prob. 38PPSCh. 10.1 - Prob. 39PPSCh. 10.1 - Prob. 40HPCh. 10.1 - Prob. 41HPCh. 10.1 - Prob. 42HPCh. 10.1 - Prob. 43HPCh. 10.1 - Prob. 44STPCh. 10.1 - Prob. 45STPCh. 10.1 - Prob. 46STPCh. 10.1 - Prob. 47STPCh. 10.1 - Prob. 48SRCh. 10.1 - Prob. 49SRCh. 10.1 - Prob. 50SRCh. 10.1 - Prob. 51SRCh. 10.1 - Prob. 52SRCh. 10.1 - Prob. 53SRCh. 10.1 - Prob. 54SRCh. 10.1 - Prob. 55SCh. 10.1 - Prob. 56SCh. 10.1 - Prob. 57SCh. 10.1 - Prob. 58SCh. 10.1 - Prob. 59SCh. 10.1 - Prob. 60SCh. 10.1 - Prob. 61SCh. 10.1 - Prob. 62SCh. 10.2 - Prob. 1ACYPCh. 10.2 - Prob. 1BCYPCh. 10.2 - Prob. 1CCYPCh. 10.2 - Prob. 1DCYPCh. 10.2 - Prob. 2CYPCh. 10.2 - Prob. 3CYPCh. 10.2 - Prob. 4ACYPCh. 10.2 - Prob. 4BCYPCh. 10.2 - Prob. 5CYPCh. 10.2 - Prob. 1CYUCh. 10.2 - Prob. 2CYUCh. 10.2 - Prob. 3CYUCh. 10.2 - Prob. 4CYUCh. 10.2 - Prob. 5CYUCh. 10.2 - Prob. 6CYUCh. 10.2 - Prob. 7CYUCh. 10.2 - Prob. 8CYUCh. 10.2 - Prob. 9CYUCh. 10.2 - Prob. 10CYUCh. 10.2 - Prob. 11CYUCh. 10.2 - Prob. 12CYUCh. 10.2 - Prob. 13CYUCh. 10.2 - Prob. 14PPSCh. 10.2 - Prob. 15PPSCh. 10.2 - Prob. 16PPSCh. 10.2 - Prob. 17PPSCh. 10.2 - Prob. 18PPSCh. 10.2 - Prob. 19PPSCh. 10.2 - Prob. 20PPSCh. 10.2 - Prob. 21PPSCh. 10.2 - Prob. 22PPSCh. 10.2 - Prob. 23PPSCh. 10.2 - Prob. 24PPSCh. 10.2 - Prob. 25PPSCh. 10.2 - Prob. 26PPSCh. 10.2 - Prob. 27PPSCh. 10.2 - Prob. 28PPSCh. 10.2 - Prob. 29PPSCh. 10.2 - Prob. 30PPSCh. 10.2 - Prob. 31PPSCh. 10.2 - Prob. 32PPSCh. 10.2 - Prob. 33PPSCh. 10.2 - Prob. 34PPSCh. 10.2 - Prob. 35PPSCh. 10.2 - Prob. 36PPSCh. 10.2 - Prob. 37PPSCh. 10.2 - Prob. 38PPSCh. 10.2 - Prob. 39PPSCh. 10.2 - Prob. 40PPSCh. 10.2 - Prob. 41PPSCh. 10.2 - Prob. 42PPSCh. 10.2 - Prob. 43PPSCh. 10.2 - Prob. 44PPSCh. 10.2 - Prob. 45PPSCh. 10.2 - Prob. 46PPSCh. 10.2 - Prob. 47PPSCh. 10.2 - Prob. 48PPSCh. 10.2 - Prob. 49PPSCh. 10.2 - Prob. 50PPSCh. 10.2 - Prob. 51PPSCh. 10.2 - Prob. 52PPSCh. 10.2 - Prob. 53HPCh. 10.2 - Prob. 54HPCh. 10.2 - Prob. 55HPCh. 10.2 - Prob. 56HPCh. 10.2 - Prob. 57HPCh. 10.2 - Prob. 58HPCh. 10.2 - Prob. 59HPCh. 10.2 - Prob. 60STPCh. 10.2 - Prob. 61STPCh. 10.2 - Prob. 62STPCh. 10.2 - Prob. 63STPCh. 10.2 - Prob. 64SRCh. 10.2 - Prob. 65SRCh. 10.2 - Prob. 66SRCh. 10.2 - Prob. 67SRCh. 10.2 - Prob. 68SRCh. 10.2 - Prob. 69SRCh. 10.2 - Prob. 70SRCh. 10.2 - Prob. 71SRCh. 10.2 - Prob. 72SRCh. 10.2 - Prob. 73SRCh. 10.2 - Prob. 74SRCh. 10.2 - Prob. 75SCh. 10.2 - Prob. 76SCh. 10.2 - Prob. 77SCh. 10.2 - Prob. 78SCh. 10.2 - Prob. 79SCh. 10.2 - Prob. 80SCh. 10.3 - Prob. 1CYPCh. 10.3 - Prob. 2CYPCh. 10.3 - Prob. 3CYPCh. 10.3 - Prob. 4ACYPCh. 10.3 - Prob. 4BCYPCh. 10.3 - Prob. 1CYUCh. 10.3 - Prob. 2CYUCh. 10.3 - Prob. 3CYUCh. 10.3 - Prob. 4CYUCh. 10.3 - Prob. 5CYUCh. 10.3 - Prob. 6PPSCh. 10.3 - Prob. 7PPSCh. 10.3 - Prob. 8PPSCh. 10.3 - Prob. 9PPSCh. 10.3 - Prob. 10PPSCh. 10.3 - Prob. 11PPSCh. 10.3 - Prob. 12PPSCh. 10.3 - Prob. 13PPSCh. 10.3 - Prob. 14PPSCh. 10.3 - Prob. 15PPSCh. 10.3 - Prob. 16PPSCh. 10.3 - Prob. 17PPSCh. 10.3 - Prob. 18PPSCh. 10.3 - Prob. 19PPSCh. 10.3 - Prob. 20PPSCh. 10.3 - Prob. 21PPSCh. 10.3 - Prob. 22PPSCh. 10.3 - Prob. 23PPSCh. 10.3 - Prob. 24PPSCh. 10.3 - Prob. 25PPSCh. 10.3 - Prob. 26PPSCh. 10.3 - Prob. 27PPSCh. 10.3 - Prob. 28PPSCh. 10.3 - Prob. 29PPSCh. 10.3 - Prob. 30PPSCh. 10.3 - Prob. 31PPSCh. 10.3 - Prob. 32PPSCh. 10.3 - Prob. 33PPSCh. 10.3 - Prob. 34PPSCh. 10.3 - Prob. 35HPCh. 10.3 - Prob. 36HPCh. 10.3 - Prob. 37HPCh. 10.3 - Prob. 38HPCh. 10.3 - Prob. 39HPCh. 10.3 - Prob. 40STPCh. 10.3 - Prob. 41STPCh. 10.3 - Prob. 42STPCh. 10.3 - Prob. 43STPCh. 10.3 - Prob. 44SRCh. 10.3 - Prob. 45SRCh. 10.3 - Prob. 46SRCh. 10.3 - Prob. 47SRCh. 10.3 - Prob. 48SRCh. 10.3 - Prob. 49SRCh. 10.3 - Prob. 50SRCh. 10.3 - Prob. 51SRCh. 10.3 - Prob. 52SRCh. 10.3 - Prob. 53SCh. 10.3 - Prob. 54SCh. 10.3 - Prob. 55SCh. 10.3 - Prob. 56SCh. 10.4 - Prob. 1CYPCh. 10.4 - Prob. 2CYPCh. 10.4 - Prob. 3CYPCh. 10.4 - Prob. 4ACYPCh. 10.4 - Prob. 4BCYPCh. 10.4 - Prob. 1CYUCh. 10.4 - Prob. 2CYUCh. 10.4 - Prob. 3CYUCh. 10.4 - Prob. 4CYUCh. 10.4 - Prob. 5CYUCh. 10.4 - Prob. 6CYUCh. 10.4 - Prob. 7CYUCh. 10.4 - Prob. 8CYUCh. 10.4 - Prob. 9PPSCh. 10.4 - Prob. 10PPSCh. 10.4 - Prob. 11PPSCh. 10.4 - Prob. 12PPSCh. 10.4 - Prob. 13PPSCh. 10.4 - Prob. 14PPSCh. 10.4 - Prob. 15PPSCh. 10.4 - Prob. 16PPSCh. 10.4 - Prob. 17PPSCh. 10.4 - Prob. 18PPSCh. 10.4 - Prob. 19PPSCh. 10.4 - Prob. 20PPSCh. 10.4 - Prob. 21PPSCh. 10.4 - Prob. 22PPSCh. 10.4 - Prob. 23PPSCh. 10.4 - Prob. 24PPSCh. 10.4 - Prob. 25PPSCh. 10.4 - Prob. 26PPSCh. 10.4 - Prob. 27PPSCh. 10.4 - Prob. 28PPSCh. 10.4 - Prob. 29PPSCh. 10.4 - Prob. 30PPSCh. 10.4 - Prob. 31PPSCh. 10.4 - Prob. 32PPSCh. 10.4 - Prob. 33PPSCh. 10.4 - Prob. 34HPCh. 10.4 - Prob. 35HPCh. 10.4 - Prob. 36HPCh. 10.4 - Prob. 37HPCh. 10.4 - Prob. 38HPCh. 10.4 - Prob. 39STPCh. 10.4 - Prob. 40STPCh. 10.4 - Prob. 41STPCh. 10.4 - Prob. 42STPCh. 10.4 - Prob. 43SRCh. 10.4 - Prob. 44SRCh. 10.4 - Prob. 45SRCh. 10.4 - Prob. 46SRCh. 10.4 - Prob. 47SRCh. 10.4 - Prob. 48SRCh. 10.4 - Prob. 49SRCh. 10.4 - Prob. 50SRCh. 10.4 - Prob. 51SCh. 10.4 - Prob. 52SCh. 10.4 - Prob. 53SCh. 10.5 - Prob. 1CYPCh. 10.5 - Prob. 2CYPCh. 10.5 - Prob. 3CYPCh. 10.5 - Prob. 1CYUCh. 10.5 - Prob. 2CYUCh. 10.5 - Prob. 3CYUCh. 10.5 - Prob. 4CYUCh. 10.5 - Prob. 5CYUCh. 10.5 - Prob. 6PPSCh. 10.5 - Prob. 7PPSCh. 10.5 - Prob. 8PPSCh. 10.5 - Prob. 9PPSCh. 10.5 - Prob. 10PPSCh. 10.5 - Prob. 11PPSCh. 10.5 - Prob. 12PPSCh. 10.5 - Prob. 13PPSCh. 10.5 - Prob. 14PPSCh. 10.5 - Prob. 15PPSCh. 10.5 - Prob. 16PPSCh. 10.5 - Prob. 17PPSCh. 10.5 - Prob. 18PPSCh. 10.5 - Prob. 19PPSCh. 10.5 - Prob. 20PPSCh. 10.5 - Prob. 21PPSCh. 10.5 - Prob. 22PPSCh. 10.5 - Prob. 23PPSCh. 10.5 - Prob. 24PPSCh. 10.5 - Prob. 25PPSCh. 10.5 - Prob. 26PPSCh. 10.5 - Prob. 27HPCh. 10.5 - Prob. 28HPCh. 10.5 - Prob. 29HPCh. 10.5 - Prob. 30HPCh. 10.5 - Prob. 31HPCh. 10.5 - Prob. 32STPCh. 10.5 - Prob. 33STPCh. 10.5 - Prob. 34STPCh. 10.5 - Prob. 35STPCh. 10.5 - Prob. 36SRCh. 10.5 - Prob. 37SRCh. 10.5 - Prob. 38SRCh. 10.5 - Prob. 39SRCh. 10.5 - Prob. 40SCh. 10.5 - Prob. 41SCh. 10.5 - Prob. 42SCh. 10.6 - Prob. 1CYPCh. 10.6 - Prob. 2CYPCh. 10.6 - Prob. 3CYPCh. 10.6 - Prob. 1CYUCh. 10.6 - Prob. 2CYUCh. 10.6 - Prob. 3CYUCh. 10.6 - Prob. 4CYUCh. 10.6 - Prob. 5CYUCh. 10.6 - Prob. 6CYUCh. 10.6 - Prob. 7CYUCh. 10.6 - Prob. 8CYUCh. 10.6 - Prob. 9PPSCh. 10.6 - Prob. 10PPSCh. 10.6 - Prob. 11PPSCh. 10.6 - Prob. 12PPSCh. 10.6 - Prob. 13PPSCh. 10.6 - Prob. 14PPSCh. 10.6 - Prob. 15PPSCh. 10.6 - Prob. 16PPSCh. 10.6 - Prob. 17PPSCh. 10.6 - Prob. 18PPSCh. 10.6 - Prob. 19PPSCh. 10.6 - Prob. 20PPSCh. 10.6 - Prob. 21PPSCh. 10.6 - Prob. 22PPSCh. 10.6 - Prob. 23HPCh. 10.6 - Prob. 24HPCh. 10.6 - Prob. 25HPCh. 10.6 - Prob. 26HPCh. 10.6 - Prob. 27HPCh. 10.6 - Prob. 28STPCh. 10.6 - Prob. 29STPCh. 10.6 - Prob. 30STPCh. 10.6 - Prob. 31STPCh. 10.6 - Prob. 32SRCh. 10.6 - Prob. 33SRCh. 10.6 - Prob. 34SRCh. 10.6 - Prob. 35SRCh. 10.6 - Prob. 36SRCh. 10.6 - Prob. 37SRCh. 10.6 - Prob. 38SRCh. 10.6 - Prob. 39SRCh. 10.6 - Prob. 40SRCh. 10.6 - Prob. 41SCh. 10.6 - Prob. 42SCh. 10.6 - Prob. 43SCh. 10.6 - Prob. 44SCh. 10.6 - Prob. 45SCh. 10.6 - Prob. 46SCh. 10.6 - Prob. 47SCh. 10.6 - Prob. 48SCh. 10 - Prob. 1QCCh. 10 - Prob. 2QCCh. 10 - Prob. 3QCCh. 10 - Prob. 4QCCh. 10 - Prob. 5QCCh. 10 - Prob. 6QCCh. 10 - Prob. 7QCCh. 10 - Prob. 8QCCh. 10 - Prob. 9QCCh. 10 - Prob. 10QCCh. 10 - Prob. 11QCCh. 10 - Prob. 12QCCh. 10 - Prob. 13QCCh. 10 - Prob. 14QCCh. 10 - Prob. 15QCCh. 10 - Prob. 16QCCh. 10 - Prob. 17QCCh. 10 - Prob. 18QCCh. 10 - Prob. 19QCCh. 10 - Prob. 20QCCh. 10 - Prob. 1MCQCh. 10 - Prob. 2MCQCh. 10 - Prob. 3MCQCh. 10 - Prob. 4MCQCh. 10 - Prob. 5MCQCh. 10 - Prob. 6MCQCh. 10 - Prob. 7MCQCh. 10 - Prob. 8MCQCh. 10 - Prob. 9MCQCh. 10 - Prob. 10MCQCh. 10 - Prob. 11MCQCh. 10 - Prob. 12MCQCh. 10 - Prob. 13MCQCh. 10 - Prob. 14MCQCh. 10 - Prob. 15MCQCh. 10 - Prob. 16MCQCh. 10 - Prob. 17MCQCh. 10 - Prob. 18MCQCh. 10 - Prob. 19MCQCh. 10 - Prob. 20MCQCh. 10 - Prob. 21MCQCh. 10 - Prob. 22MCQCh. 10 - Prob. 23MCQCh. 10 - Prob. 24MCQCh. 10 - Prob. 25MCQCh. 10 - Prob. 26MCQCh. 10 - Prob. 27MCQCh. 10 - Prob. 28MCQCh. 10 - Prob. 29MCQCh. 10 - Prob. 30MCQCh. 10 - Prob. 31MCQCh. 10 - Prob. 32MCQCh. 10 - Prob. 33MCQCh. 10 - Prob. 1SGRCh. 10 - Prob. 2SGRCh. 10 - Prob. 3SGRCh. 10 - Prob. 4SGRCh. 10 - Prob. 5SGRCh. 10 - Prob. 6SGRCh. 10 - Prob. 7SGRCh. 10 - Prob. 8SGRCh. 10 - Prob. 9SGRCh. 10 - Prob. 10SGRCh. 10 - Prob. 11SGRCh. 10 - Prob. 12SGRCh. 10 - Prob. 13SGRCh. 10 - Prob. 14SGRCh. 10 - Prob. 15SGRCh. 10 - Prob. 16SGRCh. 10 - Prob. 17SGRCh. 10 - Prob. 18SGRCh. 10 - Prob. 19SGRCh. 10 - Prob. 20SGRCh. 10 - Prob. 21SGRCh. 10 - Prob. 22SGRCh. 10 - Prob. 23SGRCh. 10 - Prob. 24SGRCh. 10 - Prob. 25SGRCh. 10 - Prob. 26SGRCh. 10 - Prob. 27SGRCh. 10 - Prob. 28SGRCh. 10 - Prob. 29SGRCh. 10 - Prob. 30SGRCh. 10 - Prob. 31SGRCh. 10 - Prob. 32SGRCh. 10 - Prob. 33SGRCh. 10 - Prob. 34SGRCh. 10 - Prob. 35SGRCh. 10 - Prob. 36SGRCh. 10 - Prob. 37SGRCh. 10 - Prob. 38SGRCh. 10 - Prob. 39SGRCh. 10 - Prob. 40SGRCh. 10 - Prob. 41SGRCh. 10 - Prob. 42SGRCh. 10 - Prob. 43SGRCh. 10 - Prob. 44SGRCh. 10 - Prob. 45SGRCh. 10 - Prob. 46SGRCh. 10 - Prob. 47SGRCh. 10 - Prob. 48SGRCh. 10 - Prob. 49SGRCh. 10 - Prob. 50SGRCh. 10 - Prob. 51SGRCh. 10 - Prob. 1PTCh. 10 - Prob. 2PTCh. 10 - Prob. 3PTCh. 10 - Prob. 4PTCh. 10 - Prob. 5PTCh. 10 - Prob. 6PTCh. 10 - Prob. 7PTCh. 10 - Prob. 8PTCh. 10 - Prob. 9PTCh. 10 - Prob. 10PTCh. 10 - Prob. 11PTCh. 10 - Prob. 12PTCh. 10 - Prob. 13PTCh. 10 - Prob. 14PTCh. 10 - Prob. 15PTCh. 10 - Prob. 16PTCh. 10 - Prob. 17PTCh. 10 - Prob. 18PTCh. 10 - Prob. 19PTCh. 10 - Prob. 20PTCh. 10 - Prob. 21PTCh. 10 - Prob. 22PTCh. 10 - Prob. 23PTCh. 10 - Prob. 24PTCh. 10 - Prob. 25PTCh. 10 - Prob. 1ECh. 10 - Prob. 2ECh. 10 - Prob. 1STPCh. 10 - Prob. 2STPCh. 10 - Prob. 3STPCh. 10 - Prob. 4STPCh. 10 - Prob. 5STPCh. 10 - Prob. 6STPCh. 10 - Prob. 7STPCh. 10 - Prob. 8STPCh. 10 - Prob. 9STPCh. 10 - Prob. 10STPCh. 10 - Prob. 11STP
Additional Math Textbook Solutions
Find more solutions based on key concepts
Ages A study of all the students at a small college showed a mean age of 20.7 and a standard deviation of 2.5 y...
Introductory Statistics
Calculating derivatives Find dy/dx for the following functions. 21. y = x sin x
Calculus: Early Transcendentals (2nd Edition)
Assessment 1-1A In a big red box, there are 7 smaller blue boxes. In each of the blue boxes, there are 7 black ...
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Fill in each blank so that the resulting statement is true. Any set of ordered pairs is called a/an ____.The se...
Algebra and Trigonometry (6th Edition)
76. Dew Point and Altitude The dew point decreases as altitude increases. If the dew point on the ground is 80°...
College Algebra with Modeling & Visualization (5th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Similar questions
- - Consider the following system of linear equations in the variables a,b,c,d: 5a-3b 7c - 2d = 2 2ab 2c+ 5d = -3 → (*) 4a 3b 5d = 3 6a b+2c+ 7d = −7 (a) Solve the system (*) by using Gauss elimination method. (b) Solve the system (*) by using Cramer's rule method.arrow_forwardSolve for a 25 55 30 a=?arrow_forward9:41 … 93 Applying an Exponential Function to Newton's Law of Cooling 60. Water in a water heater is originally Aa ← 122°F. The water heater is shut off and the water cools to the temperature of the surrounding air, which is 60°F. The water cools slowly because of the insulation inside the heater, and the value of k is measured as 0.00351. a. Write a function that models the temperature T (t) (in °F) of the water t hours after the water heater is shut off. b. What is the temperature of the water 12 hr after the heater is shut off? Round to the nearest degree. c. Dominic does not like to shower with water less than 115°F. If Dominic waits 24 hr. will the water still be warm enough for a shower? Mixed Exercises ger-ui.prod.mheducation.comarrow_forward
- Please use the infinite series formula and specify how you did each step. Thank you.arrow_forward8) Solve the given system using the Gaussian Elimination process. 2x8y = 3 (-6x+24y = −6arrow_forward7) Solve the given system using the Gaussian Elimination process. (5x-4y = 34 (2x - 2y = 14arrow_forward
- 33 (a) (b) Let A(t) = = et 0 0 0 cos(t) sin(t) 0-sin(t) cos(t)) For any fixed tЄR, find det(A(t)). Show that the matrix A(t) is invertible for any tЄ R, and find the inverse (A(t))¹.arrow_forwardUse the infinite geometric sum to convert .258 (the 58 is recurring, so there is a bar over it) to a ratio of two integers. Please go over the full problem, specifying how you found r. Thank you.arrow_forwardH.w: Find the Eigen vectors for the largest Eigen value of the system X1+ +2x3=0 3x1-2x2+x3=0 4x1+ +3x3=0arrow_forward
- need help with 5 and 6 pleasearrow_forward1) Given matrix A below, answer the following questions: a) What is the order of the matrix? b) What is the element a13? c) What is the element a₁₁? 4 -1arrow_forward[25 points] Given the vector let v = ER² and the collection of vectors ε = E-{)·()}-{☹) (9)} = {(A)·(9)}· B: = and C = · {(6)·(})}· answer the following question. (a) (b) (c) (d) (e) verify Verify is a basis for R² and find the coordinate [] of under ε. Verify B is a basis for R2 and find the coordinate []B of ʊ Verify C is a basis for R2 and find the coordinate []c of under ε. under ε. Find the change-of-basis matrix [I]+B from basis B to basis ε, and EE+BUB Find the change-of-basis matrix [I]B+ε from basis Ɛ to basis B, and verify [U]B= [] B+EVEarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
Algebra and Trigonometry (6th Edition)
Algebra
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:PEARSON
Contemporary Abstract Algebra
Algebra
ISBN:9781305657960
Author:Joseph Gallian
Publisher:Cengage Learning
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Algebra And Trigonometry (11th Edition)
Algebra
ISBN:9780135163078
Author:Michael Sullivan
Publisher:PEARSON
Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:9780980232776
Author:Gilbert Strang
Publisher:Wellesley-Cambridge Press
College Algebra (Collegiate Math)
Algebra
ISBN:9780077836344
Author:Julie Miller, Donna Gerken
Publisher:McGraw-Hill Education
Whiteboard Math: The Basics of Factoring; Author: Whiteboard Math;https://www.youtube.com/watch?v=-VKAYqzRp4o;License: Standard YouTube License, CC-BY
Factorisation using Algebraic Identities | Algebra | Mathacademy; Author: Mathacademy;https://www.youtube.com/watch?v=BEp1PaU-qEw;License: Standard YouTube License, CC-BY
How To Factor Polynomials The Easy Way!; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=U6FndtdgpcA;License: Standard Youtube License