INTERNATIONAL EDITION---Engineering Mechanics: Statics, 14th edition (SI unit)
14th Edition
ISBN: 9780133918922
Author: Russell C. Hibbeler
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 10.3, Problem 1FP
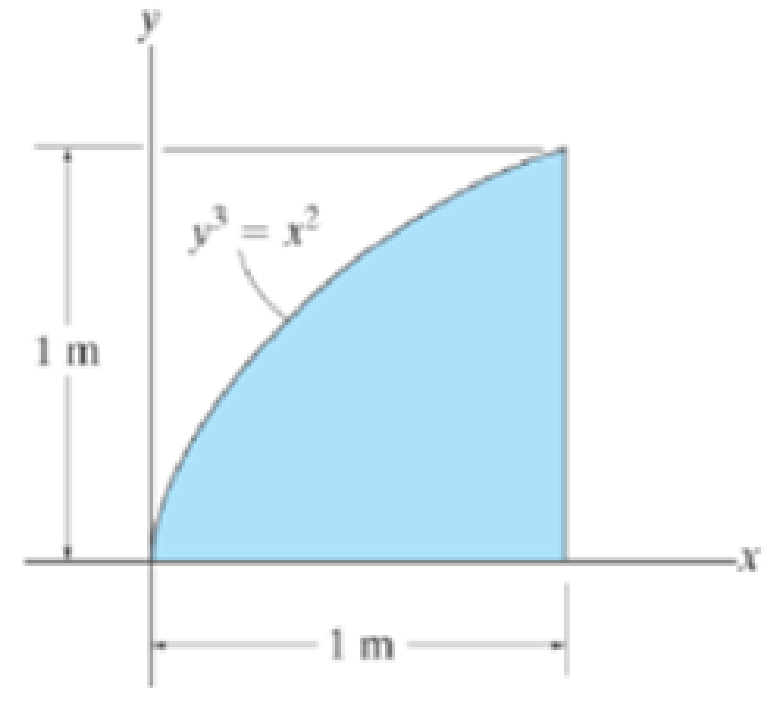
Determine the moment of inertia of the shaded area about the x axis.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
A boiler with 80% efficiency produces steam at 40bar and 500 C at a rate of 1.128kg/s.
The temperature of the feed water is raised from 25 C to 125 C in the economizer and the
ambient air is drawn to the boiler at a rate of 2.70 kg/s at 16 C. The flue gases leave the
chimney at rate of 3 kg/s at 150 C with specific heat of 1.01 kJ/kg.K. The dryness fraction
of steam collected in the steam drum is 0.95.
1- Determine the heat value of the fuel.
2- The equivalence evaporation.
3- Draw the heat balance sheet.
A rotating shaft is made of 42 mm by 4 mm thick cold-drawn round steel tubing and has a 6 mm diameter
hole drilled transversely through it. The shaft is subjected to a pulsating torque fluctuating from 20 to 160
Nm and a completely reversed bending moment of 200 Nm. The steel tubing has a minimum strength of Sut
= 410 MPa (60 ksi). The static stress-concentration factor for the hole is 2.4 for bending and 1.9 for torsion.
The maximum operating temperature is 400˚C and a reliability of 99.9% is to be assumed. Find the factor of
safety for infinite life using the modified Goodman failure criterion.
I need help with a MATLAB code. This code just keeps running and does not give me any plots. I even reduced the tolerance from 1e-9 to 1e-6. Can you help me fix this? Please make sure your solution runs.
% Initial Conditions
rev = 0:0.001:2;
g1 = deg2rad(1);
g2 = deg2rad(3);
g3 = deg2rad(6);
g4 = deg2rad(30);
g0 = deg2rad(0);
Z0 = 0;
w0 = [0; Z0*cos(g0); -Z0*sin(g0)];
Z1 = 5;
w1 = [0; Z1*cos(g1); -Z1*sin(g1)];
Z2 = 11;
w2 = [0; Z2*cos(g2); -Z2*sin(g2)];
[v3, psi3, eta3] = Nut_angle(Z2, g2, w2);
plot(v3, psi3)
function dwedt = K_DDE(~, w_en)
% Extracting the initial condtions to a variable
% Extracting the initial condtions to a variable
w = w_en(1:3);
e = w_en(4:7);
Z = w_en(8);
I = 0.060214;
J = 0.015707;
x = (J/I) - 1;
y = Z - 1;
s = Z;
% Kinematic Differential Equations
dedt = zeros(4,1);
dedt(1) = pi*(e(3)*(s-w(2)-1) + e(2)*w(3) + e(4)*w(1));
dedt(2) = pi*(e(4)*(w(2)-1-s) + e(3)*w(1) - e(1)*w(3));
dedt(3) = pi*(-e(1)*(s-w(2)-1) - e(2)*w(1) + e(4)*w(3));…
Chapter 10 Solutions
INTERNATIONAL EDITION---Engineering Mechanics: Statics, 14th edition (SI unit)
Ch. 10.3 - Determine the moment of inertia of the shaded area...Ch. 10.3 - Determine the moment of inertia of the shaded area...Ch. 10.3 - Determine the moment of inertia of the shaded area...Ch. 10.3 - Determine the moment of inertia of the shaded area...Ch. 10.3 - Determine the moment of inertia about the x axis.Ch. 10.3 - Determine the moment of inertia about the y axis.Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Determine the moment of Inertia for the shaded...Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Determine the moment of inertia for the shaded...
Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Solve the problem in two ways, using rectangular...Ch. 10.3 - Determine the moment of inertia of the area about...Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Determine the moment of inertia about the x axis.Ch. 10.3 - Determine the moment of inertia about the y axis.Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Prob. 23PCh. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.4 - Determine the moment of inertia of the beams...Ch. 10.4 - Determine the moment of inertia of the beams...Ch. 10.4 - Determine me moment of inertia of the...Ch. 10.4 - Determine the moment of inertia of the...Ch. 10.4 - Determine the moment of inertia of the composite...Ch. 10.4 - Determine the moment of inertia of the composite...Ch. 10.4 - The moment of inertia about the y axis is 264...Ch. 10.4 - Determine the location y of the centroid of the...Ch. 10.4 - Determine,y, which locates the centroidal axis x...Ch. 10.4 - Determine the moment of inertia for the beams...Ch. 10.4 - Determine the moment of inertia for the beams...Ch. 10.4 - Determine the moment of inertia Ix of the shaded...Ch. 10.4 - Determine the moment of inertia Ix of the shaded...Ch. 10.4 - Determine the moment of inertia of the beams...Ch. 10.4 - Determine, g, which locates the centroidal axis z...Ch. 10.4 - Determine the moment of inertia about the x axis.Ch. 10.4 - Prob. 37PCh. 10.4 - Determine the moment of inertia of the shaded area...Ch. 10.4 - Determine the moment of inertia of the shaded area...Ch. 10.4 - Prob. 40PCh. 10.4 - Prob. 41PCh. 10.4 - Determine the moment of inertia of the beams...Ch. 10.4 - Prob. 43PCh. 10.4 - Prob. 44PCh. 10.4 - Determine the distance x to the centroid C of the...Ch. 10.4 - Determine the moment of inertia for the shaded...Ch. 10.4 - Determine the moment of inertia for the shaded...Ch. 10.4 - Determine the moment of inertia of the...Ch. 10.4 - Determine the moment of inertia of the...Ch. 10.4 - Prob. 50PCh. 10.4 - Determine the moment of inertia for the beams...Ch. 10.4 - Determine the moment of inertia of the area about...Ch. 10.4 - Determine the moment of inertia of the area about...Ch. 10.7 - Determine the product of inertia of the thin strip...Ch. 10.7 - Determine the product of inertia of the shaded...Ch. 10.7 - Determine the product of inertia for the shaded...Ch. 10.7 - Determine the product of inertia of the shaded...Ch. 10.7 - Determine the product of inertia for the parabolic...Ch. 10.7 - Prob. 59PCh. 10.7 - Determine the product of inertia of the shaded...Ch. 10.7 - Prob. 61PCh. 10.7 - Prob. 62PCh. 10.7 - Prob. 63PCh. 10.7 - Determine the product of inertia for the beams...Ch. 10.7 - Determine the product of inertia tor the shaded...Ch. 10.7 - Determine the product of inertia of the cross...Ch. 10.7 - Determine the location (xy) to the centroid C of...Ch. 10.7 - For the calculation, assume all comers to be...Ch. 10.7 - Determine the moments of inertia Iu, Iv and the...Ch. 10.7 - Prob. 70PCh. 10.7 - using Mohrs circle Hint. To solve find the...Ch. 10.7 - Prob. 72PCh. 10.7 - using Mohrs circle.Ch. 10.7 - Prob. 74PCh. 10.7 - using Mohrs circle.Ch. 10.7 - Prob. 76PCh. 10.7 - using Mohrs circle.Ch. 10.7 - Prob. 78PCh. 10.7 - using Mohrs circle.Ch. 10.7 - Prob. 80PCh. 10.7 - Solve Prob. 10-80 using Mohrs circle.Ch. 10.7 - Prob. 82PCh. 10.7 - Solve Prob. 10-82 using Mohrs circle.Ch. 10.8 - Determine the moment of inertia of the thin ring...Ch. 10.8 - The material has a constant density .Ch. 10.8 - Determine the radius of gyration kx of the...Ch. 10.8 - Prob. 87PCh. 10.8 - Hint: For integration, use thin plate elements...Ch. 10.8 - The material has a constant density .Ch. 10.8 - Prob. 90PCh. 10.8 - Determine the moment of inertia Iy. The specific...Ch. 10.8 - Prob. 92PCh. 10.8 - Prob. 93PCh. 10.8 - The total mass of the solid is 1500 kg.Ch. 10.8 - The slender rods have a mass of 4 kg/ point A....Ch. 10.8 - and a 4-kg slender rod. Determine the radius of...Ch. 10.8 - The material has a density of 200kg/m3. Prob....Ch. 10.8 - Determine the location y of the center of mass G...Ch. 10.8 - Prob. 99PCh. 10.8 - The pendulum consists of a plate having a weight...Ch. 10.8 - 15 lb. and 20 lb, respectively, determine the mass...Ch. 10.8 - The density of the material is 7.85 Mg/m3.Ch. 10.8 - Prob. 103PCh. 10.8 - Determine its mass moment of inertia about the y...Ch. 10.8 - Prob. 105PCh. 10.8 - Prob. 106PCh. 10.8 - Prob. 107PCh. 10.8 - The thin plate has a mass of 12 kg/m2. Determine...Ch. 10.8 - The material has a density of 200kg/m3.Ch. 10.8 - Determine the moment of inertia for the shaded...Ch. 10.8 - Determine the moment of inertia for the shaded...Ch. 10.8 - Determine the area moment of inertia of the shaded...Ch. 10.8 - Prob. 4RPCh. 10.8 - Determine the area moment of inertia of the...Ch. 10.8 - Determine the product of inertia of the shaded...
Additional Engineering Textbook Solutions
Find more solutions based on key concepts
What output will the following lines of code display on the screen? cout "The works of Wolfgang\ninclude the f...
Starting Out with C++: Early Objects (9th Edition)
A nozzle at A discharges water with an initial velocity of 36 ft/s at an angle with the horizontal. Determine ...
Vector Mechanics For Engineers
CONCEPT QUESTIONS
15.CQ3 The ball rolls without slipping on the fixed surface as shown. What is the direction ...
Vector Mechanics for Engineers: Statics and Dynamics
Computers process data under the control of sets of instructions called
Java How to Program, Early Objects (11th Edition) (Deitel: How to Program)
How is the hydrodynamic entry length defined for flow in a pipe? Is the entry length longer in laminar or turbu...
Fluid Mechanics: Fundamentals and Applications
1.2 Explain the difference between geodetic and plane
surveys,
Elementary Surveying: An Introduction To Geomatics (15th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- alpha 1 is not zero alpha 1 can equal alpha 2 use velocity triangle to solve for alpha 1 USE MATLAB ONLY provide typed code solve for velocity triangle and dont provide copied answer Turbomachienery . GIven: vx = 185 m/s, flow angle = 60 degrees, (leaving a stator in axial flow) R = 0.5, U = 150 m/s, b2 = -a3, a2 = -b3 Find: velocity triangle , a. magnitude of abs vel leaving rotor (m/s) b. flow absolute angles (a1, a2, a3) 3. flow rel angles (b2, b3) d. specific work done e. use code to draw vel. diagram Use this code for plot % plots Velocity Tri. in Ch4 function plotveltri(al1,al2,al3,b2,b3) S1L = [0 1]; V1x = [0 0]; V1s = [0 1*tand(al3)]; S2L = [2 3]; V2x = [0 0]; V2s = [0 1*tand(al2)]; W2s = [0 1*tand(b2)]; U2x = [3 3]; U2y = [1*tand(b2) 1*tand(al2)]; S3L = [4 5]; V3x = [0 0]; V3r = [0 1*tand(al3)]; W3r = [0 1*tand(b3)]; U3x = [5 5]; U3y = [1*tand(b3) 1*tand(al3)]; plot(S1L,V1x,'k',S1L,V1s,'r',... S2L,V2x,'k',S2L,V2s,'r',S2L,W2s,'b',U2x,U2y,'g',...…arrow_forward3. Find a basis of eigenvectors and diagonalize. 4 0 -19 7 a. b. 1-42 16 12-20 [21-61arrow_forward2. Find the eigenvalues. Find the corresponding eigenvectors. 6 2 -21 [0 -3 1 3 31 a. 2 5 0 b. 3 0 -6 C. 1 1 0 -2 0 7 L6 6 0 1 1 2. (Hint: λ = = 3)arrow_forward
- USE MATLAB ONLY provide typed code solve for velocity triangle and dont provide copied answer Turbomachienery . GIven: vx = 185 m/s, flow angle = 60 degrees, (leaving a stator in axial flow) R = 0.5, U = 150 m/s, b2 = -a3, a2 = -b3 Find: velocity triangle , a. magnitude of abs vel leaving rotor (m/s) b. flow absolute angles (a1, a2, a3) 3. flow rel angles (b2, b3) d. specific work done e. use code to draw vel. diagram Use this code for plot % plots Velocity Tri. in Ch4 function plotveltri(al1,al2,al3,b2,b3) S1L = [0 1]; V1x = [0 0]; V1s = [0 1*tand(al3)]; S2L = [2 3]; V2x = [0 0]; V2s = [0 1*tand(al2)]; W2s = [0 1*tand(b2)]; U2x = [3 3]; U2y = [1*tand(b2) 1*tand(al2)]; S3L = [4 5]; V3x = [0 0]; V3r = [0 1*tand(al3)]; W3r = [0 1*tand(b3)]; U3x = [5 5]; U3y = [1*tand(b3) 1*tand(al3)]; plot(S1L,V1x,'k',S1L,V1s,'r',... S2L,V2x,'k',S2L,V2s,'r',S2L,W2s,'b',U2x,U2y,'g',... S3L,V3x,'k',S3L,V3r,'r',S3L,W3r,'b',U3x,U3y,'g',...... 'LineWidth',2,'MarkerSize',10),...…arrow_forwardUSE MATLAB ONLY provide typed code solve for velocity triangle and dont provide copied answer Turbomachienery . GIven: vx = 185 m/s, flow angle = 60 degrees, R = 0.5, U = 150 m/s, b2 = -a3, a2 = -b3 Find: velocity triangle , a. magnitude of abs vel leaving rotor (m/s) b. flow absolute angles (a1, a2, a3) 3. flow rel angles (b2, b3) d. specific work done e. use code to draw vel. diagram Use this code for plot % plots Velocity Tri. in Ch4 function plotveltri(al1,al2,al3,b2,b3) S1L = [0 1]; V1x = [0 0]; V1s = [0 1*tand(al3)]; S2L = [2 3]; V2x = [0 0]; V2s = [0 1*tand(al2)]; W2s = [0 1*tand(b2)]; U2x = [3 3]; U2y = [1*tand(b2) 1*tand(al2)]; S3L = [4 5]; V3x = [0 0]; V3r = [0 1*tand(al3)]; W3r = [0 1*tand(b3)]; U3x = [5 5]; U3y = [1*tand(b3) 1*tand(al3)]; plot(S1L,V1x,'k',S1L,V1s,'r',... S2L,V2x,'k',S2L,V2s,'r',S2L,W2s,'b',U2x,U2y,'g',... S3L,V3x,'k',S3L,V3r,'r',S3L,W3r,'b',U3x,U3y,'g',...... 'LineWidth',2,'MarkerSize',10),... axis([-1 6 -4 4]), ...…arrow_forwardThe answer should equal to 1157. Please sent me the solution. Thank you!arrow_forward
- BONUS: If the volume of the 8cm x 6.5cm x 6cm Block of Aluminum was 312cm3 before machining, find how much material was removed when the fixture below was machined. +2 2.00 cm 6.00 cm 2.50 cm 6.50 cm 1.00 cm 2.50 cm 11.00 cm 8.00 cm 30 CP 9411 FL.4) (m² 1157 Area of triangle = 1/2*B*H Area of circle = лR² Circumference of a circle = 2πR 6.00 cm 6.50 cm 1.50 cm Radius 1.50 cm 1.00 cmarrow_forwardConsider a 5m by 5m wet concret patio with an average water film thickness of .2mm. Now wind at 50 km/h is blowing over the surface. If the air is at 1 atm, 15oC and 35 percent relative humidity, determine how long it will take for the patio to completely dry.arrow_forward70. Compute the number of cubic centimeters of iron required for the cast-iron plate shown. The plate is 3.50 centimeters thick. Round the answer to the nearest cubic centimeter. 50.0 cm 40.0 cm Radius 150° 115.0 cm- 81.0 cmarrow_forward
- Law of Sines Solve the following problems using the Law of Sin 7. Find side x. All dimensions are in inches. -°-67°-37° 81° x Sin A 8.820 X 67°00' 32°00' a sin A b C sin B sin Carrow_forward35. a. Determine B. b. Determine side b. c. Determine side c. 5.330 in.- ZB 73°30'arrow_forwardConsider a 12 cm internal diameter, 14 m long circular duct whose interior surface is wet. The duct is to be dried by forcing dry air at 1 atm and 15 degrees C throught it at an average velocity of 3m/s. The duct passes through a chilled roo, and it remains at an average temp of 15 degrees C at all time. Determine the mass transfer coeeficient in the duct.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Elements Of Electromagnetics
Mechanical Engineering
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Oxford University Press
Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:9780134319650
Author:Russell C. Hibbeler
Publisher:PEARSON
Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:9781259822674
Author:Yunus A. Cengel Dr., Michael A. Boles
Publisher:McGraw-Hill Education
Control Systems Engineering
Mechanical Engineering
ISBN:9781118170519
Author:Norman S. Nise
Publisher:WILEY
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
Engineering Mechanics: Statics
Mechanical Engineering
ISBN:9781118807330
Author:James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:WILEY
moment of inertia; Author: NCERT OFFICIAL;https://www.youtube.com/watch?v=A4KhJYrt4-s;License: Standard YouTube License, CC-BY