Precalculus
Precalculus
17th Edition
ISBN: 9780078035609
Author: Miller, Julie, Gerken, Donna.
Publisher: Mcgraw-hill Education,
bartleby

Videos

Textbook Question
Book Icon
Chapter 10.2, Problem 81PE

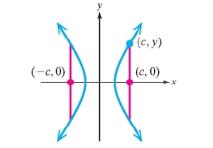
A line segment with endpoints on a hyperbola, perpendicular to the transverse axis, and passing through a focus is called a latus rectum of the hyperbola (shown in red). Show that the length of a latus rectum is 2 b 2 a for the hyperbola

x 2 a 2 − y 2 b 2 = 1

Chapter 10.2, Problem 81PE, A line segment with endpoints on a hyperbola, perpendicular to the transverse axis, and passing

Expert Solution & Answer
Check Mark
bartleby

Trending nowThis is a popular solution!

See solution
Check out sample textbook solution
Blurred answer
Previous
Chapter 10.2, Problem 80PE
Next
Chapter 10.2, Problem 82PE
Students have asked these similar questions
Find the volume of the parallelepiped determined by the vectors a = (3, 5, −1), ☎ = (0, 3, 1), c = (2,4,1).
Find the area of a triangle PQR, where P = (-5,6, -1), Q = (1, -3, -2), and R = (-5, -1,4)
17. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.2.050. Evaluate the integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) du 4√3- -4² Need Help? Read It SUBMIT ANSWER 18. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.2.051. Evaluate the integral. (Use C for the constant of integration.) - 49 dx x² +3 Need Help? Read It Watch It SUBMIT ANSWER 19. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.2.057. Evaluate the integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) 25+ x2 dx

Chapter 10 Solutions

Precalculus

Ch. 10.1 - Graph the ellipse, and identify the center,...Ch. 10.1 - Graph the ellipse and identify the center,...Ch. 10.1 - Graph the ellipse and identify the center,...Ch. 10.1 - Repeat Example 4 with 2x2+11y212x+44y+40=0 .Ch. 10.1 - Determine the standard form of an equation of an...Ch. 10.1 - A tunnel has vertical sides of 7 ft with a...Ch. 10.1 - Pluto is 7.376109 km at aphelion (farthest point...Ch. 10.1 - The circle, the ellipse, the hyperbola, and the...Ch. 10.1 - An is a set of points x,y in a plane such that...Ch. 10.1 - The line through the foci intersects an ellipse at...
Ch. 10.1 - The line segment with endpoints at the vertices of...Ch. 10.1 - The line segment perpendicular to the major axis,...Ch. 10.1 - Given x2a2+y2b2=1, where ab0, the ordered pairs...Ch. 10.1 - Given xh2b2+yk2a2=1, where ab0, the ordered pairs...Ch. 10.1 - When referring to the standard form of an equation...Ch. 10.1 - For Exercises 9-10, a. Use the distance formula to...Ch. 10.1 - For Exercises 9-10, a. Use the distance formula to...Ch. 10.1 - For Exercises 11-12, from the equation of the...Ch. 10.1 - For Exercises 11-12, from the equation of the...Ch. 10.1 - For Exercises 13-22, a. Identify the center of the...Ch. 10.1 - For Exercises 13-22, a. Identify the center of the...Ch. 10.1 - For Exercises 13-22, a. Identify the center of the...Ch. 10.1 - For Exercises 13-22, a. Identify the center of the...Ch. 10.1 - For Exercises 13-22, a. Identify the center of the...Ch. 10.1 - For Exercises 13-22, a. Identify the center of the...Ch. 10.1 - Prob. 19PECh. 10.1 - For Exercises 13-22, a. Identify the center of the...Ch. 10.1 - Prob. 21PECh. 10.1 - For Exercises 13-22, a. Identify the center of the...Ch. 10.1 - Prob. 23PECh. 10.1 - Prob. 24PECh. 10.1 - For Exercises 23-32, a. Identify the center of the...Ch. 10.1 - For Exercises 23-32, a. Identify the center of the...Ch. 10.1 - Prob. 27PECh. 10.1 - For Exercises 23-32, a. Identify the center of the...Ch. 10.1 - Prob. 29PECh. 10.1 - For Exercises 23-32, a. Identify the center of the...Ch. 10.1 - For Exercises 23-32, a. Identify the center of the...Ch. 10.1 - For Exercises 23-32, a. Identify the center of the...Ch. 10.1 - For Exercises 33-42, a. Write the equation of the...Ch. 10.1 - For Exercises 33-42, a. Write the equation of the...Ch. 10.1 - For Exercises 33-42, a. Write the equation of the...Ch. 10.1 - Prob. 36PECh. 10.1 - Prob. 37PECh. 10.1 - Prob. 38PECh. 10.1 - For Exercises 33-42, a. Write the equation of the...Ch. 10.1 - Prob. 40PECh. 10.1 - Prob. 41PECh. 10.1 - For Exercises 33-42, a. Write the equation of the...Ch. 10.1 - Prob. 43PECh. 10.1 - Prob. 44PECh. 10.1 - For Exercises 43-56, write the standard form of an...Ch. 10.1 - Prob. 46PECh. 10.1 - For Exercises 43-56, write the standard form of an...Ch. 10.1 - Prob. 48PECh. 10.1 - For Exercises 43-56, write the standard form of an...Ch. 10.1 - Prob. 50PECh. 10.1 - For Exercises 43-56, write the standard form of an...Ch. 10.1 - Prob. 52PECh. 10.1 - Prob. 53PECh. 10.1 - For Exercises 43-56, write the standard form of an...Ch. 10.1 - For Exercises 43-56, write the standard form of an...Ch. 10.1 - For Exercises 43-56, write the standard form of an...Ch. 10.1 - The reflective property of an ellipse is used in...Ch. 10.1 - The reflective property of an ellipse is the...Ch. 10.1 - A homeowner wants to make an elliptical rug from a...Ch. 10.1 - Prob. 60PECh. 10.1 - Charles and Bernice (“Ray") Eames were American...Ch. 10.1 - A window above a door is to be made in the shape...Ch. 10.1 - Prob. 63PECh. 10.1 - Choose one: An ellipse with eccentricity close to...Ch. 10.1 - Choose one: An ellipse with eccentricity close to...Ch. 10.1 - Choose one: If the foci of an ellipse are close to...Ch. 10.1 - For Exercises 67-72, determine the eccentricity of...Ch. 10.1 - For Exercises 67-72, determine the eccentricity of...Ch. 10.1 - Prob. 69PECh. 10.1 - For Exercises 67-72, determine the eccentricity of...Ch. 10.1 - For Exercises 67-72, determine the eccentricity of...Ch. 10.1 - For Exercises 67-72, determine the eccentricity of...Ch. 10.1 - Halley's Comet and the Earth both orbit the Sun in...Ch. 10.1 - Halley's Comet and the comet Hale-Bopp both orbit...Ch. 10.1 - The moon's orbit around the Earth is elliptical...Ch. 10.1 - The planet Saturn orbits the Sun in an elliptical...Ch. 10.1 - The Roman Coliseum is an elliptical stone and...Ch. 10.1 - The Ellipse, also called Presidents Park South, is...Ch. 10.1 - Prob. 79PECh. 10.1 - For Exercises 79-82, write the standard form of an...Ch. 10.1 - For Exercises 79-82, write the standard form of an...Ch. 10.1 - Prob. 82PECh. 10.1 - A circular vent pipe is placed on a flat roof. a....Ch. 10.1 - A cylindrical glass of water with diameter 3.5in....Ch. 10.1 - Prob. 85PECh. 10.1 - The graph of x216+y281=1 represents an ellipse....Ch. 10.1 - For Exercises 87-90, solve the system of...Ch. 10.1 - Prob. 88PECh. 10.1 - For Exercises 87-90, solve the system of...Ch. 10.1 - For Exercises 87-90, solve the system of...Ch. 10.1 - Given an ellipse with major axis of length 2a and...Ch. 10.1 - Prob. 92PECh. 10.1 - A line segment with endpoints on an ellipse,...Ch. 10.1 - Prob. 94PECh. 10.1 - Prob. 95PECh. 10.1 - Given an equation of an ellipse in standard form,...Ch. 10.1 - Explain the difference between the graphs of the...Ch. 10.1 - Discuss the solution set of the equation....Ch. 10.1 - This exercise guides you through the steps to find...Ch. 10.1 - Find the points on the ellipse that are twice the...Ch. 10.1 - Prob. 101PECh. 10.1 - Prob. 102PECh. 10.1 - For Exercises 102-105, graph the ellipse from the...Ch. 10.1 - For Exercises 102-105, graph the ellipse from the...Ch. 10.1 - For Exercises 102-105, graph the ellipse from the...Ch. 10.2 - Repeat Example 1 with the equation: x29y24=1Ch. 10.2 - Prob. 2SPCh. 10.2 - Repeat Example 3 with the equation: x+124+y4225=1Ch. 10.2 - Prob. 4SPCh. 10.2 - Prob. 5SPCh. 10.2 - Determine the eccentricity of the hyperbola....Ch. 10.2 - Prob. 7SPCh. 10.2 - A is the set of points x,y in a plane such that...Ch. 10.2 - The points where a hyperbola intersects the line...Ch. 10.2 - Prob. 3PECh. 10.2 - Prob. 4PECh. 10.2 - The equation x2a2y2b2=1 represents a hyperbola...Ch. 10.2 - The equation y2a2x2b2=1 represents a hyperbola...Ch. 10.2 - For Exercises 7-8, a. Use the distance formula to...Ch. 10.2 - For Exercises 7-8, a. Use the distance formula to...Ch. 10.2 - For Exercises 9-12, determine whether the...Ch. 10.2 - For Exercises 9-12, determine whether the...Ch. 10.2 - For Exercises 9-12, determine whether the...Ch. 10.2 - Prob. 12PECh. 10.2 - Prob. 13PECh. 10.2 - For Exercises 13-22, a. Identify the center. b....Ch. 10.2 - For Exercises 13-22, a. Identify the center. b....Ch. 10.2 - For Exercises 13-22, a. Identify the center. b....Ch. 10.2 - Prob. 17PECh. 10.2 - For Exercises 13-22, a. Identify the center. b....Ch. 10.2 - Prob. 19PECh. 10.2 - For Exercises 13-22, a. Identify the center. b....Ch. 10.2 - Prob. 21PECh. 10.2 - For Exercises 13-22, a. Identify the center. b....Ch. 10.2 - For Exercises 23-32, a. Identify1he center. b....Ch. 10.2 - For Exercises 23-32, a. Identify1he center. b....Ch. 10.2 - Prob. 25PECh. 10.2 - For Exercises 23-32, a. Identify1he center. b....Ch. 10.2 - For Exercises 23-32, a. Identify1he center. b....Ch. 10.2 - Prob. 28PECh. 10.2 - For Exercises 23-32, a. Identify1he center. b....Ch. 10.2 - Prob. 30PECh. 10.2 - Prob. 31PECh. 10.2 - For Exercises 23-32, a. Identify1he center. b....Ch. 10.2 - For Exercises 33-40, a. Write the equation of the...Ch. 10.2 - For Exercises 33-40, a. Write the equation of the...Ch. 10.2 - For Exercises 33-40, a. Write the equation of the...Ch. 10.2 - For Exercises 33-40, a. Write the equation of the...Ch. 10.2 - Prob. 37PECh. 10.2 - Prob. 38PECh. 10.2 - For Exercises 33-40, a. Write the equation of the...Ch. 10.2 - For Exercises 33-40, a. Write the equation of the...Ch. 10.2 - For Exercises 41-50, write the standard form of...Ch. 10.2 - For Exercises 41-50, write the standard form of...Ch. 10.2 - Prob. 43PECh. 10.2 - Prob. 44PECh. 10.2 - Prob. 45PECh. 10.2 - Prob. 46PECh. 10.2 - Prob. 47PECh. 10.2 - Prob. 48PECh. 10.2 - For Exercises 41-50, write the standard form of...Ch. 10.2 - Prob. 50PECh. 10.2 - For Exercises 51-52, a. Determine the eccentricity...Ch. 10.2 - For Exercises 51-52, a. Determine the eccentricity...Ch. 10.2 - Prob. 53PECh. 10.2 - For Exercises 53-54, determine the eccentricity....Ch. 10.2 - Determine the eccentricity of a hyperbola with a...Ch. 10.2 - Prob. 56PECh. 10.2 - Determine the standard form of an equation of a...Ch. 10.2 - Determine the standard form of an equation of a...Ch. 10.2 - Two radio transmitters are 1000 mi apart at points...Ch. 10.2 - Suppose that two microphones 1500m apart at points...Ch. 10.2 - In some designs of eyeglasses, the surface is...Ch. 10.2 - In 1911,Ernest Rutherford discovered the nucleus...Ch. 10.2 - Atomic particles with like charges tend to repel...Ch. 10.2 - A returning boomerang is a V-shaped throwing...Ch. 10.2 - In September 2009, Australian astronomer Robert...Ch. 10.2 - The cross section of a cooling tower of a nuclear...Ch. 10.2 - Prob. 67PECh. 10.2 - Prob. 68PECh. 10.2 - Prob. 69PECh. 10.2 - Prob. 70PECh. 10.2 - For Exercises 71-74, find the standard form of the...Ch. 10.2 - Prob. 72PECh. 10.2 - Prob. 73PECh. 10.2 - For Exercises 71-74, find the standard form of the...Ch. 10.2 - For Exercises 75-76, solve the system of...Ch. 10.2 - For Exercises 75-76, solve the system of...Ch. 10.2 - Given an equation of a hyperbola in standard form,...Ch. 10.2 - Prob. 78PECh. 10.2 - Prob. 79PECh. 10.2 - Prob. 80PECh. 10.2 - A line segment with endpoints on a hyperbola,...Ch. 10.2 - Prob. 82PECh. 10.2 - Prob. 83PECh. 10.2 - a. Radio signals emitted from points 8,0 and 8,0...Ch. 10.2 - Prob. 85PECh. 10.2 - Prob. 86PECh. 10.2 - Prob. 87PECh. 10.2 - For Exercises 85-88, graph the hyperbola from the...Ch. 10.3 - Given a parabola defined by x2=4y , find the focus...Ch. 10.3 - Repeat Example 2 with the equation: x2=8yCh. 10.3 - Prob. 3SPCh. 10.3 - Prob. 4SPCh. 10.3 - Repeat Example 5 with the equation: 4x212x12y+21=0Ch. 10.3 - Prob. 6SPCh. 10.3 - Repeat Example 7 with a radio telescope of...Ch. 10.3 - A is the set of all points in a plane that are...Ch. 10.3 - Prob. 2PECh. 10.3 - The of a parabola is the point of intersection of...Ch. 10.3 - The distance between the vertex and the focus of a...Ch. 10.3 - Given y2=4px with p0, the parabola opens...Ch. 10.3 - Given x2=4py with p0, the parabola opens...Ch. 10.3 - The line segment perpendicular to the axis of...Ch. 10.3 - The length of the latus rectum is called the ...Ch. 10.3 - Given xh2=4pyk , the ordered pairs representing...Ch. 10.3 - Given yk2=4pxh, the ordered pairs representing the...Ch. 10.3 - If the directrix is horizontal, then the parabola...Ch. 10.3 - If the line of symmetry is horizontal, then the...Ch. 10.3 - Prob. 13PECh. 10.3 - For Exercises 13-14, the graph of a parabola is...Ch. 10.3 - For Exercises 15-22, a model of the form x2=4py or...Ch. 10.3 - For Exercises 15-22, a model of the form x2=4py or...Ch. 10.3 - Prob. 17PECh. 10.3 - Prob. 18PECh. 10.3 - Prob. 19PECh. 10.3 - For Exercises 15-22, a model of the form x2=4py or...Ch. 10.3 - For Exercises 15-22, a model of the form x2=4py or...Ch. 10.3 - Prob. 22PECh. 10.3 - A 20-in. satellite dish for a television has...Ch. 10.3 - Solar cookers provide an alternative form of...Ch. 10.3 - If a cross section of the parabolic mirror in a...Ch. 10.3 - A cross section of the parabolic mirror in a car...Ch. 10.3 - For Exercises 27-34, an equation of a parabola...Ch. 10.3 - For Exercises 27-34, an equation of a parabola...Ch. 10.3 - For Exercises 27-34, an equation of a parabola...Ch. 10.3 - For Exercises 27-34, an equation of a parabola...Ch. 10.3 - For Exercises 27-34, an equation of a parabola...Ch. 10.3 - Prob. 32PECh. 10.3 - Prob. 33PECh. 10.3 - For Exercises 27-34, an equation of a parabola...Ch. 10.3 - Prob. 35PECh. 10.3 - For Exercises 35-44, an equation of a parabola...Ch. 10.3 - Prob. 37PECh. 10.3 - For Exercises 35-44, an equation of a parabola...Ch. 10.3 - Prob. 39PECh. 10.3 - For Exercises 35-44, an equation of a parabola...Ch. 10.3 - For Exercises 35-44, an equation of a parabola...Ch. 10.3 - For Exercises 35-44, an equation of a parabola...Ch. 10.3 - For Exercises 35-44, an equation of a parabola...Ch. 10.3 - Prob. 44PECh. 10.3 - Prob. 45PECh. 10.3 - For Exercises 45-52, an equation of a parabola is...Ch. 10.3 - Prob. 47PECh. 10.3 - Prob. 48PECh. 10.3 - For Exercises 45-52, an equation of a parabola is...Ch. 10.3 - For Exercises 45-52, an equation of a parabola is...Ch. 10.3 - For Exercises 45-52, an equation of a parabola is...Ch. 10.3 - For Exercises 45-52, an equation of a parabola is...Ch. 10.3 - Prob. 53PECh. 10.3 - Prob. 54PECh. 10.3 - For Exercises 53-58, fill in the blanks. Let p...Ch. 10.3 - For Exercises 53-58, fill in the blanks. Let p...Ch. 10.3 - For Exercises 53-58, fill in the blanks. Let p...Ch. 10.3 - Prob. 58PECh. 10.3 - If the focal length of a parabola is 6 units and...Ch. 10.3 - Prob. 60PECh. 10.3 - Prob. 61PECh. 10.3 - Prob. 62PECh. 10.3 - For Exercises 61-68, determine the standard form...Ch. 10.3 - Prob. 64PECh. 10.3 - For Exercises 61-68, determine the standard form...Ch. 10.3 - For Exercises 61-68, determine the standard form...Ch. 10.3 - Prob. 67PECh. 10.3 - For Exercises 61-68, determine the standard form...Ch. 10.3 - Suppose that a solar cooker has a parabolic mirror...Ch. 10.3 - A solar water heater is made from a long sheet of...Ch. 10.3 - The Hubble Space Telescope was launched into space...Ch. 10.3 - The James Webb Space Telescope (JWST) is a new...Ch. 10.3 - The Subaru telescope is a large optical-infrared...Ch. 10.3 - A parabolic mirror on a telescope has a focal...Ch. 10.3 - Prob. 75PECh. 10.3 - A cable hanging freely between two vertical...Ch. 10.3 - Prob. 77PECh. 10.3 - For Exercises 77-78, solve the system of nonlinear...Ch. 10.3 - Given an equation of a parabola...Ch. 10.3 - Prob. 80PECh. 10.3 - The surface defined by the equation z=4x2+y2 is...Ch. 10.3 - A jet flies in a parabolic arc to simulate partial...Ch. 10.3 - For Exercises 83-86, graph the parabola from the...Ch. 10.3 - For Exercises 83-86, graph the parabola from the...Ch. 10.3 - For Exercises 83-86, graph the parabola from the...Ch. 10.3 - For Exercises 83-86, graph the parabola from the...Ch. 10.3 - For Exercises 1-8, identify each equation as...Ch. 10.3 - Prob. 2PRECh. 10.3 - Prob. 3PRECh. 10.3 - For Exercises 1-8, identify each equation as...Ch. 10.3 - For Exercises 1-8, identify each equation as...Ch. 10.3 - For Exercises 1-8, identify each equation as...Ch. 10.3 - Prob. 7PRECh. 10.3 - Prob. 8PRECh. 10.3 - For Exercises 9-16, determine whether the equation...Ch. 10.3 - For Exercises 9-16, determine whether the equation...Ch. 10.3 - Prob. 11PRECh. 10.3 - For Exercises 9-16, determine whether the equation...Ch. 10.3 - Prob. 13PRECh. 10.3 - Prob. 14PRECh. 10.3 - Prob. 15PRECh. 10.3 - For Exercises 9-16, determine whether the equation...Ch. 10.3 - For Exercises 17-22, an equation of a degenerate...Ch. 10.3 - Prob. 18PRECh. 10.3 - Prob. 19PRECh. 10.3 - Prob. 20PRECh. 10.3 - Prob. 21PRECh. 10.3 - Prob. 22PRECh. 10.3 - Prob. 23PRECh. 10.3 - Prob. 24PRECh. 10.3 - Given Ax2+Cy2+Dx+Ey+F=0, show that the equation...Ch. 10.4 - Prob. 1SPCh. 10.4 - Suppose that the x- and y-axes are rotated 45...Ch. 10.4 - Write the equation xy=8 in terms of x and y given...Ch. 10.4 - Prob. 4SPCh. 10.4 - Prob. 5SPCh. 10.4 - Prob. 6SPCh. 10.4 - Prob. 1PECh. 10.4 - Prob. 2PECh. 10.4 - Suppose that the equation Ax2+Bxy+Cy2+Dx+Ey+F=0...Ch. 10.4 - The conic section defined by Ax2+Bxy+Cy2+Dx+Ey+F=0...Ch. 10.4 - For Exercises 5-8, the given equation represents a...Ch. 10.4 - For Exercises 5-8, the given equation represents a...Ch. 10.4 - Prob. 7PECh. 10.4 - For Exercises 5-8, the given equation represents a...Ch. 10.4 - Prob. 9PECh. 10.4 - For Exercises 9-14, assume that the x- and y-axes...Ch. 10.4 - Prob. 11PECh. 10.4 - For Exercises 9-14, assume that the x- and y-axes...Ch. 10.4 - Prob. 13PECh. 10.4 - For Exercises 9-14, assume that the x- and y-axes...Ch. 10.4 - Prob. 15PECh. 10.4 - For Exercises 15-18, assume that the x- and y-axes...Ch. 10.4 - Prob. 17PECh. 10.4 - Prob. 18PECh. 10.4 - Prob. 19PECh. 10.4 - Prob. 20PECh. 10.4 - For Exercises 19-22, assume that 02 . Find the...Ch. 10.4 - Prob. 22PECh. 10.4 - For Exercises 23-28, a. Determine an acute angle...Ch. 10.4 - Prob. 24PECh. 10.4 - For Exercises 23-28, a. Determine an acute angle...Ch. 10.4 - For Exercises 23-28, a. Determine an acute angle...Ch. 10.4 - For Exercises 23-28, a. Determine an acute angle...Ch. 10.4 - For Exercises 23-28, a. Determine an acute angle...Ch. 10.4 - Prob. 29PECh. 10.4 - Prob. 30PECh. 10.4 - For Exercises 31-34, the given equation represents...Ch. 10.4 - Prob. 32PECh. 10.4 - Prob. 33PECh. 10.4 - Prob. 34PECh. 10.4 - For Exercises 35-42, the equation represents a...Ch. 10.4 - For Exercises 35-42, the equation represents a...Ch. 10.4 - For Exercises 35-42, the equation represents a...Ch. 10.4 - For Exercises 35-42, the equation represents a...Ch. 10.4 - For Exercises 35-42, the equation represents a...Ch. 10.4 - For Exercises 35-42, the equation represents a...Ch. 10.4 - For Exercises 35-42, the equation represents a...Ch. 10.4 - For Exercises 35-42, the equation represents a...Ch. 10.4 - Prob. 43PECh. 10.4 - Prob. 44PECh. 10.4 - Prob. 45PECh. 10.4 - Prob. 46PECh. 10.4 - Prob. 47PECh. 10.4 - Prob. 48PECh. 10.4 - Given y=33x a. What angle does the line y=33x make...Ch. 10.4 - Given y=22x a. What angle does the line y=22x make...Ch. 10.4 - Prob. 51PECh. 10.4 - Prob. 52PECh. 10.4 - Discuss the graph of x22xy+y21=0.Ch. 10.4 - Discuss the graph of x28xy+y2=0.Ch. 10.4 - Prob. 55PECh. 10.4 - Prob. 56PECh. 10.4 - Prob. 57PECh. 10.4 - Given an equation in x and y, many graphing...Ch. 10.4 - Use the relationships between A,B,andC and...Ch. 10.4 - Prob. 60PECh. 10.4 - For a positive real number r, explain why the...Ch. 10.4 - Show that.x2+y2=r2 is invariant under rotation.Ch. 10.4 - Recall from Section 9.3 that a point Px,y can be...Ch. 10.4 - The set of pointsx1,y1,x2,y2,xn,yn can be...Ch. 10.5 - Graph the equation. r=822cosCh. 10.5 - Prob. 2SPCh. 10.5 - Graph the equation. r=1653cosCh. 10.5 - Rotate the ellipse r=1653cos and graph the result...Ch. 10.5 - Prob. 1PECh. 10.5 - Prob. 2PECh. 10.5 - Prob. 3PECh. 10.5 - Prob. 4PECh. 10.5 - For Exercises 5-10, a. Determine the value of e...Ch. 10.5 - For Exercises 5-10, a. Determine the value of e...Ch. 10.5 - For Exercises 5-10, a. Determine the value of e...Ch. 10.5 - Prob. 8PECh. 10.5 - Prob. 9PECh. 10.5 - Prob. 10PECh. 10.5 - Prob. 11PECh. 10.5 - Prob. 12PECh. 10.5 - For Exercises 11-22, graph the conic. (See...Ch. 10.5 - Prob. 14PECh. 10.5 - Prob. 15PECh. 10.5 - Prob. 16PECh. 10.5 - Prob. 17PECh. 10.5 - Prob. 18PECh. 10.5 - Prob. 19PECh. 10.5 - Prob. 20PECh. 10.5 - Prob. 21PECh. 10.5 - Prob. 22PECh. 10.5 - Prob. 23PECh. 10.5 - For Exercises 23-24, refer to the polar equation...Ch. 10.5 - Prob. 25PECh. 10.5 - For Exercises 25-26, refer to the polar equation...Ch. 10.5 - For Exercises 27-30, write an equation of the...Ch. 10.5 - For Exercises 27-30, write an equation of the...Ch. 10.5 - For Exercises 27-30, write an equation of the...Ch. 10.5 - For Exercises 27-30, write an equation of the...Ch. 10.5 - a. Write a polar equation to represent the...Ch. 10.5 - a. Write a polar equation to represent the...Ch. 10.5 - For Exercises 33-36, convert the equation to...Ch. 10.5 - For Exercises 33-36, convert the equation to...Ch. 10.5 - Prob. 35PECh. 10.5 - Prob. 36PECh. 10.5 - Prob. 37PECh. 10.5 - Prob. 38PECh. 10.5 - Prob. 39PECh. 10.5 - Prob. 40PECh. 10.5 - Prob. 41PECh. 10.5 - Discuss the difference between the graphs of...Ch. 10.5 - Prob. 43PECh. 10.5 - Prob. 44PECh. 10.5 - For Exercises 45-46, use the results of Exercises...Ch. 10.5 - For Exercises 45-46, use the results of Exercises...Ch. 10.5 - Graph the equations r1=210.6cos and r2=210.6cos on...Ch. 10.5 - Prob. 48PECh. 10.5 - Graph the equations r=11esin for e=0.8,1,and1.2 on...Ch. 10.6 - Prob. 1SPCh. 10.6 - Repeat Example 2 with the equations x=t1 and y=t1...Ch. 10.6 - Repeat Example 3 with the equations x=4cos and...Ch. 10.6 - Write parametric equations for the curve defined...Ch. 10.6 - Repeat Example 5 with an ant that begins at A72,10...Ch. 10.6 - Repeat Example 6 with a cannon ball launched from...Ch. 10.6 - If f and g are continuous functions of t over an...Ch. 10.6 - Prob. 2PECh. 10.6 - Identify the endpoints of the curve defined by...Ch. 10.6 - Suppose that an object travels along a straight...Ch. 10.6 - Prob. 5PECh. 10.6 - Prob. 6PECh. 10.6 - For Exercises 7-10, sketch the plane curve by...Ch. 10.6 - For Exercises 7-10, sketch the plane curve by...Ch. 10.6 - Prob. 9PECh. 10.6 - For Exercises 7-10, sketch the plane curve by...Ch. 10.6 - For Exercises 11-26, a. Eliminate the parameter...Ch. 10.6 - For Exercises 11-26, a. Eliminate the parameter...Ch. 10.6 - For Exercises 11-26, a. Eliminate the parameter...Ch. 10.6 - For Exercises 11-26, a. Eliminate the parameter...Ch. 10.6 - Prob. 15PECh. 10.6 - For Exercises 11-26, a. Eliminate the parameter...Ch. 10.6 - Prob. 17PECh. 10.6 - For Exercises 11-26, a. Eliminate the parameter...Ch. 10.6 - Prob. 19PECh. 10.6 - For Exercises 11-26, a. Eliminate the parameter...Ch. 10.6 - Prob. 21PECh. 10.6 - Prob. 22PECh. 10.6 - Prob. 23PECh. 10.6 - Prob. 24PECh. 10.6 - Prob. 25PECh. 10.6 - Prob. 26PECh. 10.6 - Prob. 27PECh. 10.6 - Prob. 28PECh. 10.6 - Prob. 29PECh. 10.6 - For Exercises 27-30, eliminate the parameter and...Ch. 10.6 - Prob. 31PECh. 10.6 - For Exercises 31-34, write parametric equations...Ch. 10.6 - Prob. 33PECh. 10.6 - For Exercises 31-34, write parametric equations...Ch. 10.6 - Prob. 35PECh. 10.6 - Prob. 36PECh. 10.6 - For Exercises 35-42, use the results of Exercises...Ch. 10.6 - Prob. 38PECh. 10.6 - For Exercises 35-42, use the results of Exercises...Ch. 10.6 - For Exercises 35-42, use the results of Exercises...Ch. 10.6 - For Exercises 35-42, use the results of Exercises...Ch. 10.6 - For Exercises 35-42, use the results of Exercises...Ch. 10.6 - For Exercises 43-46, write parametric equations on...Ch. 10.6 - For Exercises 43-46, write parametric equations on...Ch. 10.6 - For Exercises 43-46, write parametric equations on...Ch. 10.6 - For Exercises 43-46, write parametric equations on...Ch. 10.6 - For Exercises 47-48, an object undergoes uniform...Ch. 10.6 - Prob. 48PECh. 10.6 - Prob. 49PECh. 10.6 - A hospital is located 3mi west and 4mi north of...Ch. 10.6 - Prob. 51PECh. 10.6 - A golfer tees off on level ground, and hits the...Ch. 10.6 - Anna hits a softball at a height of 3ft from the...Ch. 10.6 - Tony hits a baseball at a height of 3ft from the...Ch. 10.6 - Prob. 55PECh. 10.6 - Two planes flying at the same altitude are on a...Ch. 10.6 - Suppose that a mortar is fired from ground level...Ch. 10.6 - Prob. 58PECh. 10.6 - Prob. 59PECh. 10.6 - Prob. 60PECh. 10.6 - Prob. 61PECh. 10.6 - For Exercises 61-62, describe the differences in...Ch. 10.6 - Do the parametric equations x=t and y=t+5 define a...Ch. 10.6 - Is the point 16,12 on the curve defined by x=2t...Ch. 10.6 - For a short interval of time, a military supply...Ch. 10.6 - Prob. 66PECh. 10.6 - Suppose that an imaginary string of unlimited...Ch. 10.6 - For Exercises 68-70, use a graphing utility to...Ch. 10.6 - Prob. 69PECh. 10.6 - Prob. 70PECh. 10.6 - A cycloid is a curve created by rolling a circle...Ch. 10.6 - A cycloid is a curve created by rolling a circle...Ch. 10.6 - If a circle of radius r rolls around the exterior...Ch. 10.6 - If a circle of radius r rolls around the exterior...Ch. 10 - How are the graphs of these ellipses similar and...Ch. 10 - For Exercises 2-5, an equation of an ellipse is...Ch. 10 - For Exercises 2-5, an equation of an ellipse is...Ch. 10 - For Exercises 2-5, an equation of an ellipse is...Ch. 10 - For Exercises 2-5, an equation of an ellipse is...Ch. 10 - For Exercises 6-7, a. Write the equation of the...Ch. 10 - For Exercises 6-7, a. Write the equation of the...Ch. 10 - For Exercises 8-10, write the standard form of an...Ch. 10 - Prob. 9RECh. 10 - For Exercises 8-10, write the standard form of an...Ch. 10 - Jupiter orbits the Sun in an elliptical path with...Ch. 10 - A bridge over a gorge is supported by an arch in...Ch. 10 - Prob. 14RECh. 10 - For Exercises 15-16, an equation of a hyperbola is...Ch. 10 - For Exercises 15-16, an equation of a hyperbola is...Ch. 10 - For Exercises 17-20, an equation of a hyperbola is...Ch. 10 - For Exercises 17-20, an equation of a hyperbola is...Ch. 10 - For Exercises 17-20, an equation of a hyperbola is...Ch. 10 - For Exercises 17-20, an equation of a hyperbola is...Ch. 10 - For Exercises 21-22, a. Write the equation of the...Ch. 10 - For Exercises 21-22, a. Write the equation of the...Ch. 10 - For Exercises 23-25, write the standard form of an...Ch. 10 - For Exercises 23-25, write the standard form of an...Ch. 10 - For Exercises 23-25, write the standard form of an...Ch. 10 - Suppose that one hyperbola has an eccentricity of...Ch. 10 - Solve the system of equations. 6x22y2=122x2+y2=11Ch. 10 - Suppose that two people standing 2mi10,560ft apart...Ch. 10 - A 120-ft flight control tower in the shape of a...Ch. 10 - For Exercises 30-33, an equation of a parabola is...Ch. 10 - For Exercises 30-33, an equation of a parabola is...Ch. 10 - For Exercises 30-33, an equation of a parabola is...Ch. 10 - Prob. 33RECh. 10 - Prob. 34RECh. 10 - For Exercises 34-35, an equation of a parabola is...Ch. 10 - For Exercises 36-37, fill in the blank. Let p...Ch. 10 - For Exercises 36-37, fill in the blank. Let p...Ch. 10 - For Exercises 38-40, determine the standard form...Ch. 10 - For Exercises 38-40, determine the standard form...Ch. 10 - Prob. 40RECh. 10 - Solve the system of equations. y+22=3x5xy=7Ch. 10 - Prob. 42RECh. 10 - Two large airship hangars were built in Orly,...Ch. 10 - Prob. 44RECh. 10 - For Exercises 44-45, the given equation represents...Ch. 10 - Prob. 46RECh. 10 - Prob. 47RECh. 10 - For Exercises 46-48, assume that the x- and y-axes...Ch. 10 - For Exercises 49-51, an equation of a conic...Ch. 10 - Prob. 50RECh. 10 - Prob. 51RECh. 10 - For Exercises 52-53, the equation represents a...Ch. 10 - Prob. 53RECh. 10 - Prob. 54RECh. 10 - Prob. 55RECh. 10 - For Exercises 54-59, a. Identify the type of conic...Ch. 10 - For Exercises 54-59, a. Identify the type of conic...Ch. 10 - Prob. 58RECh. 10 - Prob. 59RECh. 10 - Prob. 60RECh. 10 - Prob. 61RECh. 10 - Prob. 62RECh. 10 - Prob. 63RECh. 10 - Prob. 64RECh. 10 - x=4t2 and y=2t for 2t2 Sketch the plane curve by...Ch. 10 - Prob. 66RECh. 10 - Prob. 67RECh. 10 - Prob. 68RECh. 10 - Prob. 69RECh. 10 - Prob. 70RECh. 10 - For each given curve, the parameter t represents...Ch. 10 - Prob. 72RECh. 10 - Suppose that the origin on a computer screen is at...Ch. 10 - A stunt man drives a car at a speed of 25m/sec off...Ch. 10 - Suppose that a baseball is thrown at an angle of...Ch. 10 - How are the graphs of these ellipses similar, and...Ch. 10 - Prob. 2TCh. 10 - Write the standard form of an equation of an...Ch. 10 - Prob. 4TCh. 10 - Prob. 5TCh. 10 - Prob. 6TCh. 10 - Write the standard form of an equation of a...Ch. 10 - Write the standard form of an equation of a...Ch. 10 - For Exercises 9-16, a. Identify the equation as...Ch. 10 - For Exercises 9-16, a. Identify the equation as...Ch. 10 - For Exercises 9-16, a. Identify the equation as...Ch. 10 - For Exercises 9-16, a. Identify the equation as...Ch. 10 - For Exercises 9-16, a. Identify the equation as...Ch. 10 - For Exercises 9-16, a. Identify the equation as...Ch. 10 - Prob. 15TCh. 10 - For Exercises 9-16, a. Identify the equation as...Ch. 10 - The entrance to a tunnel is in the shape of a...Ch. 10 - Prob. 18TCh. 10 - Suppose that two people standing 1.5mi7920ft apart...Ch. 10 - Prob. 20TCh. 10 - Prob. 21TCh. 10 - Prob. 22TCh. 10 - Write the standard form of an equation of an...Ch. 10 - Write the standard form of an equation of a...Ch. 10 - Prob. 25TCh. 10 - If the major axis of an ellipse is 26 units in...Ch. 10 - Prob. 27TCh. 10 - Prob. 28TCh. 10 - If the asymptotes of a hyperbola are y=35x+1 and...Ch. 10 - Solve the system of equations. 3x24y2=135x2+2y2=13Ch. 10 - Describe the graph of the equation. x=41y29Ch. 10 - Prob. 32TCh. 10 - Prob. 33TCh. 10 - Prob. 34TCh. 10 - Prob. 35TCh. 10 - For Exercises 36-37, an equation of a conic...Ch. 10 - Prob. 37TCh. 10 - Prob. 38TCh. 10 - Prob. 39TCh. 10 - Prob. 40TCh. 10 - For Exercises 41-42, a. Eliminate the parameter....Ch. 10 - For Exercises 41-42, a. Eliminate the parameter....Ch. 10 - Prob. 43TCh. 10 - A pyrotechnic rocket is fired from a platform 2ft...Ch. 10 - Prob. 45TCh. 10 - Prob. 46TCh. 10 - Use the parametric mode to graph the curve on a...Ch. 10 - Prob. 1CRECh. 10 - Is 4 a zero of the polynomial fx=3x46x3+5x12?Ch. 10 - Prob. 3CRECh. 10 - Prob. 4CRECh. 10 - For Exercises 4-5, simplify completely....Ch. 10 - Find the midpoint of the line segment with...Ch. 10 - Given fx=x73, write an equation defining f1x.Ch. 10 - Prob. 8CRECh. 10 - Determine the asymptotes of the graph of y=csc2x2Ch. 10 - For Exercises 10-15, solve the equation or...Ch. 10 - For Exercises 10-15, solve the equation or...Ch. 10 - For Exercises 10-15, solve the equation or...Ch. 10 - Prob. 13CRECh. 10 - For Exercises 10-15, solve the equation or...Ch. 10 - For Exercises 10-15, solve the equation or...Ch. 10 - Prob. 16CRECh. 10 - Graph y=2sinx4 over one completed period.Ch. 10 - Prob. 18CRECh. 10 - Prob. 19CRECh. 10 - Prob. 20CRECh. 10 - Prob. 21CRECh. 10 - Prob. 22CRECh. 10 - For Exercises 21-24, graph the equations and...Ch. 10 - For Exercises 21-24, graph the equations and...Ch. 10 - For Exercises 25-26, solve the system....Ch. 10 - For Exercises 25-26, solve the system....Ch. 10 - For Exercises 27-29, refer to the matrices A and B...Ch. 10 - For Exercises 27-29, refer to the matrices A and B...Ch. 10 - For Exercises 27-29, refer to the matrices A and B...Ch. 10 - Use Cramer's rule to solve for z ....

Additional Math Textbook Solutions

Find more solutions based on key concepts
A categorical variable has three categories, with the following frequencies of occurrence: a. Compute the perce...

Basic Business Statistics, Student Value Edition

Find the counterclockwise circulation and outward flux of the field around and over the boundary of the region...

University Calculus: Early Transcendentals (4th Edition)

Calculate percent as a fraction for each continent.   

Pre-Algebra Student Edition

A pair of fair dice is rolled. What is the probability that the second die lands on a higher value than does th...

A First Course in Probability (10th Edition)

Women’s Heights Suppose college women’s heights are approximately Normally distributed with a mean of 65 inches...

Introductory Statistics

Calculating derivatives Find dy/dx for the following functions. 23. y=cosxsinx+1

Calculus: Early Transcendentals (2nd Edition)

Knowledge Booster
Background pattern image
Calculus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Text book image
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
Text book image
Algebra for College Students
Algebra
ISBN:9781285195780
Author:Jerome E. Kaufmann, Karen L. Schwitters
Publisher:Cengage Learning
Text book image
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Text book image
College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Text book image
College Algebra
Algebra
ISBN:9781337282291
Author:Ron Larson
Publisher:Cengage Learning
SEE MORE TEXTBOOKS
08 - Conic Sections - Hyperbolas, Part 1 (Graphing, Asymptotes, Hyperbola Equation, Focus); Author: Math and Science;https://www.youtube.com/watch?v=Ryj0DcdGPXo;License: Standard YouTube License, CC-BY