Chapter 10.1, Problem 99PE

This exercise guides you through the steps to find the standard form of an equation of an ellipse centered at the origin with foci on the $x\text{-axis}\text{.}$

a. Refer to the figure to verify that the distance from $F_1\text{ to }{V}_2\text{ is }\left(a+c\right)$ and the distance from $F_2\text{ to }{V}_2\text{ is }\left(a-c\right).$ is Verify that the sum of these distances is $2a.$

b. Write an expression that represents the sum of the distances from $F_1$ to $\left(x,y\right)$ and from $F_2$ to $\left(x,y\right).$ Then set this expression equal to $2a.$

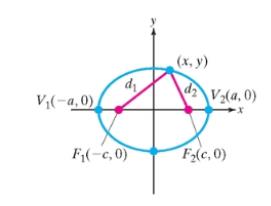
c. Given the equation $\sqrt{{\left(x+c\right)}^2+y^2}+\sqrt{{\left(x-c\right)}^2+y^2}=2a,$ isolate the leftmost radical and square both sides of the equation. Show that the equation can be written as $a\sqrt{{\left(x-c\right)}^2+y^2}=a^2-xc.$

d. Square both sides of the equation $a\sqrt{{\left(x-c\right)}^2+y^2}=a^2-xc$ and show that the equation can be written as $\left(a^2-c^2\right)x^2+a^2{y}^2=a^2\left(a^2-c^2\right).$ (Hint. Collect variable terms on the left side of the equation and constant terms on the right side.)

e. Replace $a^2-c^2$ by $b^2.$ Then divide both sides of the equation by $a^2{b}^2.$ Verify that the resulting equation is $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1.$