
A spring of constant 15 kN/m connects points C and F of the linkage shown. Neglecting the weight of the spring and linkage, determine the force in the spring and the vertical motion of point G when a vertical downward 120-N force is applied (a) at point E, (b) at points E and F.
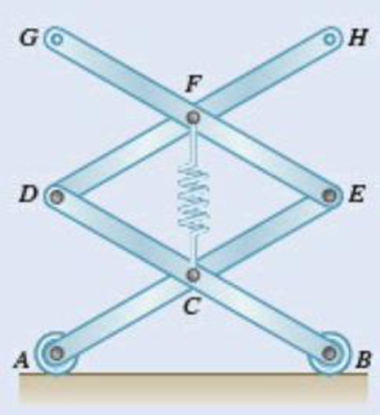
Fig. P10.5 and P10.6
(a)
Find the force in the spring and the vertical motion of point G when a vertical load of
Answer to Problem 10.6P
The force in the spring is
The vertical motion of point G is
Explanation of Solution
Given information:
The spring constant is
Calculation:
Show the free-body diagram of the spring assembly as in Figure 1.
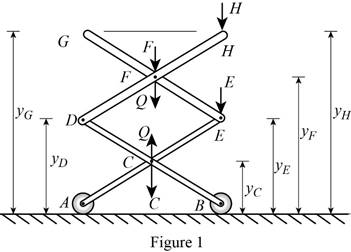
Write the relation of the deflections at point G, H, F, E, D with C as follows;
The deflection
Assume the spring force Q is in tension.
Find the force in the spring Q using the relation.
Here, the spring constant is k.
Substitute
Use the virtual work principle:
Here,
Substitute 0 for C,
The spring force Q is in compression. The assumption is incorrect.
Therefore, the force in the spring is
Substitute –120 N for Q in Equation (1).
Find the vertical motion
Substitute –4 mm for
Therefore, the vertical motion of point G is
(b)
Find the force in the spring and the vertical motion of point G when a vertical load of 120-N force is applied at point E and F.
Answer to Problem 10.6P
The force in the spring is
The vertical motion of point G is
Explanation of Solution
Given information:
The spring constant is
Calculation:
Use the virtual work principle:
Here,
Substitute 0 for C,
The spring force Q is in compression. The assumption is incorrect.
Therefore, the force in the spring is
Substitute –300 N for Q in Equation (1).
Find the vertical motion
Substitute –10 mm for
Therefore, the vertical motion of point G is
Want to see more full solutions like this?
Chapter 10 Solutions
EBK VECTOR MECHANICS FOR ENGINEERS: STA
- A 4 ft 300 Ib 1000 Ib.ft 350 Ib C 2 ft 3. 45° 250 Ib B. 3ft B 25ft 200 Ib 150 Ib Replace the force system acting on the frame shown in the figure by a resultant force (magnitude and direction), and specify where its line of action intersects member (AB), measured from point (A).arrow_forwardCan you research the standard percentage of Steam Quality in:(1.) Boiler - leaving boilerBoiler -> Out(2.) Condenser - coming in condenser In -> CondenserProvide reference Also define: steam quality, its purpose and importancearrow_forwardNumbers 1 and 2 and 5 are are optional problems. However, I only need the values (with units) of 3, 4 and 6. Thank you :)arrow_forward
- Three cables are pulling on a ring located at the origin, as shown in the diagram below. FA is 200 N in magnitude with a transverse angle of 30° and an azimuth angle of 140°. FB is 240 N in magnitude with coordinate direction angles α = 135° and β = 45°. Determine the magnitude and direction of FC so that the resultant of all 3 force vectors lies on the z-axis and has a magnitude of 300 N. Specify the direction of FC using its coordinate direction angles.arrow_forwardturbomachieneryarrow_forwardauto controlsarrow_forward
- auto controlsarrow_forward1 Pleasearrow_forwardA spring cylinder system measures the pressure. Determine which spring can measure pressure between 0-1 MPa with a large excursion. The plate has a diameter of 20 mm. Also determine the displacement of each 0.1 MPa step.Spring power F=c x fF=Springpower(N)c=Spring constant (N/mm)f=Suspension (mm) How do I come up with right answer?arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





