Videos
a)
To determine: The probability of earning more than 10 percent on long-term corporate bonds.
Introduction:
The
Standard deviation refers to the variation in the actual observations from the average.
Z-Score helps to know how many numbers of standard deviations is the raw score or outcome away from the average or mean.
a)
Answer to Problem 28QP
The probability of earning more than 10 percent on long-term corporate bonds is 33.41 percent.
Explanation of Solution
Given information:
Assume that the returns of long-term corporate bonds have a normal distribution. The average return or mean of long-term corporate bonds is 6.4 percent, and the standard deviation is 8.4 percent (Refer to Figure 10.10 in the text).
Determine the probability of having a return greater than 10 percent on long-term government bonds:
Follow the common steps from Step 1 to Step 3 given below. Then, proceed with the Step 4.
The common steps to be followed to use the “NORM.DIST” function in Excel:
Step 1:
Open an Excel worksheet.
Step 2:
Place the cursor in cell A1.
Step 3:
Select the “Formulas” tab, and go to “More functions” in the ribbon. Under “More functions”, select “Statistical”. Under the drop-down menu of “Statistical”, select “NORM.DIST” function.
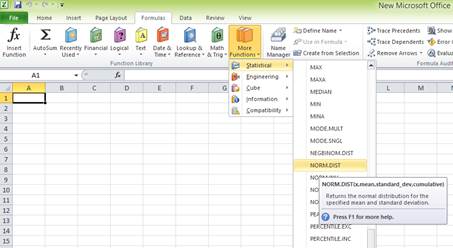
After clicking the “NORM.DIST” function, a popup window named “Function arguments” appears.
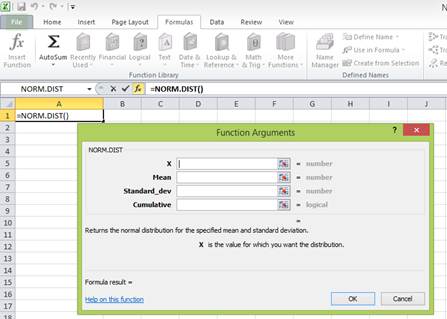
Step 4:
Enter the values. “X” represents the raw score or outcome. Here, it is necessary to test the probability of having more than 10 percent returns. Hence, “X” equals 10 percent. The mean or average return is 6.4 percent. The standard deviation is 8.4 percent. The cumulative distribution function provides the probability of the area to the left of Z. Hence, enter “TRUE” in the “Cumulative” column.
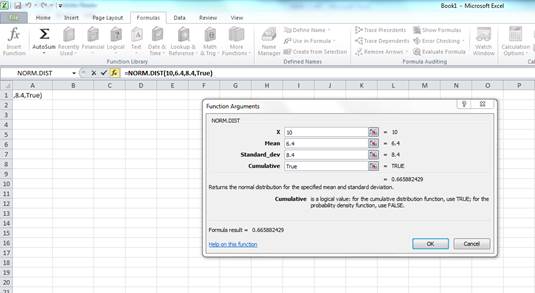
Press “OK” after providing the inputs. The probability of the area to the left of Z is as follows:
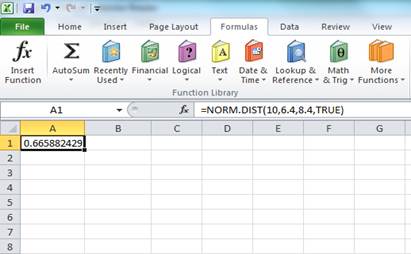
The probability of 0.665882 represents the area to the left of Z. The area to the left of Z is the probability of getting less than 10 percent return. The area to the right of Z is the probability of getting a return of 10 percent or more.
The total area represented by the normal distribution curve has a probability of “1”. The area to the left of Z has a probability of 0.665882. Hence, the probability of the area to the right of Z is “1” minus the probability of the area to the left of Z. Hence, the probability of getting 10 percent return or more is 0.334118 or 33.4118 percent
To determine: The probability of earning less than 0 percent on long-term corporate bonds
Answer to Problem 28QP
The probability of earning less than 0 percent on long-term corporate bonds is 0.223058 or 0.223058 percent
Explanation of Solution
Given information:
Assume that the returns of long-term corporate bonds have a normal distribution. The average return or mean of long-term corporate bonds is 6.4 percent, and the standard deviation is 8.4 percent (Refer to Figure 10.10 in the text).
Determine the probability of having a return less than 0 percent on long-term government bonds:
Follow the common steps from Step 1 to Step 3 given below. Then, proceed with the Step 4.
The common steps to be followed to use the “NORM.DIST” function in Excel:
Step 1:
Open an Excel worksheet.
Step 2:
Place the cursor in cell A1.
Step 3:
Select the “Formulas” tab, and go to “More functions” in the ribbon. Under “More functions”, select “Statistical”. Under the drop-down menu of “Statistical”, select “NORM.DIST” function.
After clicking the “NORM.DIST” function, a popup window named “Function arguments” appears.
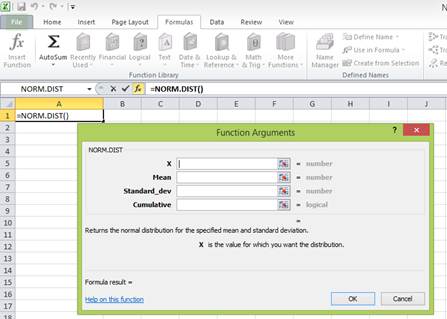
Step 4:
Enter the values. “X” represents the raw score or outcome. Here, it is necessary to test the probability of having (0 percent) return or less. Hence, “X” equals (0 percent). The mean or average return is 6.4 percent. The standard deviation is 8.4 percent. The cumulative distribution function provides the probability of the area to the left of Z. Hence, enter “TRUE” in the “Cumulative” column.
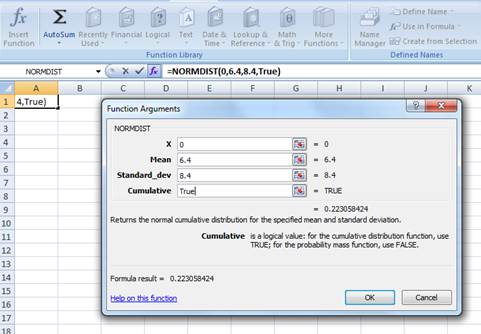
Press “OK” after providing the inputs. The probability of the area to the left of Z is as follows:
The probability of 0.223058 represents the area to the left of Z. The area to the left of Z refers to the probability of getting (0 percent) return or less because the left-hand side of the normal distribution curve indicates negative returns. Hence, the probability of earning less than 0 percent is 0.223058 or 0.223058 percent.
b)
To determine: The probability of earning more than 10 percent on Treasury bills
b)
Answer to Problem 28QP
The probability of earning more than 10 percent on Treasury bills is 0.018006785 or 1.80 percent.
Explanation of Solution
Given information:
Assume that the returns of Treasury bills have a normal distribution. The average return or mean of Treasury bills is 3.5 percent, and the standard deviation is 3.1 percent (Refer to Figure 10.10 in the textbook).
Determine the probability of having a return greater than 10 percent on Treasury bills:
Follow the common steps from Step 1 to Step 3 given below. Then, proceed with the Step 4.
The common steps to be followed to use the “NORM.DIST” function in Excel:
Step 1:
Open an Excel worksheet.
Step 2:
Place the cursor in cell A1.
Step 3:
Select the “Formulas” tab, and go to “More functions” in the ribbon. Under “More functions”, select “Statistical”. Under the drop-down menu of “Statistical”, select “NORM.DIST” function.
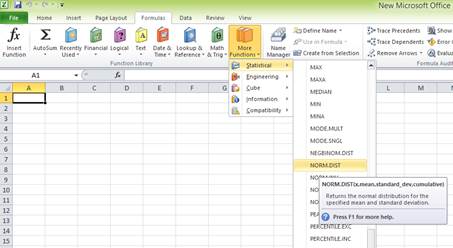
After clicking the “NORM.DIST” function, a popup window named “Function arguments” appears.
Step 4:
Enter the values. “X” represents the raw score or outcome. Here, it is necessary to test the probability of having more than 10 percent returns. Hence, “X” equals 10 percent. The mean or average return is 3.5 percent. The standard deviation is 3.1 percent. The cumulative distribution function provides the probability of the area to the left of Z. Hence, enter “TRUE” in the “Cumulative” column.
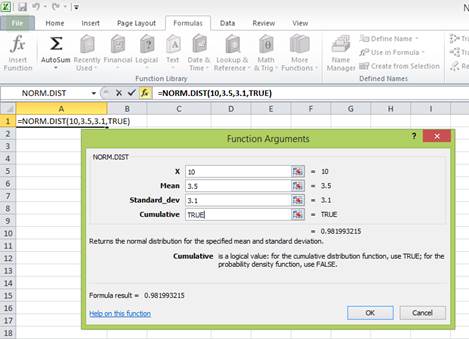
Press “OK” after providing the inputs. The probability of the area to the left of Z is as follows:
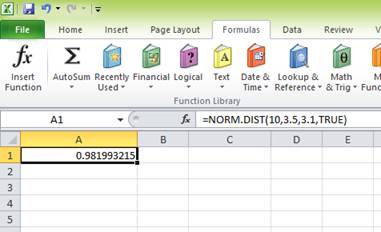
The probability of 0.981993215 represents the area to the left of Z. The area to the left of Z is the probability of getting less than 10 percent return. The area to the right of Z is the probability of getting a return of 10 percent or more.
The total area represented by the normal distribution curve has a probability of “1”. The area to the left of Z has a probability of 0.981993215. Hence, the probability of the area to the right of Z is “1” minus the probability of the area to the left of Z. Hence, the probability of getting 10 percent return or more is 0.018006785 or 1.80 percent
To determine: The probability of earning less than 0 percent on Treasury bills.
Answer to Problem 28QP
The probability of earning less than 0 percent on Treasury bills is 0.129442113 or 12.94 percent.
Explanation of Solution
Given information:
Assume that the returns of Treasury bills have a normal distribution. The average return or mean of Treasury bills is 3.5 percent, and the standard deviation is 3.1 percent (Refer to Figure 10.10 in the text).
Determine the probability of having a return less than 0 percent on Treasury bills:
Follow the common steps from Step 1 to Step 3 given below. Then, proceed with the Step 4.
The common steps to be followed to use the “NORM.DIST” function in Excel:
Step 1:
Open an Excel worksheet.
Step 2:
Place the cursor in cell A1.
Step 3:
Select the “Formulas” tab, and go to “More functions” in the ribbon. Under “More functions”, select “Statistical”. Under the drop-down menu of “Statistical”, select “NORM.DIST” function.
After clicking the “NORM.DIST” function, a popup window named “Function arguments” appears.
Step 4:
Enter the values. “X” represents the raw score or outcome. Here, it is necessary to test the probability of having (0 percent) return or less. Hence, “X” equals (0 percent). The mean or average return is 3.5 percent. The standard deviation is 3.1 percent. The cumulative distribution function provides the probability of the area to the left of Z. Hence, enter “TRUE” in the “Cumulative” column.
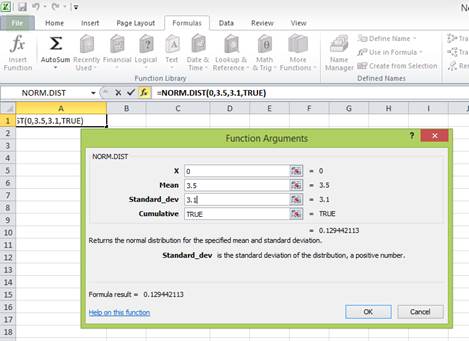
Press “OK” after providing the inputs. The probability of the area to the left of Z is as follows:
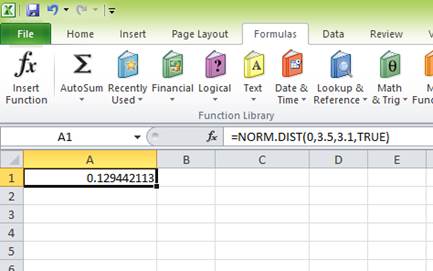
The probability of 0.129442113 represents the area to the left of Z. The area to the left of Z refers to the probability of getting (0 percent) return or less because the left-hand side of the normal distribution curve indicates negative returns. Hence, the probability of earning less than 0 percent is 0.129442113 or 12.94 percent.
c)
To determine: The probability of earning (4.18 percent) on long-term corporate bonds.
c)
Answer to Problem 28QP
The probability of earning (4.18 percent) on long-term corporate bonds is 0.1039 or 10.39 percent.
Explanation of Solution
Given information:
Assume that the returns of long-term corporate bonds have a normal distribution. The average return or mean of long-term corporate bonds is 6.4 percent, and the standard deviation is 8.4 percent (Refer to Figure 10.10 in the textbook).
Determine the probability of having (4.18 percent) on long-term government bonds:
Follow the common steps from Step 1 to Step 3 given below. Then, proceed with the Step 4.
The common steps to be followed to use the “NORM.DIST” function in Excel:
Step 1:
Open an Excel worksheet.
Step 2:
Place the cursor in cell A1.
Step 3:
Select the “Formulas” tab, and go to “More functions” in the ribbon. Under “More functions”, select “Statistical”. Under the drop-down menu of “Statistical”, select “NORM.DIST” function.
After clicking the “NORM.DIST” function, a popup window named “Function arguments” appears.
Step 4:
Enter the values. “X” represents the raw score or outcome. Here, it is necessary to test the probability of having (4.18 percent) return or less. Hence, “X” equals (4.18 percent). The mean or average return is 6.4 percent. The standard deviation is 8.4 percent. The cumulative distribution function provides the probability of the area to the left of Z. Hence, enter “TRUE” in the “Cumulative” column.
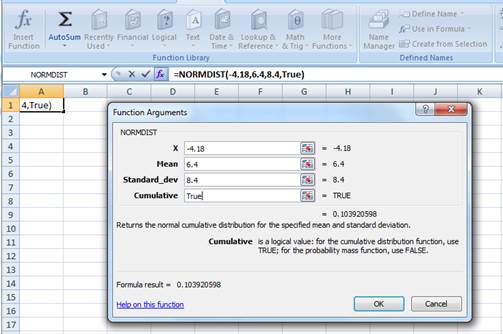
Press “OK” after providing the inputs. The probability of the area to the left of Z is as follows:
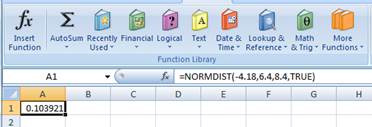
The probability of 0.103921 represents the area to the left of Z. The area to the left of Z refers to the probability of getting (4.18 percent) return or less because the left-hand side of the normal distribution curve indicates negative returns. Hence, the probability of earning (4.18 percent) is 0.1039 or 10.39 percent.
To determine: The probability of earning 10.56 percent on Treasury bills.
Answer to Problem 28QP
The probability of earning 10.56 percent on Treasury bills is 0.011380598 or 1.14 percent
Explanation of Solution
Given information:
Assume that the returns of Treasury bills have a normal distribution. The average return or mean of Treasury bills is 3.5 percent, and the standard deviation is 3.1 percent (Refer to Figure 10.10 in the text).
Determine the probability of having a return of 10.56 percent on Treasury bills:
Follow the common steps from Step 1 to Step 3 given below. Then, proceed with the Step 4.
The common steps to be followed to use the “NORM.DIST” function in Excel:
Step 1:
Open an Excel worksheet.
Step 2:
Place the cursor in cell A1.
Step 3:
Select the “Formulas” tab, and go to “More functions” in the ribbon. Under “More functions”, select “Statistical”. Under the drop-down menu of “Statistical”, select “NORM.DIST” function.
After clicking the “NORM.DIST” function, a popup window named “Function arguments” appears.
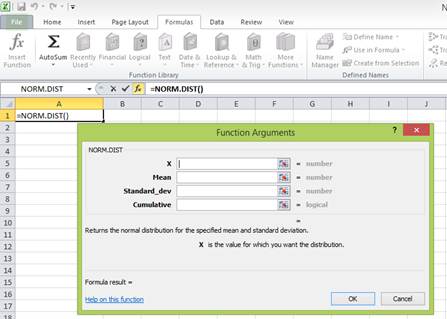
Step 4:
Enter the values. “X” represents the raw score or outcome. Here, it is necessary to test the probability of having 10.56 percent returns. Hence, “X” equals 10.56 percent. The mean or average return is 3.5 percent. The standard deviation is 3.1 percent. The cumulative distribution function provides the probability of the area to the left of Z. Hence, enter “TRUE” in the “Cumulative” column.
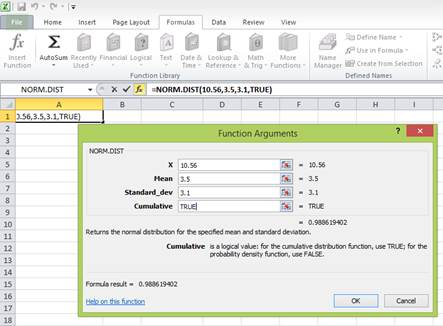
Press “OK” after providing the inputs. The probability of the area to the left of Z is as follows:
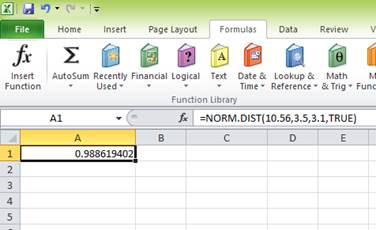
The probability of 0.988619402 represents the area to the left of Z. The area to the left of Z is the probability of getting less than 10.56 percent return. The area to the right of Z is the probability of getting a return of 10.56 percent or more.
The total area represented by the normal distribution curve has a probability of “1”. The area to the left of Z has a probability of 0.988619402. Hence, the probability of the area to the right of Z is “1” minus the probability of the area to the left of Z. Hence, the probability of getting 10.56 percent return or more is 0.011380598 or 1.14 percent
Want to see more full solutions like this?
Chapter 10 Solutions
Essentials of Corporate Finance (Mcgraw-hill/Irwin Series in Finance, Insurance, and Real Estate)
- Could you help to explain: How researchers can demonstrate Biblical ethics when conducting a literature review? How researchers can demonstrate Biblical ethics when communicating with a research team or university committee? How researchers can demonstrate Biblical ethics when recruiting participants. Provide Biblical and/or scholarly support for all assertions?arrow_forwardCould you please help explain what is the Biblical ethics in research? How do they establish a firm ethical foundation based on Biblical principles? What should they do to reduce the researcher bias as well as misrepresenting the literature and study findings? How Christians would like to ensure of being obedient to God in the research and study conduct?arrow_forwardI need answer typing clear urjent no chatgpt used pls i will give 5 Upvotes.arrow_forward
- < When you purchased your car, you took out a 5-year annual-payment loan with an interest rate of 5% per year. The annual payment on the car is $5,200. You have just made a payment and have now decided to pay off the loan by repaying the outstanding balance. What is the payoff amount for the following scenarios? a. You have owned the car for 1 year (so there are 4 years left on the loan)? b. You have owned the car for 4 years (so there is 1 year left on the loan)? a. You have owned the car for 1 year (so there are 4 years left on the loan)? The payoff if there are 4 years left on the loan is $ (Round to the nearest cent.) b. You have owned the car for 4 years (so there is 1 year left on the loan)? The payoff if there is 1 year left on the loan is $ (Round to the nearest cent.)arrow_forwardVictoria Exports (Canada). A Canadian exporter, Victoria Exports, will be receiving six payments of €13,800, ranging from now to 12 months in the future. Since the company keeps cash balances in both Canadian dollars and U.S. dollars, it can choose which currency to exchange the euros for at the end of the various periods. Which currency appears to offer the better rates in the forward market? (Click on the icon to import the table into a spreadsheet.) Period Days Forward spot 1 month C$/euro 1.3347 1.3370 US$/euro 1.3219 1.3224 m 2 months 3 months 1.3392 30 60 1.3229 90 1.3235 180 1.3438 12 months 360 1.3464 1.3239 1.3269 6 months 1.3416 Calculate the forward premium, the Canadian dollar proceeds, and the difference from the spot rate proceeds in the C$/Euro forward market below: (Round the forward premium to three decimal places and the Canadian dollar amounts to the nearest cent.) Days Forward Premium C$ Proceeds of Difference Period Forward C$/euro on the C$/euro €13,800 Over Spot…arrow_forwardidentify the primary sources of financing, both traditional and alternative, accessible to companies seeking sources of funding. To do so, you should: Collect and curate data and documentary resources from various sources (magazine articles, newspapers, online content, working papers from various institutions, activity reports, performance reports, legal regulations, speeches, appearances, press conferences, etc.). Analyze the documentary content you have previously curated and collected. During your analysis, consider the context, location, timing, and target audience of the texts. Reference Article: One Park Financial. (2022). Best alternative business loans and financing for entrepreneurs. https://www.oneparkfinancial.com/blog/alternative-business-funding Questions: Identify and summarize the traditional financial avenues available to businesses. What are the most innovative financing options they could find? Open-ended question: if you were in the opposite position, as an…arrow_forward
- XYZ stock price and dividend history are as follows: Beginning-of- $ 130 Dividend Paid at Year Year Price Year-End 2021 $ 2 2022 2023 153 2 2024 128 133 2 2 An investor buys five shares of XYZ at the beginning of 2021, buys another two shares at the beginning of 2022, sells one share at the beginning of 2023, and sells all six remaining shares at the beginning of 2024. Required: a. What are the arithmetic and geometric average time-weighted rates of return for the investor? Note: Do not round intermediate calculations. Round your answers to 2 decimal places. Arithmetic time-weighted average returns Geometric time-weighted average returns % % b-1. Prepare a chart of cash flows for the four dates corresponding to the turns of the year for January 1, 2021, to January 1, 2024. Note: Negative amounts should be indicated by a minus sign. Date 01/01/2021 01/01/2022 Cash Flow 01/01/2023 01/01/2024 b-2. What is the dollar-weighted rate of return? (Hint. If your calculator cannot calculate…arrow_forwardConsider the following two banks: Bank 1 has assets composed solely of a 10-year, 11.50 percent coupon, $1.5 million loan with a 11.50 percent yield to maturity. It is financed with a 10-year, 10 percent coupon, $1.5 million CD with a 10 percent yield to maturity. Bank 2 has assets composed solely of a 7-year, 11.50 percent, zero-coupon bond with a current value of $1,108,283.85 and a maturity value of $2,374,515.87. It is financed with a 10-year, 5.75 percent coupon, $1,500,000 face value CD with a yield to maturity of 10 percent. All securities except the zero-coupon bond pay interest annually. a. If interest rates rise by 1 percent (100 basis points), what is the difference in the value of the assets and liabilities of each bank? Note: Do not round intermediate calculations. Negative amounts should be indicated by a minus sign. Enter the answers in dollars, not millions of dollars. Round your answers to 2 decimal places. (e.g., 32.16) Before Interest Asset Value After Interest…arrow_forwardTIME TO REACH A FINANCIAL GOAL You have $42,180.53 in a brokerage account, and you plan to deposit an additional $5,000 at the end of every future year until your account totals $250,000. You expect to earn 12% annually on the account. How many years will it take to reach your goal? Round UP to the nearest year. (Example 5.01 years = 6 years) Your answer should include numerical value only.arrow_forward
- You plan to retire in 30 years. • In 50 years, you want to give your daughter a $500,000 gift. • You will receive an inheritance of $200,000 in 25 years. • You think you will want $50,000 per year when you retire for 30 years (the first withdrawal will come one year after retirement). • You will begin saving an amount to meet your retirement goals one year from today. Required: • If you think you can make 9% on your investments, how much will you need to save each year for the next 30 years to meet your retirement goals?arrow_forwardAn initial $3300 investment was worth $3820 after two years and six months. What quarterly compounded nominal rate of return did the investment earn? (Do not round intermediate calculations and round your final answer to 2 decimal places.) Nominal rate of return % compounded quarterly.arrow_forwardSuppose your firm is considering investing in a project with the cash flows shown below, that the required rate of return on projects of this risk class is 9 percent, and that the maximum allowable payback and discounted payback statistics for the project are 2.0 and 3.0 years, respectively.arrow_forward
Intermediate Financial Management (MindTap Course...FinanceISBN:9781337395083Author:Eugene F. Brigham, Phillip R. DavesPublisher:Cengage Learning
