
Concept explainers
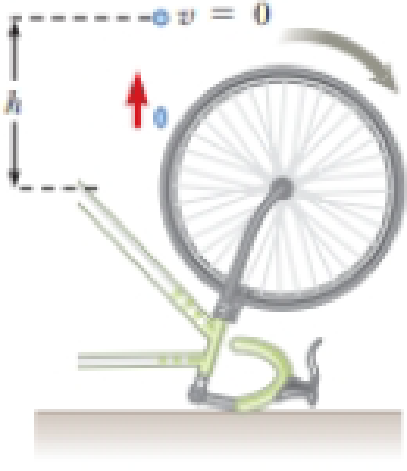
You have just bought a new bicycle. On your first riding trip, it seems that the hike comes to rest relatively quickly after you stop pedaling and let the bicycle coast on flat ground. You call the bicycle shop from which you purchased the vehicle and describe the problem. The technician says that they will replace the bearings in the wheels or do whatever else is necessary if you can prove that the frictional torque in the axle of the wheels is worse than −0.02 N · m. At first, you are discouraged by the technical sound of what you have been told and by the absence of any tool to measure torque in your garage. But then you remember that you are taking a physics class! You take your bike into the garage, turn it upside down and start spinning the wheel while you think about how to determine the frictional torque. The driveway outside the garage had a small puddle, so you notice that droplets of water are flying off the edge of one point on the tire tangentially, including drops that are projected straight upward, as shown in Figure P10.21. Ah-ha! Here is your torque-measuring method! The upward-projected drops leave the rim of the wheel at the same level as the axle. You measure the height to which a drop rises from the level of the axle: h1 = 54.0 cm. The wet spot on the tire makes one revolution and another drop is projected upward. You measure its highest point: h2 = 51.0 cm. You measure the radius of the wheel: r = 0.381 m. Finally, you take the wheel off the bike and find its mass: m = 0.850 kg. Because most of the mass of the wheel is at the tire, you model the wheel as a hoop. What do you tell the technician when you call back?
Figure P10.21
Trending nowThis is a popular solution!

Chapter 10 Solutions
Bundle: Physics For Scientists And Engineers With Modern Physics, Loose-leaf Version, 10th + Webassign Printed Access Card For Serway/jewett's Physics For Scientists And Engineers, 10th, Single-term
- I need correct answer not chatgptarrow_forwardWhat is the resistance (in (2) of a 27.5 m long piece of 17 gauge copper wire having a 1.150 mm diameter? 0.445 ΧΩarrow_forwardFind the ratio of the diameter of silver to iron wire, if they have the same resistance per unit length (as they might in household wiring). d. Ag dFe = 2.47 ×arrow_forward
- Find the ratio of the diameter of silver to iron wire, if they have the same resistance per unit length (as they might in household wiring). d Ag = 2.51 dFe ×arrow_forwardShow that the units 1 v2/Q = 1 W, as implied by the equation P = V²/R. Starting with the equation P = V²/R, we can get an expression for a watt in terms of voltage and resistance. The units for voltage, V, are equivalent to [? v2 v2 A, are equivalent to J/C ✓ X . Therefore, 1 = 1 = 1 A V1 J/s Ω V-A X = 1 W. . The units for resistance, Q, are equivalent to ? The units for current,arrow_forwardPlease solve and answer the question correctly please. Thank you!!arrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill





