MyLab Math with Pearson eText -- Standalone Access Card -- for Mathematics with Applications in the Management, Natural, and Social Sciences (12th Edition)
12th Edition
ISBN: 9780134856551
Author: Margaret L. Lial, Thomas W. Hungerford, John P. Holcomb, Bernadette Mullins
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 10, Problem 1RE
NASDAQ 100 Stocks For Exercises 1-10, the data come from a random sample of 20 companies of the NASDAQ 100 taken on June 8, 2017. (Data from: www.morningstar.com.)
For Exercises 1 and 2, (a) write a frequency distribution; (b) draw a histogram.
The variable is the price of the stock (rounded to the nearest dollar).
| 123 | 35 | 76 | 38 |
| 45 | 62 | 50 | 111 |
| 180 | 108 | 65 | 46 |
| 66 | 100 | 64 | 144 |
| 57 | 107 | 48 | 110 |
(a)
Expert Solution
To determine
Find the frequency table corresponding to the data came from a random sample of 20 companies of NASDAQ 100.
Explanation of Solution
Given:
Consider the data came from a random sample of 20 companies of NASDAQ 100
| 123 | 35 | 76 | 38 |
| 45 | 62 | 50 | 111 |
| 180 | 108 | 65 | 46 |
| 66 | 100 | 64 | 144 |
| 57 | 107 | 48 | 110 |
Calculation:
To draw the frequency table, sort the data set
35,38,45, 46,48,50,57,62,64,65,66,76,100,107,108,110,111,123,144,180
There is no repetition of data therefore the frequency of occurrence is 1 for all the data set hence the frequency distribution is
| 35 | 1 | 66 | 1 |
| 38 | 1 | 76 | 1 |
| 45 | 1 | 100 | 1 |
| 46 | 1 | 107 | 1 |
| 48 | 1 | 108 | 1 |
| 50 | 1 | 110 | 1 |
| 57 | 1 | 111 | 1 |
| 62 | 1 | 123 | 1 |
| 64 | 1 | 144 | 1 |
| 65 | 1 | 180 | 1 |
(b)
Expert Solution
To determine
To graph: Draw the histogram corresponding to the corresponding to the data came from a random sample of 20 companies of NASDAQ 100.
Explanation of Solution
Given:
Consider the data came from a random sample of 20 companies of NASDAQ 100
| 123 | 35 | 76 | 38 |
| 45 | 62 | 50 | 111 |
| 180 | 108 | 65 | 46 |
| 66 | 100 | 64 | 144 |
| 57 | 107 | 48 | 110 |
Calculation:
To draw the frequency table sort the data set
35,38,45, 46,48,50,57,62,64,65,66,76,100,107,108,110,111,123,144,180
There is no repetition of data therefore the frequency of occurrence is 1 for all the data set hence the frequency distribution is
| 35 | 1 | 66 | 1 |
| 38 | 1 | 76 | 1 |
| 45 | 1 | 100 | 1 |
| 46 | 1 | 107 | 1 |
| 48 | 1 | 108 | 1 |
| 50 | 1 | 110 | 1 |
| 57 | 1 | 111 | 1 |
| 62 | 1 | 123 | 1 |
| 64 | 1 | 144 | 1 |
| 65 | 1 | 180 | 1 |
| Range | Frequency |
| 20-40 | 2 |
| 40-60 | 5 |
| 60-80 | 5 |
| 80-100 | 0 |
| 100-120 | 5 |
| 120-140 | 1 |
| 140-160 | 1 |
| 160-180 | 0 |
| 180-200 | 1 |
The y-axis represents frequency with a scale of
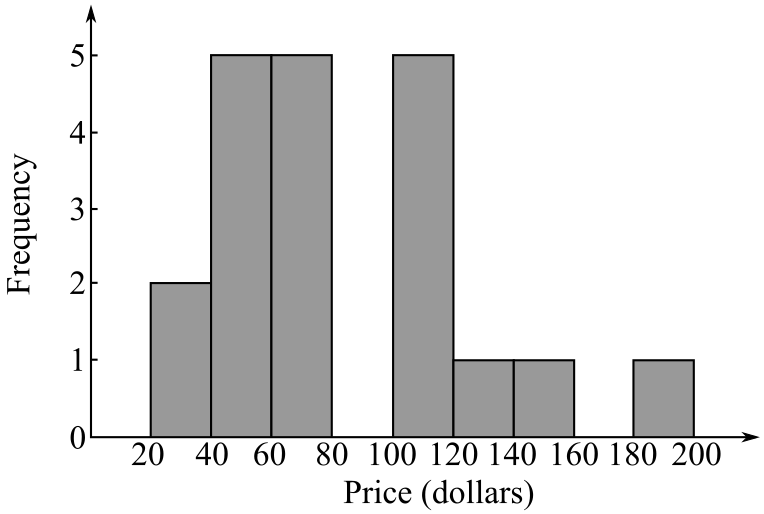
Hence, the histogram corresponding to the corresponding to the data came from a random sample of 20 companies of NASDAQ 100 is drawn.
Want to see more full solutions like this?
Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Students have asked these similar questions
Determine whether the lines
L₁ (t) = (-2,3, −1)t + (0,2,-3) and
L2 p(s) = (2, −3, 1)s + (-10, 17, -8)
intersect. If they do, find the point of intersection.
Convert the line given by the parametric equations y(t)
Enter the symmetric equations in alphabetic order.
(x(t)
= -4+6t
= 3-t
(z(t)
=
5-7t
to symmetric equations.
Find the point at which the line (t) = (4, -5,-4)+t(-2, -1,5) intersects the xy plane.
Chapter 10 Solutions
MyLab Math with Pearson eText -- Standalone Access Card -- for Mathematics with Applications in the Management, Natural, and Social Sciences (12th Edition)
Ch. 10.1 - Checkpoint 1 A restaurant trade group commissioned...Ch. 10.1 - Checkpoint 2
Make a histogram and a frequency...Ch. 10.1 - Checkpoint 3
Make a stem-and-leaf plot for the...Ch. 10.1 - Checkpoint 4
List the original data for the...Ch. 10.1 - Checkpoint 5
Characterize the shape of the...Ch. 10.1 - SP 500 Stocks The data for Exercises 1 -4 consist...Ch. 10.1 - SP 500 Stocks The data for Exercises 1 -4 consist...Ch. 10.1 - SP 500 Stocks The data for Exercises 1 -4 consist...Ch. 10.1 - SP 500 Stocks The data for Exercises 1 -4 consist...Ch. 10.1 - The data for Exercises 5-10 consist of random...
Ch. 10.1 - The data for Exercises 5-10 consist of random...Ch. 10.1 - The data for Exercises 5-10 consist of random...Ch. 10.1 - The data for Exercises 5-10 consist of random...Ch. 10.1 - The data for Exercises 5-10 consist of random...Ch. 10.1 - The data for Exercises 5-10 consist of random...Ch. 10.1 - For Exercises 11-20, construct a stem-and-leaf...Ch. 10.1 - For Exercises 11-20, construct a stem-and-leaf...Ch. 10.1 - For Exercises 11-20, construct a stem-and-leaf...Ch. 10.1 - Prob. 14ECh. 10.1 - For Exercises 11-20, construct a stem-and-leaf...Ch. 10.1 - For Exercises 11-20, construct a stem-and-leaf...Ch. 10.1 - Prob. 17ECh. 10.1 - Prob. 18ECh. 10.1 - For Exercises 11-20, construct a stem-and-leaf...Ch. 10.1 - For Exercises 11-20, construct a stem-and-leaf...Ch. 10.1 - Describe the shape of each of the given...Ch. 10.1 - Describe the shape of each of the given...Ch. 10.1 - Describe the shape of each of the given...Ch. 10.1 - Describe the shape of each of the given...Ch. 10.1 - Student Loan Defaults The following histogram...Ch. 10.1 - Stocks The following histogram shows the stock...Ch. 10.1 - Cat Ownership The stem-and-leaf plot below...Ch. 10.1 - Personal Bankruptcies The stem-and-leaf plot below...Ch. 10.1 - 29. Test Scores The grade distribution for scores...Ch. 10.1 - 30. Test Scores The grade distribution for scores...Ch. 10.2 - Checkpoint 1
Find the mean dollar amount of the...Ch. 10.2 - Checkpoint 2
Find for the following frequency...Ch. 10.2 - Checkpoint 3
Find the mean of the following...Ch. 10.2 - Checkpoint 4
Find the mean for the college tuition...Ch. 10.2 - Checkpoint 5
Find the median for the given heights...Ch. 10.2 - Checkpoint 6
Find the mode for each of the given...Ch. 10.2 - Checkpoint 7
Following is a list of the number of...Ch. 10.2 - Prob. 8CPCh. 10.2 - Prob. 1ECh. 10.2 - Prob. 2ECh. 10.2 - Prob. 3ECh. 10.2 - Prob. 4ECh. 10.2 - Prob. 5ECh. 10.2 - Prob. 6ECh. 10.2 - Prob. 7ECh. 10.2 - Prob. 8ECh. 10.2 - Prob. 9ECh. 10.2 - Prob. 10ECh. 10.2 - Prob. 11ECh. 10.2 - Prob. 12ECh. 10.2 - Prob. 13ECh. 10.2 - Prob. 14ECh. 10.2 - Find the mode or modes for each of the given lists...Ch. 10.2 - Find the mode or modes for each of the given lists...Ch. 10.2 - Find the mode or modes for each of the given lists...Ch. 10.2 - Find the mode or modes for each of the given lists...Ch. 10.2 - Find the mode or modes for each of the given lists...Ch. 10.2 - 20. When is the median the most appropriate...Ch. 10.2 - 21. When would the mode be an appropriate measure...Ch. 10.2 - Pet Ownership For Exercises 22 and 23, the...Ch. 10.2 - Pet Ownership For Exercises 22 and 23, the...Ch. 10.2 - 24. To predict the outcome of the next...Ch. 10.2 - Work each problem. (See Example 6.) MLB Payrolls...Ch. 10.2 - Work each problem. (See Example 6.) NFL Team...Ch. 10.2 - Work each problem. (See Example 6.)
27. Business...Ch. 10.2 - Work each problem. (See Example 6.) Sirius XM...Ch. 10.2 - Work each problem. (See Example 6.) Dr Pepper and...Ch. 10.2 - Natural Science The table gives the average...Ch. 10.2 - Natural Science The table gives the average...Ch. 10.2 - For Exercises 32-33 determine the shape of the...Ch. 10.2 - For Exercises 32-33 determine the shape of the...Ch. 10.2 - Prob. 34ECh. 10.2 - Prob. 35ECh. 10.2 - For Exercises 36-38, calculate the weighted...Ch. 10.2 - For Exercises 36-38, calculate the weighted...Ch. 10.2 - For Exercises 36-38, calculate the weighted...Ch. 10.2 - Prob. 39ECh. 10.2 - For Exercises 36-38, calculate the weighted...Ch. 10.3 - Checkpoint 1
Find the range for this sample of the...Ch. 10.3 - Checkpoint 2
Find the deviations from the mean for...Ch. 10.3 - Checkpoint 3
Find the standard deviation for a...Ch. 10.3 - Prob. 4CPCh. 10.3 - Prob. 1ECh. 10.3 - Prob. 2ECh. 10.3 - Prob. 3ECh. 10.3 - Prob. 4ECh. 10.3 - Prob. 5ECh. 10.3 - Prob. 6ECh. 10.3 - Prob. 7ECh. 10.3 - Finance Use the following table for Exercises...Ch. 10.3 - Finance Use the following table for Exercises...Ch. 10.3 - Prob. 10ECh. 10.3 - Education Find the standard deviation for the...Ch. 10.3 - Prob. 12ECh. 10.3 - Prob. 13ECh. 10.3 - Prob. 14ECh. 10.3 - Prob. 15ECh. 10.3 - Prob. 16ECh. 10.3 - Prob. 17ECh. 10.3 - Prob. 18ECh. 10.3 - Prob. 19ECh. 10.3 - Prob. 20ECh. 10.3 - Prob. 21ECh. 10.3 - Prob. 22ECh. 10.3 - Prob. 23ECh. 10.3 - Movie Studios' Revenue For Exercises 23-28, use...Ch. 10.3 - Prob. 25ECh. 10.3 - Prob. 26ECh. 10.3 - Prob. 27ECh. 10.3 - Prob. 28ECh. 10.3 - Prob. 29ECh. 10.3 - Prob. 30ECh. 10.3 - Prob. 34ECh. 10.3 - Prob. 31ECh. 10.3 - Prob. 32ECh. 10.3 - Prob. 33ECh. 10.3 - IBM and Microsoft Revenue The following table...Ch. 10.3 - Prob. 36ECh. 10.3 - Prob. 37ECh. 10.3 - Prob. 38ECh. 10.3 - IBM and Microsoft Revenue The following table...Ch. 10.3 - Prob. 40ECh. 10.3 - Prob. 41ECh. 10.3 - Prob. 42ECh. 10.3 - Prob. 43ECh. 10.3 - Prob. 44ECh. 10.3 - Prob. 45ECh. 10.3 - Prob. 46ECh. 10.3 - Prob. 47ECh. 10.3 - Prob. 48ECh. 10.4 - Prob. 1CPCh. 10.4 - Prob. 2CPCh. 10.4 - Prob. 3CPCh. 10.4 - Prob. 4CPCh. 10.4 - Prob. 5CPCh. 10.4 - Prob. 6CPCh. 10.4 - Prob. 7CPCh. 10.4 - 1. The peak in a normal curve occurs directly...Ch. 10.4 - Prob. 2ECh. 10.4 - Prob. 3ECh. 10.4 - Prob. 4ECh. 10.4 - Prob. 5ECh. 10.4 - Prob. 6ECh. 10.4 - Prob. 7ECh. 10.4 - Prob. 8ECh. 10.4 - Find the percentage of the total area under the...Ch. 10.4 - Prob. 10ECh. 10.4 - Prob. 11ECh. 10.4 - Prob. 12ECh. 10.4 - Prob. 13ECh. 10.4 - Prob. 14ECh. 10.4 - Prob. 15ECh. 10.4 - Prob. 16ECh. 10.4 - Prob. 17ECh. 10.4 - Prob. 18ECh. 10.4 - Prob. 19ECh. 10.4 - 20. Using Chebyshev’s theorem and the normal...Ch. 10.4 - Prob. 21ECh. 10.4 - Prob. 22ECh. 10.4 - Prob. 23ECh. 10.4 - Prob. 24ECh. 10.4 - Prob. 25ECh. 10.4 - Prob. 26ECh. 10.4 - Prob. 27ECh. 10.4 - Prob. 28ECh. 10.4 - Prob. 29ECh. 10.4 - Prob. 30ECh. 10.4 - Prob. 31ECh. 10.4 - Prob. 32ECh. 10.4 - Prob. 33ECh. 10.4 - Prob. 34ECh. 10.4 - Prob. 35ECh. 10.4 - Prob. 36ECh. 10.4 - Prob. 37ECh. 10.4 - Prob. 38ECh. 10.4 - Prob. 39ECh. 10.4 - Prob. 40ECh. 10.4 - Prob. 41ECh. 10.4 - Prob. 42ECh. 10.4 - Prob. 43ECh. 10.4 - Prob. 44ECh. 10.4 - Prob. 45ECh. 10.4 - Prob. 46ECh. 10.4 - Prob. 47ECh. 10.4 - Prob. 48ECh. 10.4 - Prob. 49ECh. 10.4 - Education The mean performance score of a large...Ch. 10.4 - Prob. 51ECh. 10.4 - Prob. 52ECh. 10.4 - Job Satisfaction According to a 2016 study...Ch. 10.4 - Prob. 54ECh. 10.4 - Prob. 55ECh. 10.4 - Prob. 56ECh. 10.4 - Prob. 57ECh. 10.4 - Prob. 58ECh. 10.4 - Student Loan Debt According to a report from the...Ch. 10.4 - Prob. 60ECh. 10.4 - Prob. 61ECh. 10.4 - Prob. 62ECh. 10 - NASDAQ 100 Stocks For Exercises 1-10, the data...Ch. 10 - Prob. 2RECh. 10 - Prob. 3RECh. 10 - Prob. 4RECh. 10 - Prob. 5RECh. 10 - Prob. 6RECh. 10 - NASDAQ 100 Stocks For Exercises 1-10, the data...Ch. 10 - Prob. 8RECh. 10 - Prob. 9RECh. 10 - Prob. 10RECh. 10 - Prob. 11RECh. 10 - Prob. 12RECh. 10 - Prob. 13RECh. 10 - Prob. 14RECh. 10 - Prob. 15RECh. 10 - Prob. 16RECh. 10 - Prob. 17RECh. 10 - Prob. 18RECh. 10 - Prob. 19RECh. 10 - Prob. 20RECh. 10 - Prob. 21RECh. 10 - Prob. 22RECh. 10 - Prob. 23RECh. 10 - Prob. 24RECh. 10 - Find the standard deviation for each of the given...Ch. 10 - Prob. 26RECh. 10 - Prob. 27RECh. 10 - Prob. 28RECh. 10 - Prob. 29RECh. 10 - Prob. 30RECh. 10 - Prob. 31RECh. 10 - Prob. 32RECh. 10 - Prob. 33RECh. 10 - Prob. 34RECh. 10 - Prob. 35RECh. 10 - Prob. 36RECh. 10 - Arm Circumference Data from a recent National...Ch. 10 - Prob. 38RECh. 10 - Prob. 39RECh. 10 - Prob. 40RECh. 10 - Prob. 41RECh. 10 - Prob. 42RECh. 10 - Prob. 43RECh. 10 - Prob. 44RECh. 10 - Prob. 45RECh. 10 - Prob. 46RECh. 10 - Prob. 47RECh. 10 - College or University Education A recent...Ch. 10 - College or University Education A recent...Ch. 10 - Prob. 50RECh. 10 - Prob. 51RECh. 10 - Prob. 52RECh. 10 - Prob. 53RECh. 10 - Prob. 54RECh. 10 - Prob. 1CECh. 10 - Prob. 2CECh. 10 - Prob. 3CECh. 10 - Prob. 4CECh. 10 - Prob. 5CECh. 10 - Prob. 6CECh. 10 - Prob. 7CECh. 10 - Prob. 8CECh. 10 - Prob. 9CECh. 10 - Prob. 10CE
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Find the distance from the point (-9, -3, 0) to the line ä(t) = (−4, 1, −1)t + (0, 1, −3) .arrow_forward1 Find a vector parallel to the line defined by the parametric equations (x(t) = -2t y(t) == 1- 9t z(t) = -1-t Additionally, find a point on the line.arrow_forwardFind the (perpendicular) distance from the line given by the parametric equations (x(t) = 5+9t y(t) = 7t = 2-9t z(t) to the point (-1, 1, −3).arrow_forward
- Let ä(t) = (3,-2,-5)t + (7,−1, 2) and (u) = (5,0, 3)u + (−3,−9,3). Find the acute angle (in degrees) between the lines:arrow_forwardNo chatgpt pls will upvotearrow_forwardA tank initially contains 50 gal of pure water. Brine containing 3 lb of salt per gallon enters the tank at 2 gal/min, and the (perfectly mixed) solution leaves the tank at 3 gal/min. Thus, the tank is empty after exactly 50 min. (a) Find the amount of salt in the tank after t minutes. (b) What is the maximum amount of salt ever in the tank?arrow_forward
- Draw a picture of a normal distribution with mean 70 and standard deviation 5.arrow_forwardWhat do you guess are the standard deviations of the two distributions in the previous example problem?arrow_forward1 What is the area of triangle ABC? 12 60° 60° A D B A 6√√3 square units B 18√3 square units 36√3 square units D 72√3 square unitsarrow_forward
- Each answer must be justified and all your work should appear. You will be marked on the quality of your explanations. You can discuss the problems with classmates, but you should write your solutions sepa- rately (meaning that you cannot copy the same solution from a joint blackboard, for exam- ple). Your work should be submitted on Moodle, before February 7 at 5 pm. 1. True or false: (a) if E is a subspace of V, then dim(E) + dim(E) = dim(V) (b) Let {i, n} be a basis of the vector space V, where v₁,..., Un are all eigen- vectors for both the matrix A and the matrix B. Then, any eigenvector of A is an eigenvector of B. Justify. 2. Apply Gram-Schmidt orthogonalization to the system of vectors {(1,2,-2), (1, −1, 4), (2, 1, 1)}. 3. Suppose P is the orthogonal projection onto a subspace E, and Q is the orthogonal projection onto the orthogonal complement E. (a) The combinations of projections P+Q and PQ correspond to well-known oper- ators. What are they? Justify your answer. (b) Show…arrow_forwardpleasd dont use chat gptarrow_forward1. True or false: (a) if E is a subspace of V, then dim(E) + dim(E+) = dim(V) (b) Let {i, n} be a basis of the vector space V, where vi,..., are all eigen- vectors for both the matrix A and the matrix B. Then, any eigenvector of A is an eigenvector of B. Justify. 2. Apply Gram-Schmidt orthogonalization to the system of vectors {(1, 2, -2), (1, −1, 4), (2, 1, 1)}. 3. Suppose P is the orthogonal projection onto a subspace E, and Q is the orthogonal projection onto the orthogonal complement E. (a) The combinations of projections P+Q and PQ correspond to well-known oper- ators. What are they? Justify your answer. (b) Show that P - Q is its own inverse. 4. Show that the Frobenius product on n x n-matrices, (A, B) = = Tr(B*A), is an inner product, where B* denotes the Hermitian adjoint of B. 5. Show that if A and B are two n x n-matrices for which {1,..., n} is a basis of eigen- vectors (for both A and B), then AB = BA. Remark: It is also true that if AB = BA, then there exists a common…arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt
The Shape of Data: Distributions: Crash Course Statistics #7; Author: CrashCourse;https://www.youtube.com/watch?v=bPFNxD3Yg6U;License: Standard YouTube License, CC-BY
Shape, Center, and Spread - Module 20.2 (Part 1); Author: Mrmathblog;https://www.youtube.com/watch?v=COaid7O_Gag;License: Standard YouTube License, CC-BY
Shape, Center and Spread; Author: Emily Murdock;https://www.youtube.com/watch?v=_YyW0DSCzpM;License: Standard Youtube License