
Concept explainers
(Complex Class) Consider class Complex shown in Figs. 10.14-10.16. The class enables operations on so-called complex numbers. These are numbers of the form real Part + imaginaryPart * i. where i has the value
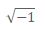
- Modify the class to enable input and output of complex numbers via overloaded >> and << operators, respectively (you should remove the toString function from the class)
- Overload the multiplication operator to enable multiplication of two complex numbers as in algebra.
- Overload the == and t = operators to allow comparisons of complex numbers.
After doing this exercise, you might want to read about the Standard Library’s complex class (from) header <comp1ex>)
- // Fig. 10.14 : Complex.h
- // Complex class definition.
- #include <string>
- #ifndef COMPLEX_H
- #define COMPLEX_H
- Class Complex {
- Public :
- Explicit Complex (double = 0.0, double = 0.0) ; // constructor
- Complex operator+(const Complex&) const; // addition
- Complex operator-(const Complex&) const; // subtraction
- Std:: string toString () const:
- Private:
- Double real : // real part
- Double imaginary ; // imaginary part
- };
- #endif
Fig. 10.14 Complex class deginition.
- // Fig. 10.15 : Complex.cpp
- // Complex class member-function definitions.
- #include <string>
- #include “Complex.h” // Complex class definition
- Using namespace std;
- // Constructor
- Complex: : Complex (double realPart, double imaginaryPart)
- : reak {real Part}, imaginary {imaginaryPart} { }
- // addition operator
- Complex Complex : : operator+ (const Complex& operand2) const {
- Return Complex {real +operand2. Real, imaginary+ operand2. Imaginary};
- }
- // subtraction operator
- Complex Complex : : operator-(const Complex& opetand2) const {
- Return Complex { real − operand 2.real, imaginary − operand2. Imaginary } :
- }
- // return string representation of a complex object in the form: (a, b)
- String Complex : : to String () const {
- Return “(“s +to_string(real) + “, “s + to_string(imaginary) + “)”s;
- }
Fig.10.15 Complex class member-function definition
25 // Fig. 10.16; fig10_16.cpp
26 // Complex class test program.
27 #include <iostream>
28 #include “Complex.h”
29 using namespace std;
30
31 int main () {
32 Complex x:
33 Complex y {4.3, 8,2}:
34 Complex z {3,3, 1,1}:
35
36 count << “x: “ << x.toString () << :\ny: “<<y.to string ()
37 << “\nz: “ <<z:
38
39 x=y+z;
40 count << “\n\nx = y+z:\n” << x.toString () << “= “ << y.toString()
41 << “ + ” <<z.toString ():
42
43 x = y - z :
44 count << “\n\nx = y-z:\n” << x. to String () << “ = “ << y. to String ()
45 << “ - “ << z. toString () << end}:
X: (0, 0)
Y: (4,3, 8,2)
Z: (3,3, 1.1)
X = y+z:
(7.6, 9.3) = (4.3, 8.2) + (3.3, 1.1)
X= y-z :
(1, 7.1) = (4.3, 8.2 ) −(3.3, 1.1)
Fig. 10.16 Complex class test program (Part 2 of 2)
Want to see the full answer?
Check out a sample textbook solution
Chapter 10 Solutions
C++ How to Program (Early Objects Version)
- using r language for integration theta = integral 0 to infinity (x^4)*e^(-x^2)/2 dx (1) use the density function of standard normal distribution N(0,1) f(x) = 1/sqrt(2pi) * e^(-x^2)/2 -infinity <x<infinity as importance function and obtain an estimate theta 1 for theta set m=100 for the estimate whatt is the estimate theta 1? (2)use the density function of gamma (r=5 λ=1/2)distribution f(x)=λ^r/Γ(r) x^(r-1)e^(-λx) x>=0 as importance function and obtain an estimate theta 2 for theta set m=1000 fir the estimate what is the estimate theta2? (3) use simulation (repeat 1000 times) to estimate the variance of the estimates theta1 and theta 2 which one has smaller variance?arrow_forwardusing r language A continuous random variable X has density function f(x)=1/56(3x^2+4x^3+5x^4).0<=x<=2 (1) secify the density g of the random variable Y you find for the acceptance rejection method. (2) what is the value of c you choose to use for the acceptance rejection method (3) use the acceptance rejection method to generate a random sample of size 1000 from the distribution of X .graph the density histogram of the sample and compare it with the density function f(x)arrow_forwardusing r language a continuous random variable X has density function f(x)=1/4x^3e^-(pi/2)^4,x>=0 derive the probability inverse transformation F^(-1)x where F(x) is the cdf of the random variable Xarrow_forward
- using r language in an accelerated failure test, components are operated under extreme conditions so that a substantial number will fail in a rather short time. in such a test involving two types of microships 600 chips manufactured by an existing process were tested and 125 of them failed then 800 chips manufactured by a new process were tested and 130 of them failed what is the 90%confidence interval for the difference between the proportions of failure for chips manufactured by two processes? using r languagearrow_forwardI want a picture of the tools and the pictures used Cisco Packet Tracer Smart Home Automation:o Connect a temperature sensor and a fan to a home gateway.o Configure the home gateway so that the fan is activated when the temperature exceedsa set threshold (e.g., 30°C).2. WiFi Network Configuration:o Set up a wireless LAN with a unique SSID.o Enable WPA2 encryption to secure the WiFi network.o Implement MAC address filtering to allow only specific clients to connect.3. WLC Configuration:o Deploy at least two wireless access points connected to a Wireless LAN Controller(WLC).o Configure the WLC to manage the APs, broadcast the configured SSID, and applyconsistent security settings across all APs.arrow_forwardA. What will be printed executing the code above?B. What is the simplest way to set a variable of the class Full_Date to January 26 2020?C. Are there any empty constructors in this class Full_Date?a. If there is(are) in which code line(s)?b. If there is not, how would an empty constructor be? (create the code lines for it)D. Can the command std::cout << d1.m << std::endl; be included after line 28 withoutcausing an error?a. If it can, what will be printed?b. If it cannot, how could this command be fixed?arrow_forward
- Cisco Packet Tracer Smart Home Automation:o Connect a temperature sensor and a fan to a home gateway.o Configure the home gateway so that the fan is activated when the temperature exceedsa set threshold (e.g., 30°C).2. WiFi Network Configuration:o Set up a wireless LAN with a unique SSID.o Enable WPA2 encryption to secure the WiFi network.o Implement MAC address filtering to allow only specific clients to connect.3. WLC Configuration:o Deploy at least two wireless access points connected to a Wireless LAN Controller(WLC).o Configure the WLC to manage the APs, broadcast the configured SSID, and applyconsistent security settings across all APs.arrow_forwardTransform the TM below that accepts words over the alphabet Σ= {a, b} with an even number of a's and b's in order that the output tape head is positioned over the first letter of the input, if the word is accepted, and all letters a should be replaced by the letter x. For example, for the input aabbaa the tape and head at the end should be: [x]xbbxx z/z,R b/b,R F ① a/a,R b/b,R a/a, R a/a,R b/b.R K a/a,R L b/b,Rarrow_forwardGiven the C++ code below, create a TM that performs the same operation, i.e., given an input over the alphabet Σ= {a, b} it prints the number of letters b in binary. 1 #include 2 #include 3 4- int main() { std::cout > str; for (char c : str) { if (c == 'b') count++; 5 std::string str; 6 int count = 0; 7 char buffer [1000]; 8 9 10 11- 12 13 14 } 15 16- 17 18 19 } 20 21 22} std::string binary while (count > 0) { binary = std::to_string(count % 2) + binary; count /= 2; std::cout << binary << std::endl; return 0;arrow_forward
- Considering the CFG described below, answer the following questions. Σ = {a, b} • NT = {S} Productions: P1 S⇒aSa P2 P3 SbSb S⇒ a P4 S⇒ b A. List one sequence of productions that can accept the word abaaaba; B. Give three 5-letter words that can be accepted by this CFG; C. Create a Pushdown automaton capable of accepting the language accepted by this CFG.arrow_forwardGiven the FSA below, answer the following questions. b 1 3 a a b b с 2 A. Write a RegEx that is equivalent to this FSA as it is; B. Write a RegEx that is equivalent to this FSA removing the states and edges corresponding to the letter c. Note: To both items feel free to use any method you want, including analyzing which words are accepted by the FSA, to generate your RegEx.arrow_forward3) Finite State Automata Given the FSA below, answer the following questions. a b a b 0 1 2 b b 3 A. Give three 4-letter words that can be accepted by this FSA; B. Give three 4-letter words that cannot be accepted by this FSA; C. How could you describe the words accepted by this FSA? D. Is this FSA deterministic or non-deterministic?arrow_forward
 C++ Programming: From Problem Analysis to Program...Computer ScienceISBN:9781337102087Author:D. S. MalikPublisher:Cengage Learning
C++ Programming: From Problem Analysis to Program...Computer ScienceISBN:9781337102087Author:D. S. MalikPublisher:Cengage Learning C++ for Engineers and ScientistsComputer ScienceISBN:9781133187844Author:Bronson, Gary J.Publisher:Course Technology Ptr
C++ for Engineers and ScientistsComputer ScienceISBN:9781133187844Author:Bronson, Gary J.Publisher:Course Technology Ptr

