
(a)
To make: a Venn diagram with information and consider options when labeling the diagram.
(a)
Answer to Problem 10.8AYK
The Venn diagram was constructed.
Explanation of Solution
Given:
An African study tested 543 children for the sickle-cell anemia trait and for malaria infection. Of those tested, 25% had sickle-cell, 34.6% had malaria and 6.6% had both sickle cell and malaria.
Calculation:
Based on this information a Venn diagram can be constructed. To do this, the probabilities of both malaria and not sickle-cell and sickle-cell and not malaria need to be calculated as follows:
To calculate the
From this, the probability that a child has neither sickle cell nor malaria can be calculated by taking 1 minus this above calculated value.
These values can now be used to complete the Venn diagram.
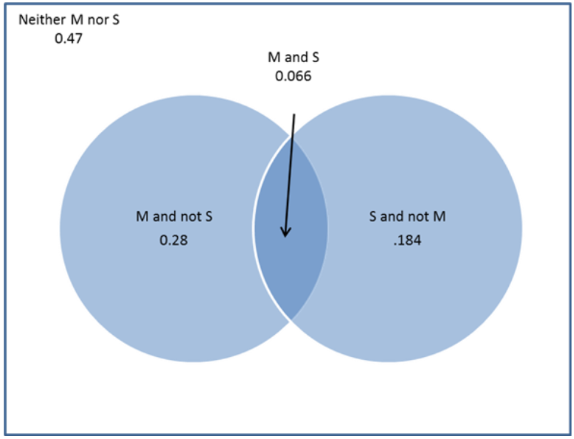
Conclusion:
Therefore, the Venn diagram was constructed.
(b)
To find: the probability that a given child has either malaria or the sickle-cell trait.
(b)
Answer to Problem 10.8AYK
The probability that a child has either malaria or sickle cell is 0.53.
Explanation of Solution
Calculation:
The probability that a given child has neither malaria nor sickle cell can be seen in the Venn diagram. In addition, to calculate the probability that a child has neither sickle cell nor malaria, first the probability a child has either sickle cell or malaria needs to be determined.
From this, the probability that a child has neither sickle cell nor malaria can be calculated by taking 1 minus this value.
The probability that a child has neither sickle cell nor malaria is 0.47.
Also, the probability that a child has either malaria or sickle cell can be determined using the given information. To do this, the probability that a child has sickle cell is added to the probability that a child has malaria. This value is then subtracted from the probability that a child has both.
Conclusion:
Therefore,the probability that a child has either malaria or sickle cell is 0.53.
(c)
To find: the probability that a given child has malaria, given that the child has the sickle-cell trait.
(c)
Answer to Problem 10.8AYK
The probability that a child has malaria given they do not have sickle cell is 0.373.
Explanation of Solution
Calculation:
The probability that a child has malaria given that a child has sickle cell is expressed as follows:
The probability that a child has malaria given they have sickle cell is 0.264.
The probability that a child has malaria given that they do not have sickle cell is expressed as follows:
First, the probability that a child does not have sickle cell needs to be determined by taking 1 minus the probability that a child has sickle cell (0.25).
Next, substitute the values into the formula given above.
Conclusion:
Therefore,the probability that a child has malaria given they do not have sickle cell is 0.373.
(d)
To describe: the
(d)
Answer to Problem 10.8AYK
Therefore, the probability of malaria and sickle cell using the multiplication rule gives a probability of 0.0865.As a result, these two events are not independent.
Explanation of Solution
Calculation:
To verify independence, the multiplication of the probabilities of malaria and sickle cell should be equal to the probability of malaria and sickle cell, which is 0.066.
Calculating the probability of malaria and sickle cell using the multiplication rule gives a probability of 0.0865. This is greater than and does not match the probability of both malaria and sickle cell of 0.066 as given in the example. As a result, these two events are not independent.
Conclusion:
Therefore, the probability of malaria and sickle cell using the multiplication rule gives a probability of 0.0865.As a result, these two events are not independent.
Want to see more full solutions like this?
Chapter 10 Solutions
Practice of Statistics in the Life Sciences
- Let X be a random variable with support SX = {−3, 0.5, 3, −2.5, 3.5}. Part ofits probability mass function (PMF) is given bypX(−3) = 0.15, pX(−2.5) = 0.3, pX(3) = 0.2, pX(3.5) = 0.15.(a) Find pX(0.5).(b) Find the cumulative distribution function (CDF), FX(x), of X.1(c) Sketch the graph of FX(x).arrow_forwardA well-known company predominantly makes flat pack furniture for students. Variability with the automated machinery means the wood components are cut with a standard deviation in length of 0.45 mm. After they are cut the components are measured. If their length is more than 1.2 mm from the required length, the components are rejected. a) Calculate the percentage of components that get rejected. b) In a manufacturing run of 1000 units, how many are expected to be rejected? c) The company wishes to install more accurate equipment in order to reduce the rejection rate by one-half, using the same ±1.2mm rejection criterion. Calculate the maximum acceptable standard deviation of the new process.arrow_forward5. Let X and Y be independent random variables and let the superscripts denote symmetrization (recall Sect. 3.6). Show that (X + Y) X+ys.arrow_forward
- 8. Suppose that the moments of the random variable X are constant, that is, suppose that EX" =c for all n ≥ 1, for some constant c. Find the distribution of X.arrow_forward9. The concentration function of a random variable X is defined as Qx(h) = sup P(x ≤ X ≤x+h), h>0. Show that, if X and Y are independent random variables, then Qx+y (h) min{Qx(h). Qr (h)).arrow_forward10. Prove that, if (t)=1+0(12) as asf->> O is a characteristic function, then p = 1.arrow_forward
- 9. The concentration function of a random variable X is defined as Qx(h) sup P(x ≤x≤x+h), h>0. (b) Is it true that Qx(ah) =aQx (h)?arrow_forward3. Let X1, X2,..., X, be independent, Exp(1)-distributed random variables, and set V₁₁ = max Xk and W₁ = X₁+x+x+ Isk≤narrow_forward7. Consider the function (t)=(1+|t|)e, ER. (a) Prove that is a characteristic function. (b) Prove that the corresponding distribution is absolutely continuous. (c) Prove, departing from itself, that the distribution has finite mean and variance. (d) Prove, without computation, that the mean equals 0. (e) Compute the density.arrow_forward
- 1. Show, by using characteristic, or moment generating functions, that if fx(x) = ½ex, -∞0 < x < ∞, then XY₁ - Y2, where Y₁ and Y2 are independent, exponentially distributed random variables.arrow_forward1. Show, by using characteristic, or moment generating functions, that if 1 fx(x): x) = ½exarrow_forward1990) 02-02 50% mesob berceus +7 What's the probability of getting more than 1 head on 10 flips of a fair coin?arrow_forward
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman





