
Concept explainers
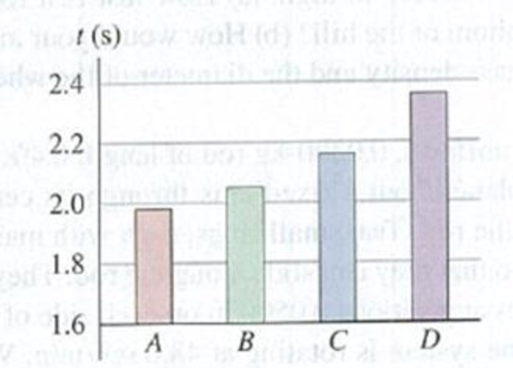
DATA You have one object of each of these shapes, all with mass 0.840 kg: a uniform solid cylinder, a thin-walled hollow cylinder, a uniform solid sphere, and a thin-walled hollow sphere. You release each object from rest at the same vertical height h above the bottom of a long wooden ramp that is inclined at 35.0° from the horizontal. Each object rolls without slipping down the ramp. You measure the time t that it takes each one to reach the bottom of the ramp; Fig. P10.89 shows the results, (a) From the bar graphs, identify objects A through D by shape, (b) Which of objects A through D has the greatest total kinetic energy at the bottom of the ramp, or do all have the same kinetic energy? (c) Which of objects A through D has the greatest rotational kinetic energy
Figure P10.89
Learn your wayIncludes step-by-step video

Chapter 10 Solutions
University Physics with Modern Physics (14th Edition)
Additional Science Textbook Solutions
Laboratory Experiments in Microbiology (12th Edition) (What's New in Microbiology)
Human Biology: Concepts and Current Issues (8th Edition)
Campbell Essential Biology with Physiology (5th Edition)
Chemistry: Structure and Properties (2nd Edition)
Organic Chemistry (8th Edition)
Microbiology: An Introduction
- A small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius cc and outer radius d (Figure 1). The inner shell has total charge +2q, and the outer shell has charge −2q. What is the direction of the electric field for b<r<c? Calculate the magnitude of the electric field for c<r<d. Calculate the magnitude of the electric field for r>d.arrow_forwardTICE D Conservation of Momentum 1. A 63.0 kg astronaut is on a spacewalk when the tether line to the shuttle breaks. The astronaut is able to throw a spare 10.0 kg oxygen tank in a direction away from the shuttle with a speed of 12.0 m/s, propelling the astronaut back to the shuttle. Assuming that the astronaut starts from rest with respect to the shuttle, find the astronaut's final speed with respect to the shuttle after the tank is thrown. 2. An 85.0 kg fisherman jumps from a dock into a 135.0 kg rowboat at rest on the west side of the dock. If the velocity of the fisherman is 4.30 m/s to the west as he leaves the dock, what is the final velocity of the fisher- man and the boat? 3. Each croquet ball in a set has a mass of 0.50 kg. The green ball, traveling at 12.0 m/s, strikes the blue ball, which is at rest. Assuming that the balls slide on a frictionless surface and all collisions are head-on, find the final speed of the blue ball in each of the following situations: a. The green…arrow_forwardThe 5.15 A current through a 1.50 H inductor is dissipated by a 2.15 Q resistor in a circuit like that in the figure below with the switch in position 2. 0.632/ C A L (a) 0.368/ 0+ 0 = L/R 2T 3r 4 (b) (a) What is the initial energy (in J) in the inductor? 0 t = L/R 2t (c) Эт 4t 19.89 ] (b) How long will it take (in s) the current to decline to 5.00% of its initial value? 2.09 S (c) Calculate the average power (in W) dissipated, and compare it with the initial power dissipated by the resistor. 28.5 1.96 x W X (ratio of initial power to average power)arrow_forward
- Imagine a planet where gravity mysteriously acts tangent to the equator and in the eastward directioninstead of radially inward. Would this force do work on an object moving on the earth? What is the sign ofthe work, and does it depend on the path taken? Explain by using the work integral and provide a sketch ofthe force and displacement vectors. Provide quantitative examples.arrow_forwardIf a force does zero net work on an object over a closed loop, does that guarantee the force is conservative? Explain with an example or counterexamplearrow_forwardA futuristic amusement ride spins riders in a horizontal circle of radius 5 m at a constant speed. Thefloor drops away, leaving riders pinned to the wall by friction (coefficient µ = 0.4). What minimum speedensures they don’t slip, given g = 10 m/s²? Draw diagram (or a few) showing all forces, thevelocity of the rider, and their accelerationarrow_forward
- Your RL circuit has a characteristic time constant of 19.5 ns, and a resistance of 4.60 MQ. (a) What is the inductance (in H) of the circuit? 0.00897 × H (b) What resistance (in MQ) should you use (instead of the 4.60 MQ resistor) to obtain a 1.00 ns time constant, perhaps needed for quick response in an oscilloscope? 8.97 * ΜΩarrow_forwardYour RL circuit has a characteristic time constant of 19.5 ns, and a resistance of 4.60 MQ. (a) What is the inductance (in H) of the circuit? H (b) What resistance (in MQ) should you use (instead of the 4.60 MQ resistor) to obtain a 1.00 ns time constant, perhaps needed for quick response in an oscilloscope? ΜΩarrow_forwardAt a distance of 0.212 cm from the center of a charged conducting sphere with radius 0.100cm, the electric field is 485 N/C . What is the electric field 0.598 cm from the center of the sphere? At a distance of 0.196 cmcm from the axis of a very long charged conducting cylinder with radius 0.100cm, the electric field is 485 N/C . What is the electric field 0.620 cm from the axis of the cylinder? At a distance of 0.202 cm from a large uniform sheet of charge, the electric field is 485 N/C . What is the electric field 1.21 cm from the sheet?arrow_forward
- A hollow, conducting sphere with an outer radius of 0.260 m and an inner radius of 0.200 m has a uniform surface charge density of +6.67 × 10−6 C/m2. A charge of -0.800 μC is now introduced into the cavity inside the sphere. What is the new charge density on the outside of the sphere? Calculate the strength of the electric field just outside the sphere. What is the electric flux through a spherical surface just inside the inner surface of the sphere?arrow_forwardA point charge of -3.00 μC is located in the center of a spherical cavity of radius 6.60 cm inside an insulating spherical charged solid. The charge density in the solid is 7.35 × 10−4 C/m3. Calculate the magnitude of the electric field inside the solid at a distance of 9.10 cm from the center of the cavity. Find the direction of this electric field.arrow_forwardAn infinitely long conducting cylindrical rod with a positive charge λ per unit length is surrounded by a conducting cylindrical shell (which is also infinitely long) with a charge per unit length of −2λ and radius r1, as shown in the figure. What is E(r), the radial component of the electric field between the rod and cylindrical shell as a function of the distance r from the axis of the cylindrical rod? Express your answer in terms of λ, r, and ϵ0, the permittivity of free space. What is σinner, the surface charge density (charge per unit area) on the inner surface of the conducting shell? What is σouterσouter, the surface charge density on the outside of the conducting shell? (Recall from the problem statement that the conducting shell has a total charge per unit length given by −2λ.) What is the radial component of the electric field, E(r), outside the shell?arrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





