Chapter 10, Problem 10.6CP

<

To determine

(a)

To compute:

The flow rate follows from the sluice gate correlation Q.

Answer to Problem 10.6CP

The flow rate follows from the sluice gate correlation $Q=379f{t}^3/s.$

Explanation of Solution

Figure:

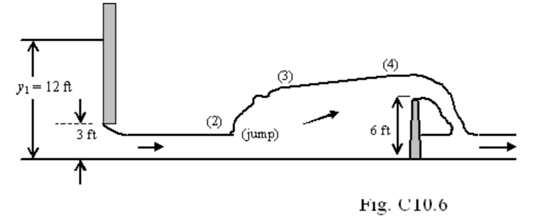
Given:

$b=8ft$, $H=3ft$, $y_1=12ft$, $g=32.2ft/s^2.$

Concept Used:

Annuity problem requires the use of the formula as follows:

$Q=C_{d}Hb\sqrt{2g{y}_1}$

$\Rightarrow$

$C_d=\frac{0.61}{\sqrt{1+0.61\left(\frac{H_1}{y_1}\right)}}$

Here,

Acceleration gravity $=g$, height $=H$, width $=b.$

Calculation:

As per the given problem:

$b=8ft$, $H=3ft$

Annuity problem requires the use of this formula:

$C_d=\frac{0.61}{\sqrt{1+0.61\left(\frac{H_1}{y_1}\right)}}$

Substitute these values in the formula

$C_d=\frac{0.61}{\sqrt{1+0.61\left(\frac{3ft}{12ft}\right)}}=0.568$

$C_d=0.568$

Annuity problem requires the use of this formula:

$C_d=0.568$, $b=8ft$, $H=3ft$, $y_1=12ft$, $g=32.2ft/s^2$

$Q=C_{d}Hb\sqrt{2g{y}_1}$

Substitute these values in the formula:

$Q=\left(0.568\right)\left(3ft\right)\left(8ft\right)\sqrt{2\left(32.2ft/s^2\right)\left(12ft\right)}=379f{t}^3/s$

$Q=379f{t}^3/s$

Conclusion:

The flow rate follows from the sluice gate correlation $Q=379f{t}^3/s.$.

<

To determine

(b)

To compute:

The normal depth.

Answer to Problem 10.6CP

It has no normal depth.

Explanation of Solution

Given Information:

This channel is horizontal.

If you know the flow rate, you can find the normal depth, but this channel is horizontal, It has no normal depth.

Conclusion:

It has no normal depth.

<

To determine

(c)

To compute:

$\left(y_2\right)$.

$y_2=1.83ft$

Given:

$Q=379f{t}^3/s$, $b=8ft$, $g=32.2ft/s^2$, $y_1=12ft$

Concept Used:

Annuity problem requires the use of the formula as follows:

$E_1=y_1+\frac{V_1{}^2}{2g}$

$E_2=y_2+\frac{V_2{}^2}{2g}$

Annuity problem requires the use of the formula as follows:

$\frac{Q}{b}=V_1{y}_1$

$\frac{Q}{b}=V_2{y}_2$

Here,

Velocity $=V$, Depth $=y$, Flow rate $=Q$

Annuity problem requires the use of the formula as follows

$F{r}_2=\frac{V_2}{\sqrt{g{y}_2}}$

Calculation:

As per the given problem:

$Q=379f{t}^3/s$, $b=8ft$, $g=32.2ft/s^2$, $y_1=12ft$

Annuity problem requires the use of this formula:

$\frac{Q}{b}=V_1{y}_1$

Substitute these values in the formula:

$\frac{Q}{b}=\frac{379f{t}^3}{8ft}=47.39f{t}^2/s$

$\Rightarrow$

$47.39f{t}^2/s=V_1{y}_1$

$\Rightarrow$

$V_1=47.39f{t}^2/s\left(12ft\right)=3.95ft/s$

$V_1=3.95ft/s$

Annuity problem requires the use of this formula:

$V_1=3.95ft/s$, $y_1=12ft$, $g=32.2ft/s^2$

$E_1=y_1+\frac{V_1{}^2}{2g}$

Substitute these values in the formula:

$E_1=12ft+\frac{{\left(3.95ft/s\right)}^2}{2\left(32.2ft/s^2\right)}=12.24ft$

$E_1=12.24ft$

According to Bernoulli equation:

$E_1=E_2$

$E_2=12.24ft$

Annuity problem requires the use of this formula:

$\frac{Q}{b}=47.39f{t}^2/s$, $E_2=12.24ft$, $g=32.2ft/s^2.$

$\frac{Q}{b}=V_2{y}_2.$

Substitute these values in the formula:

$V_2=\frac{47.39f{t}^2/s}{y_2}$

Annuity problem requires the use of this formula:

$E_2=y_2+\frac{V_2{}^2}{2g}$

Substitute these values in the formula:

$\Rightarrow$

$12.24ft=y_2+\frac{{\left(\frac{47.39f{t}^2/s}{y_2}\right)}^2}{2\left(32.2ft/s^2\right)}$

$y_2=1.83ft$

Conclusion:

$y_2=1.83ft$.

Answer to Problem 10.6CP

$y_2=1.83ft$

Explanation of Solution

Given:

$Q=379f{t}^3/s$, $b=8ft$, $g=32.2ft/s^2$, $y_1=12ft$

Concept Used:

Annuity problem requires the use of the formula as follows:

$E_1=y_1+\frac{V_1{}^2}{2g}$

$E_2=y_2+\frac{V_2{}^2}{2g}$

Annuity problem requires the use of the formula as follows:

$\frac{Q}{b}=V_1{y}_1$

$\frac{Q}{b}=V_2{y}_2$

Here,

Velocity $=V$, Depth $=y$, Flow rate $=Q$

Annuity problem requires the use of the formula as follows

$F{r}_2=\frac{V_2}{\sqrt{g{y}_2}}$

Calculation:

As per the given problem:

$Q=379f{t}^3/s$, $b=8ft$, $g=32.2ft/s^2$, $y_1=12ft$

Annuity problem requires the use of this formula:

$\frac{Q}{b}=V_1{y}_1$

Substitute these values in the formula:

$\frac{Q}{b}=\frac{379f{t}^3}{8ft}=47.39f{t}^2/s$

$\Rightarrow$

$47.39f{t}^2/s=V_1{y}_1$

$\Rightarrow$

$V_1=47.39f{t}^2/s\left(12ft\right)=3.95ft/s$

$V_1=3.95ft/s$

Annuity problem requires the use of this formula:

$V_1=3.95ft/s$, $y_1=12ft$, $g=32.2ft/s^2$

$E_1=y_1+\frac{V_1{}^2}{2g}$

Substitute these values in the formula:

$E_1=12ft+\frac{{\left(3.95ft/s\right)}^2}{2\left(32.2ft/s^2\right)}=12.24ft$

$E_1=12.24ft$

According to Bernoulli equation:

$E_1=E_2$

$E_2=12.24ft$

Annuity problem requires the use of this formula:

$\frac{Q}{b}=47.39f{t}^2/s$, $E_2=12.24ft$, $g=32.2ft/s^2.$

$\frac{Q}{b}=V_2{y}_2.$

Substitute these values in the formula:

$V_2=\frac{47.39f{t}^2/s}{y_2}$

Annuity problem requires the use of this formula:

$E_2=y_2+\frac{V_2{}^2}{2g}$

Substitute these values in the formula:

$\Rightarrow$

$12.24ft=y_2+\frac{{\left(\frac{47.39f{t}^2/s}{y_2}\right)}^2}{2\left(32.2ft/s^2\right)}$

$y_2=1.83ft$

Conclusion:

$y_2=1.83ft$.

<

To determine

(d)

To compute:

$\left(y_3\right)$.

$y_3=7.86ft$

Given:

$y_2=1.83ft$, $V_2=\frac{47.39f{t}^2/s}{y_2}$

Calculation:

Annuity problem requires the use of this formula:

$V_2=\frac{47.39f{t}^2/s}{y_2}$

Substitute these values in the formula:

$V_2=\frac{47.39f{t}^2/s}{1.83ft}=25.9ft/s$

$V_2=25.9ft/s$

Annuity problem requires the use of this formula:

$V_2=25.9ft/s$, $g=32.2ft/s^2$, $y_2=1.83ft$

$F{r}_2=\frac{V_2}{\sqrt{g{y}_2}}$

Substitute these values in the formula:

$F{r}_2=\frac{25.9}{\sqrt{\left(32.2\right)1.83}}=3.37$

$F{r}_2=3.37$

The flow in section 2 is highly supercritical, Now use hydraulic jump theory

Annuity problem requires the use hydraulic jump theory as follow:

$F{r}_2=3.37$, $y_2=1.83ft$

$\frac{2y_3}{y_2}=-1+\sqrt{1+8F{r}_2{}^2}$

Substitute these values in the formula:

$\frac{2y_3}{\left(1.83\right)}=-1+\sqrt{1+8{\left(3.37\right)}^2}$

$\Rightarrow$

$y_3=7.86ft$

Conclusion:

$y_3=7.86ft$.

Answer to Problem 10.6CP

$y_3=7.86ft$

Explanation of Solution

Given:

$y_2=1.83ft$, $V_2=\frac{47.39f{t}^2/s}{y_2}$

Calculation:

Annuity problem requires the use of this formula:

$V_2=\frac{47.39f{t}^2/s}{y_2}$

Substitute these values in the formula:

$V_2=\frac{47.39f{t}^2/s}{1.83ft}=25.9ft/s$

$V_2=25.9ft/s$

Annuity problem requires the use of this formula:

$V_2=25.9ft/s$, $g=32.2ft/s^2$, $y_2=1.83ft$

$F{r}_2=\frac{V_2}{\sqrt{g{y}_2}}$

Substitute these values in the formula:

$F{r}_2=\frac{25.9}{\sqrt{\left(32.2\right)1.83}}=3.37$

$F{r}_2=3.37$

The flow in section 2 is highly supercritical, Now use hydraulic jump theory

Annuity problem requires the use hydraulic jump theory as follow:

$F{r}_2=3.37$, $y_2=1.83ft$

$\frac{2y_3}{y_2}=-1+\sqrt{1+8F{r}_2{}^2}$

Substitute these values in the formula:

$\frac{2y_3}{\left(1.83\right)}=-1+\sqrt{1+8{\left(3.37\right)}^2}$

$\Rightarrow$

$y_3=7.86ft$

Conclusion:

$y_3=7.86ft$.

<

To determine

(e)

To compute:

$\left(y_4\right).$.

$\left(y_4\right)=11.53ft$

Given:

Calculation:

$y_{weir}=6ft$, $Q=379f{t}^3/s$, $g=32.2ft/s^2$ s Annuity problem requires the use of this formula:

$C_{d,shape-crested}=0.564+0.0846\frac{H_4}{Y_{weir}}$

Substitute these values in the formula:

$C_{d,shape-crested}=0.564+0.0846\frac{H_4}{6ft}$

Annuity problem requires the use of this formula:

$Q=379f{t}^3/s$, $C_{d,shape-crested}=0.564+0.0846\frac{H_4}{6ft}$, $g=32.2ft/s^2$

$Q=C_{d}b\sqrt{g}{H}_4{}^{3/2}$

Substitute these values in the formula:

$Q=\left(0.564+0.0846\frac{H_4}{6ft}\right)\left(8ft\right)\sqrt{\left(32.2ft/s^2\right)}{H}_4{}^{3/2}$

$379f{t}^3/s=\left(0.564+0.0846\frac{H_4}{6ft}\right)\left(8ft\right)\sqrt{\left(32.2ft/s^2\right)}{H}_4{}^{3/2}$

$H_4=5.53ft$

Annuity problem requires the use of this formula:

$H_4=5.53ft$

$C_{d,shape-crested}=0.564+0.0846\frac{H_4}{6ft}$

Substitute these values in the formula

$C_{d,shape-crested}=0.564+0.0846\frac{5.53}{6ft}=0.642$

$C_d=0.642$

Annuity problem requires the use of this formula

$\left(y_4\right)=H_4+Y_{weir}$

Substitute these values in the formula:

$\left(y_4\right)=5.53+6ft=11.53ft$

$\left(y_4\right)=11.53ft$

Conclusion:

$\left(y_4\right)=11.53ft$.

Answer to Problem 10.6CP

$\left(y_4\right)=11.53ft$

Explanation of Solution

Given:

Calculation:

$y_{weir}=6ft$, $Q=379f{t}^3/s$, $g=32.2ft/s^2$ s Annuity problem requires the use of this formula:

$C_{d,shape-crested}=0.564+0.0846\frac{H_4}{Y_{weir}}$

Substitute these values in the formula:

$C_{d,shape-crested}=0.564+0.0846\frac{H_4}{6ft}$

Annuity problem requires the use of this formula:

$Q=379f{t}^3/s$, $C_{d,shape-crested}=0.564+0.0846\frac{H_4}{6ft}$, $g=32.2ft/s^2$

$Q=C_{d}b\sqrt{g}{H}_4{}^{3/2}$

Substitute these values in the formula:

$Q=\left(0.564+0.0846\frac{H_4}{6ft}\right)\left(8ft\right)\sqrt{\left(32.2ft/s^2\right)}{H}_4{}^{3/2}$

$379f{t}^3/s=\left(0.564+0.0846\frac{H_4}{6ft}\right)\left(8ft\right)\sqrt{\left(32.2ft/s^2\right)}{H}_4{}^{3/2}$

$H_4=5.53ft$

Annuity problem requires the use of this formula:

$H_4=5.53ft$

$C_{d,shape-crested}=0.564+0.0846\frac{H_4}{6ft}$

Substitute these values in the formula

$C_{d,shape-crested}=0.564+0.0846\frac{5.53}{6ft}=0.642$

$C_d=0.642$

Annuity problem requires the use of this formula

$\left(y_4\right)=H_4+Y_{weir}$

Substitute these values in the formula:

$\left(y_4\right)=5.53+6ft=11.53ft$

$\left(y_4\right)=11.53ft$

Conclusion:

$\left(y_4\right)=11.53ft$.